Перейти к:
Анализ изменения напряженно-деформированного состояния и проницаемости терригенного коллектора на основе численной модели околоскважинной зоны с элементами крепи и перфорационными каналами
https://doi.org/10.18599/grs.2024.4.6
Аннотация
Разработана конечно-элементная схема, включающая участок породы-коллектора, цементный камень, обсадную колонну и перфорационные каналы. Отмечено, что для исключения возникновения концентраторов напряжений на контактах обсадная колонна – цементный камень и цементный камень – горная порода в численной модели заданы контактные элементы, за счет этого происходит «скольжение» конструктивных элементов, но в то же время осуществляется достоверное перераспределение напряжений. Выполнено численное моделирование напряженного состояния околоскважиной зоны с использованием разработанной модели при изменяющейся депрессии на представленный терригенным коллектором пласт одного из нефтяных месторождений Пермского края. Показано, что запас прочности колонны составляет порядка 3–4 ед., исключение составляют небольшие участки вблизи верхней и нижней областей перфорационных отверстий, на которых этот показатель близок к единице. Для цементного камня запас прочности составил 2–3 ед., однако отмечены участки с наименьшим значением (1,35), также сконцентрированные вблизи перфорационных каналов. Для анализа изменения проницаемости бралась зависимость рассматриваемой характеристики от эффективных напряжений, установлено, что в верхней и нижней частях перфорационных отверстий имеются зоны пониженных напряжений и увеличения проницаемости до 20% от исходного значения. с увеличением депрессии на пласт происходит снижение проницаемости на боковых участках перфорационных отверстий вертикальной скважины, где проницаемость может снизиться на 25% от первоначальной величины. с использованием критерия Кулона – Мора выявлены области разрушения горной породы от растяжения и сжатия. Отмечено, что с ростом депрессии исчезают области разрушения от растягивающих напряжений и увеличиваются области разрушения от сжатия. Анализ изменения коэффициента продуктивности в зависимости от депрессии показал, что при создании максимальной депрессии на пласт 12 МПа коэффициент продуктивности скважины может снизиться на 15% в связи с уплотнением породы-коллектора, вызванным увеличением эффективных напряжений.
Ключевые слова
Для цитирования:
Чернышов С.Е., Попов С.Н., Ван К., Дерендяев В.В., Ян Я., Хуацзе Л. Анализ изменения напряженно-деформированного состояния и проницаемости терригенного коллектора на основе численной модели околоскважинной зоны с элементами крепи и перфорационными каналами. Георесурсы. 2024;26(4):209-217. https://doi.org/10.18599/grs.2024.4.6
For citation:
Chernyshov S.E., Popov S.N., Wang X., Derendyaev V.V., Yang Y., Liu H. Analysis of Changes in the Stress-Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone With Casing and Perforation Channels. Georesursy = Georesources. 2024;26(4):209-217. (In Russ.) https://doi.org/10.18599/grs.2024.4.6
Введение
При разработке нефтегазовых месторождений, бурении, строительстве и заканчивании скважин часто применяются методы геомеханического моделирования (Zoback, 2007; Fjær et al., 2008; Кашников, Ашихмин, 2007). Широкое применение получили одномерные геомеханические модели, позволяющие оптимизировать траекторию ствола скважины при бурении и определить «окно плотности» бурового раствора для предотвращения аварийных ситуаций в процессе строительства скважин и гидроразрыва пород (Попов и др., 2023а; Лукин и др., 2016; Вашкевич и др., 2016; Попов, Чернышов, 2023), что особенно важно при бурении в сложных горно-геологических условиях. На основе одномерных моделей строятся трехмерные геомеханические модели, на базе которых можно получить поле распределения напряжений на всей территории месторождения, включая вышележащую толщу, и которые могут быть применены для анализа влияния изменяющихся эффективных напряжений в процессе снижения пластового давления на фильтрационно-емкостные свойства коллекторов и процесс разработки месторождений в целом (Wang et al., 2023; Попов, 2019; Кашников и др., 2019; Yang et al., 2017).
Геомеханическое моделирование активно применяется для прогноза эффективности создания трещин гидроразрыва в продуктивных пластах и определения геометрических характеристик таких трещин (Li et al., 2024; Liu et al., 2022; Safari et al., 2017), а также для предотвращения выноса песка из слабосцементированных коллекторов (Al-Awad, Al-Ahaidib, 2005; Araujo et al., 2014; Ермолаев и др., 2023). Для более детального анализа напряженного состояния вблизи скважины используются численные модели околоскважинных зон пласта (Чернышов и др., 2023; Чернышов и др., 2022; Fallahzadeh et al., 2010), учитывающие условия создания каналов методами кумулятивной, щелевой перфорации и др.
В настоящей работе рассмотрены особенности и результаты моделирования околоскважинной зоны на примере численной конечно-элементной модели, включающей обсадную колонну, цементный камень и нефтенасыщенные горные породы, а также учитывающей геометрию перфорационных каналов.
Разработка подобной модели позволит обеспечить достоверность расчетов при определении поля распределения напряжений в рассматриваемых элементах крепи скважин и горных породах, что, в свою очередь, позволит провести оценку устойчивости обсадной колонны, цементного камня и горных пород, а также изменения проницаемости горных пород в околоскважинной зоне и коэффициента продуктивности скважин.
Материалы и методы
Численный расчет напряжений вблизи скважины проводился с использованием программного комплекса конечно-элементного моделирования ANSYS, в котором заложены соотношения, описывающие поведение упругого и пороупругого материалов. Этот программный комплекс получил широкое применение при решении задач геомеханики в процессе разработки месторождений нефти и газа (Попов и др., 2023b; Zhang et al., 2022; Харламов и др., 2023).
Для расчета напряжений в обсадной колонне и цементом камне использовались соотношения, описывающие линейно-упругий материал:
– уравнения движения (моментов):
![]() ;
;
i, j = 1, 2, 3, (1)
где sji – компоненты тензора напряжений; ∂xj – производная по j-й координате; rfi – массовые силы;
– геометрические соотношения:
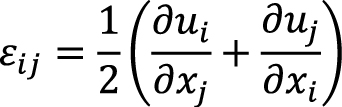 ;
;
i, j = 1, 2, 3, (2)
где eji – компоненты тензора деформаций; u – компоненты вектора перемещений;
– физические соотношения (в данном случае закон линейной упругости Гука):
![]()
где {s} – тензор напряжений; [D] – матрица упругих констант; {e} – тензор деформаций.
Для моделирования задач пороупругости в ANSYS заложена следующая система уравнений:
 (3)
(3)
где σ - тензор напряжений; σ' – тензор эффективных напряжений; a – коэффициент Био; p – поровое давление; I – единичный тензор второго порядка; f – вектор сил; εV– объемные деформации скелета породы; Km – модуль Био; q – вектор потока флюида; S – источник потока; • - оператор производной; ∇• -оператор дивергенции.
Для установления взаимосвязи напряжений и деформаций бралось соотношение:
![]() (4)
(4)
где εe – тензор деформаций; D – матрица упругих констант.
Поток флюида в пористой среде описывался с помощью закона Дарси:
![]() (5)
(5)
где k – тензор проницаемости второго порядка; ∇ – градиент-оператор; m – вязкость жидкости.
На рис. 1 представлена конечно-элементная схема, использованная при численном моделировании напряжено-деформированного состояния околоскважинной зоны. Модель разработана на основе типовых конструкций скважин, проектируемых на нефтяных месторождениях Пермского края. В табл. 1 представлены геометрические характеристики модели и упруго-прочностные свойства стальной обсадной колонны. Отметим, что кроме перфорационных каналов и продуктивных горных пород эта модель включает такие элементы конструкции скважины, как обсадная колонна и цементный камень. Для вычисления напряжений, давлений и скорости фильтрации флюида в породе-коллекторе использовались пороупругие трехмерные конечные элементы cpt215, а для имитации упругой среды стальной обсадной колонны и цементного камня – конечные элементы solid185.
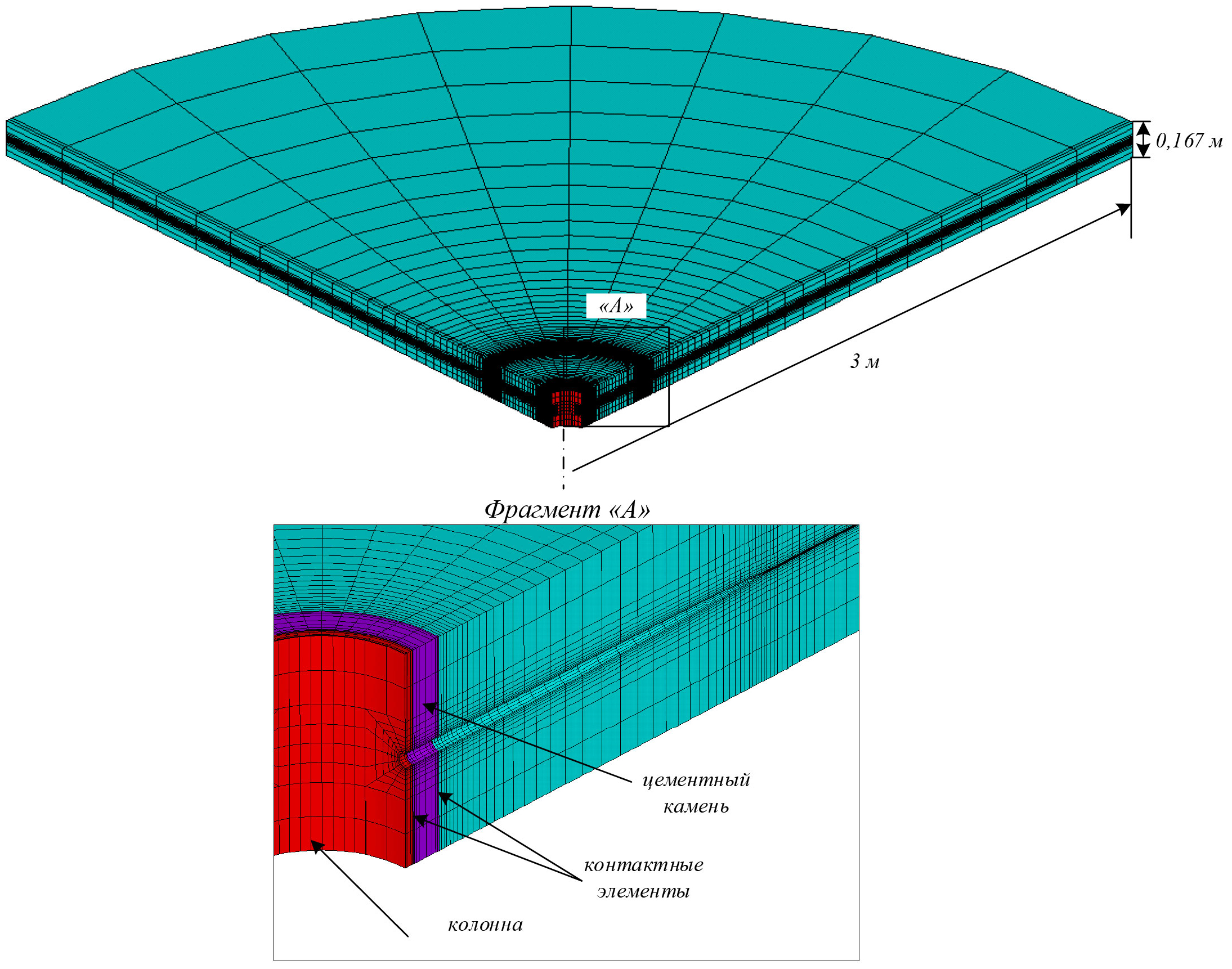
Рис. 1. Конечно-элементная схема, использованная для расчетов

Табл. 1. Геометрические характеристики модели и упруго-прочностные свойства обсадной колонны
Особенностью рассматриваемой конечно-элементной схемы является то, что на границах колонна – цемент и цемент – порода использовались контактные элементы, имитирующие скольжение цемента вдоль обсадной колонны и горных пород. Такой подход был использован в связи с тем, что если рассматривать модель со сплошными контактами, то при задании граничных условий в виде вертикальных напряжений на верхнюю границу конечно-элементной схемы за счет различных значений упругих характеристик обсадной колонны, цементного камня и горных пород возникают концентраторы напряжений на контактах указанных материалов, поэтому полученное распределение напряжений не будет соответствовать действительности. Для исключения данного эффекта в большинстве случаев исследователи в своих моделях задают на верхней границе модели граничное условие в виде перемещений, закрепленных по нормали к поверхности. Такой подход возможен, когда производится расчет напряжений вблизи открытого ствола вертикальной скважины или рассматривается скважина с крепью, но без перфорационных каналов. Однако если включить в модель перфорационные отверстия, то с такими граничными условиями будет некорректно рассчитываться вертикальная компонента напряжений.
В то же время если использовать контактные элементы и вызвать эффект проскальзывания материалов, такие концентрации напряжений будут отсутствовать, а радиальные напряжения от породы к цементному камню и колонне, а также в обратном направлении будут передаваться естественным образом.
С помощью такой модели можно более достоверно рассчитывать поле распределения напряжений (включая вертикальную компоненту) в околоскважинной зоне.
В связи с вышесказанным в расчетной модели задавались следующие граничные условия:
1) на нижней границе закреплялись вертикальные перемещения;
2) на левой и правой боковых границах конечно-элементной схемы (рис. 1) закреплялись перемещения по нормали к данным границам;
3) на внешней боковой поверхности устанавливались:
– давление флюида, которое вычислялось на основе давления на контуре питания и величины депрессии на пласт:
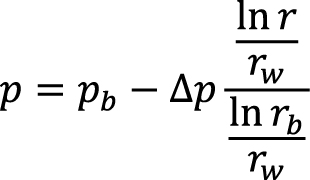 (6)
(6)
где p - определяемая величина давления, МПа; pb - давление на контуре питания, МПа; ∆p - депрессия на пласт, МПа; rb - радиус контура питания, м; rw - радиус скважины, м; r - радиус от центра скважины, для которого определяется величина давления, м;
– горизонтальное напряжение, рассчитанное по величинам вертикального напряжения и коэффициента Пуассона;
4) на верхней границе для колонны и цементного камня закреплялись перемещения по вертикали (имитация закрепленной скважины), для породы прикладывалось вертикальное напряжение, определенное на основе глубины залегания пласта и среднего объемного веса вышележащей толщи пород;
5) внутри скважины и на стенках перфорационных каналов задавалось давление флюида с учетом величины депрессии на пласт.
Для определения величины проницаемости породы в зависимости от средних эффективных напряжений в породе значение средних эффективных напряжений находилось в каждом конечном элементе модели по следующему соотношению:
![]() , (7)
, (7)
где σav - среднее эффективное напряжение, МПа; σ1, σ2, σ3 – главные эффективные напряжения, МПа.
Для оценки устойчивости горных пород и возникновения участков с пластическими деформациями использовался критерий Кулона – Мора в главных эффективных напряжениях:
![]() , (8)
, (8)
где σ1, σ3 - главные максимальные и минимальные напряжения, МПа; σc - предел прочности породы при одноосном сжатии, МПа; j - угол внутреннего трения, град; р - пластовое давление, МПа; α – коэффициент Био.
Упруго-прочностные свойства цементного камня установлены в нашем более раннем исследовании (Чернышов и др., 2023) и приведены в табл. 2.

Табл. 2. Упруго-прочностные характеристики цементного камня
Физико-механические свойства породы-коллектора и зависимость проницаемости от средних эффективных напряжений также определены нами ранее (Popov et al., 2023) и представлены в табл. 3 и на рис. 2. На рис. 2 приведено уравнение, по которому для каждого конечного элемента строилась зависимость относительной проницаемости от средних эффективных напряжений в каждом конечном элементе, и характерный пример такой зависимости.
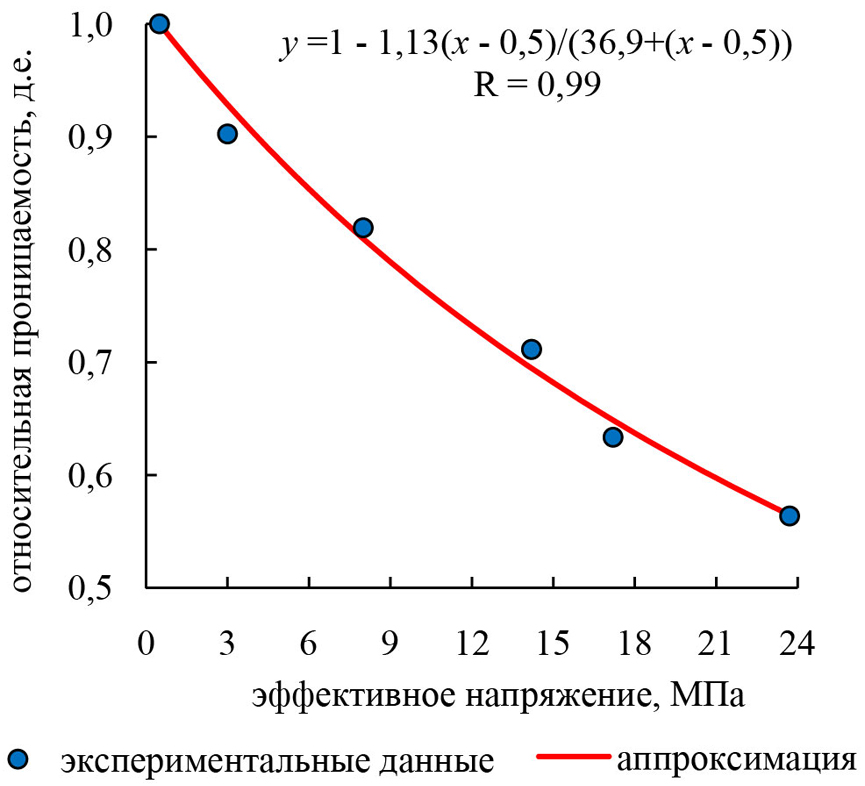
Рис. 2. Зависимость проницаемости от средних эффективных напряжений

Табл. 3. Характеристики продуктивного объекта, используемые в расчетах
На рис. 2 среднее эффективное напряжение, соответствующее начальным пластовым условиям, составляет 14,2 МПа.
Результаты
На рис. 3–7 представлены основные результаты, полученные при численном моделировании напряженно-деформированного состояния околоскважинной зоны.

Рис. 3. Коэффициент запаса прочности колонны при депрессии на пласт, равной: 0 (а), 3 (б), 6 (в) и 9 МПа (г)
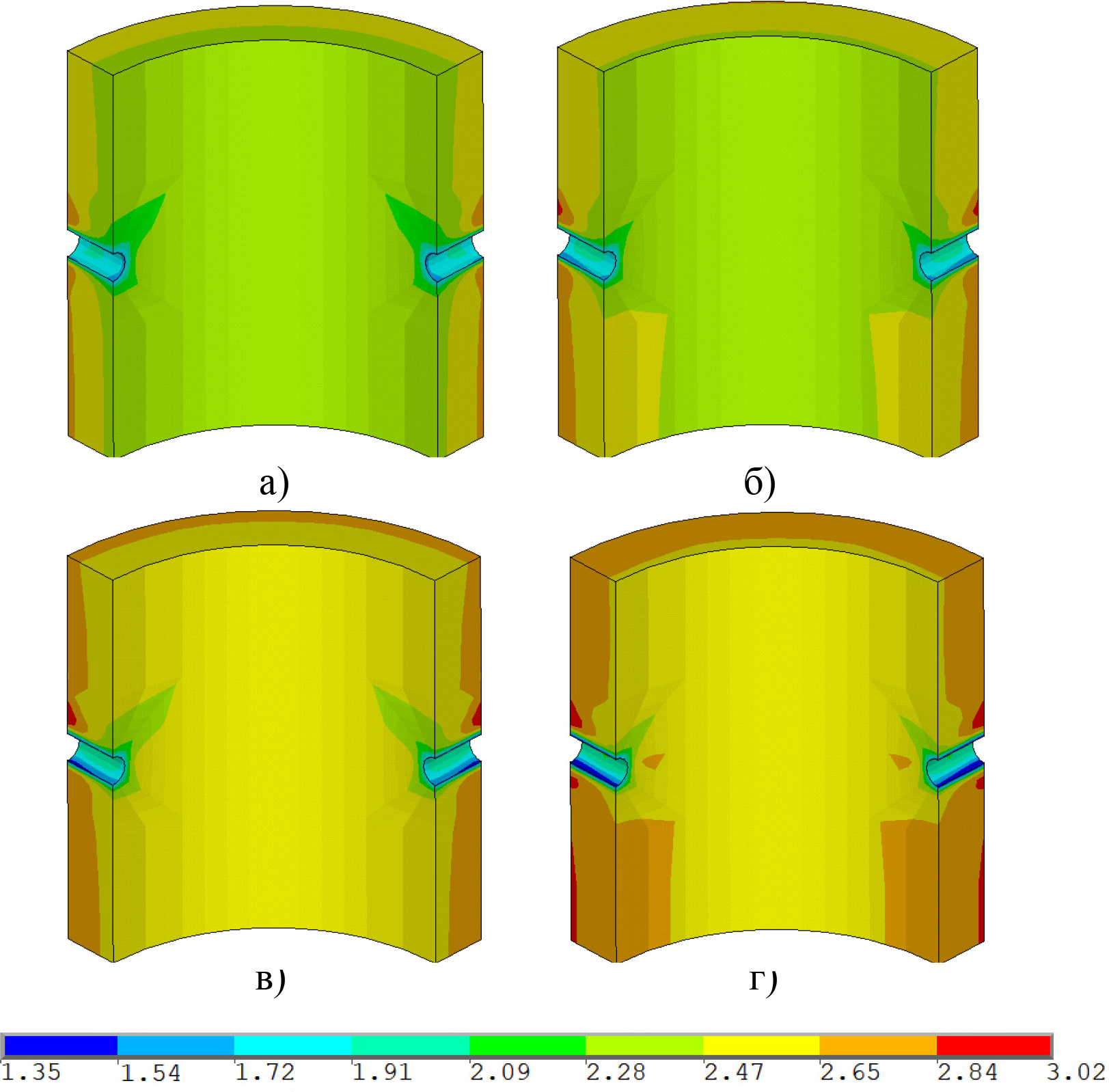
Рис. 4. Коэффициент запаса прочности цементного камня при депрессии на пласт, равной: 0 (а), 3 (б), 6 (в) и 9 МПа (г)
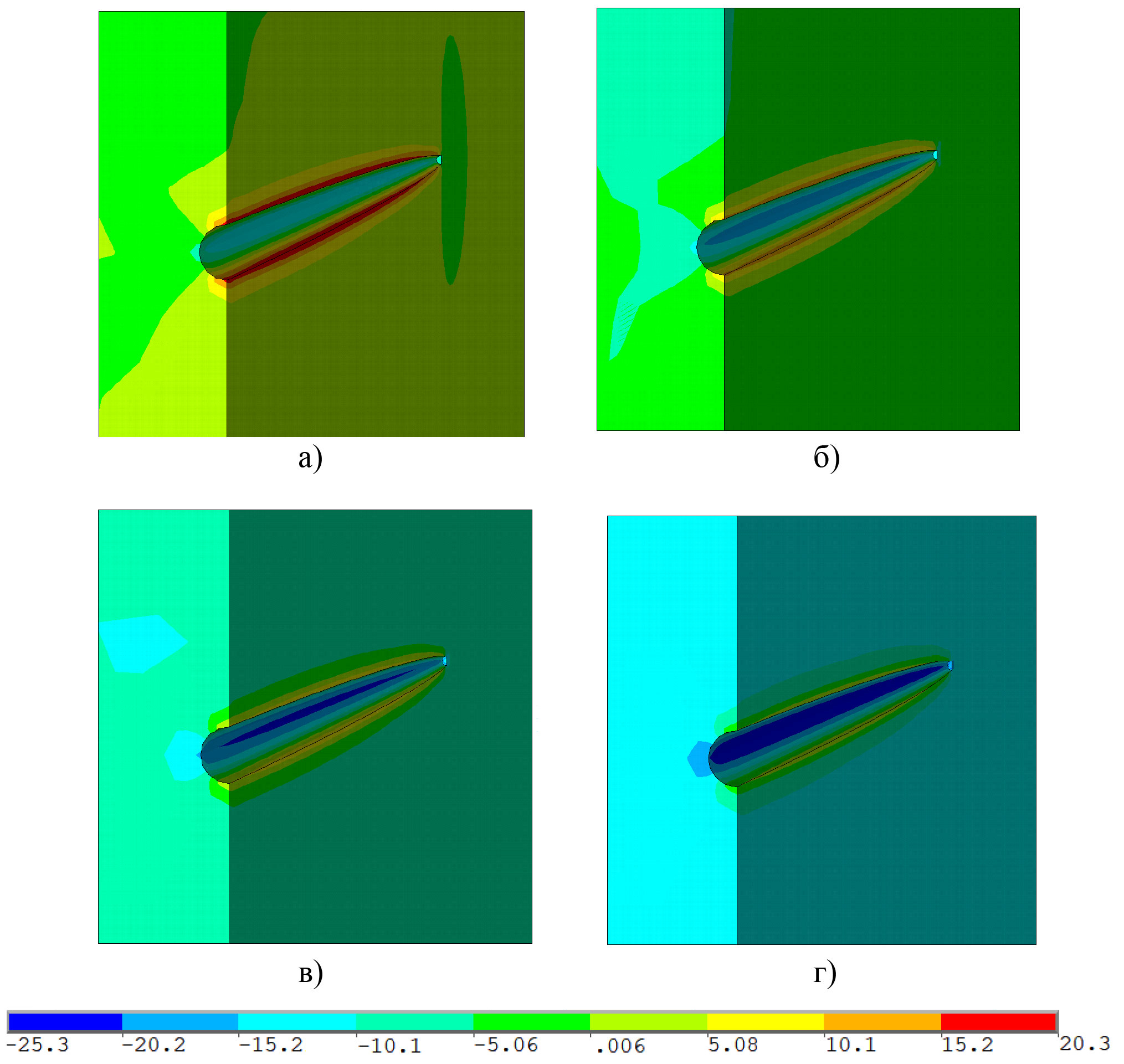
Рис. 5. Динамика изменения проницаемости породы (%) по соотношению к начальному значению при исходном пластовом давлении и депрессии на пласт, равной: 0 (а), 3 (б), 6 (в) и 9 МПа (г)
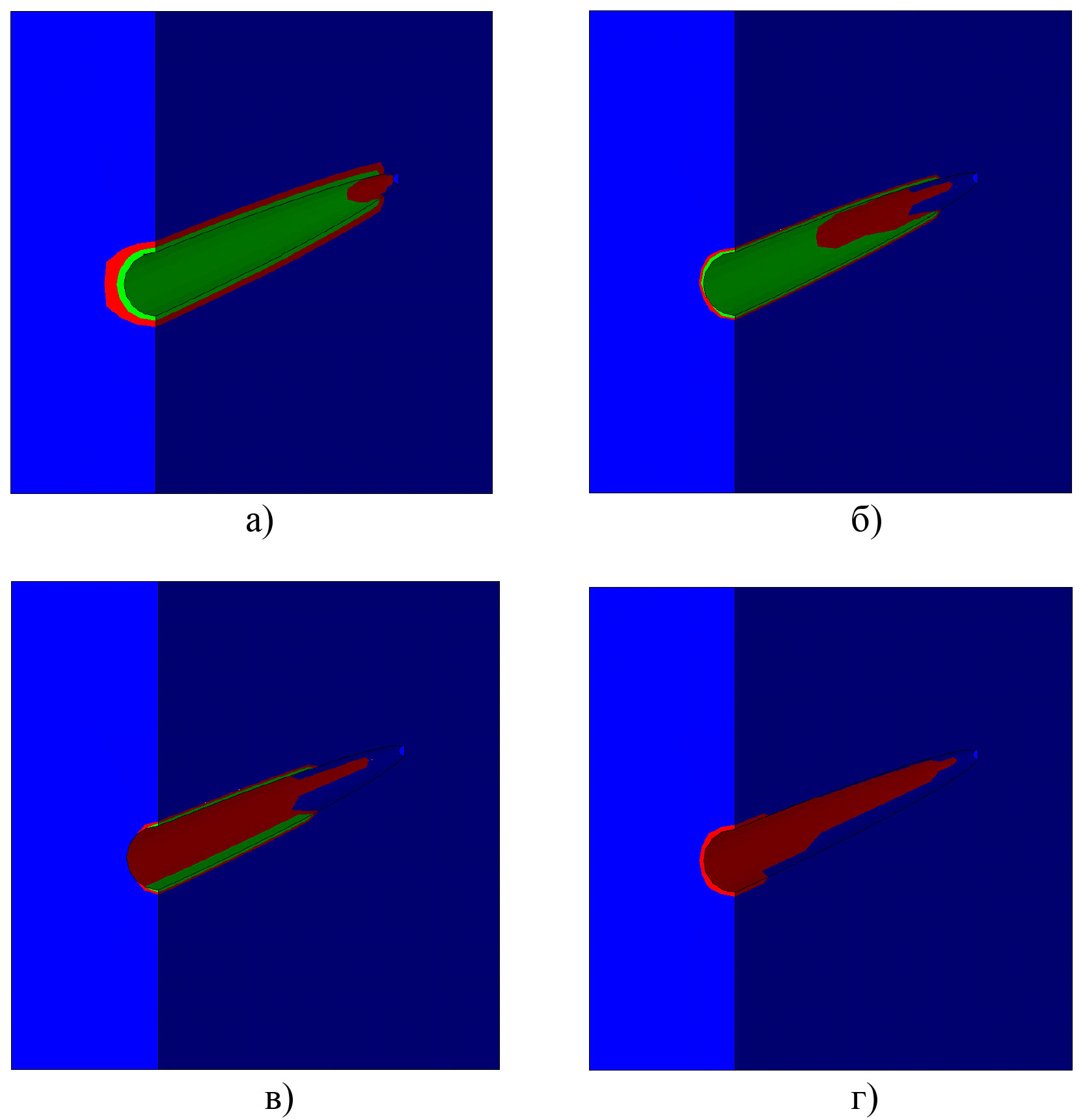
Рис. 6. Возможные зоны разрушения породы, определенные на основе критерия Кулона – Мора, при депрессии на пласт, равной: 0 (а), 3 (б), 6 (в) и 9 МПа (г). Зеленым цветом обозначены зоны разрушения от растягивающих напряжений, красным – от сжимающих

Рис. 7. Зависимость нормированного коэффициента продуктивности скважины от депрессии на пласт
Для стальной колонны и цементного камня напряжения анализировались с помощью коэффициента запаса прочности, который определялся из следующих соотношений:
– для обсадной колонны,
![]() , (9)
, (9)
где σY – предел текучести стали, МПа; σ1 – максимальное главное напряжение, Мпа;
– для цементного камня,
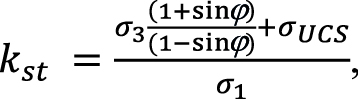 (10)
(10)
где σUCS – предел прочности цементного камня при одноосном сжатии, МПа; σ1 и σ3 – максимальное и минимальное главное напряжения соответственно, МПа.
Из рис. 3 следует, что колонна остается устойчивой вне зависимости от величины депрессии на пласт и запас прочности составляет 3–4 ед. Отметим также, что вблизи перфорационного канала возникают зоны как повышенных, так и пониженных напряжений. Участки с высокой нагрузкой расположены в верхней и нижней частях отверстия (рис. 3а), где коэффициент запаса прочности существенно снижается и близок к единице, что говорит о возможном возникновении нарушений целостности обсадной колонны на данных участках. При этом сами области достаточно небольшие и находятся на расстоянии, сопоставимом с радиусом отверстия.
На боковых участках отверстий, наоборот, возникают зоны разгрузки с низкими напряжениями, в которых коэффициент запаса прочности достигает 32 ед., однако эти зоны также достаточно небольшие.
Для цементного камня распределение коэффициента запаса прочности носит другой характер за счет сильно отличающихся упруго-прочностных свойств (рис. 4). Из рисунка видно, что в зависимости от депрессии на пласт коэффициент запаса прочности цементного камня варьирует примерно от 2 до 3 ед. и имеет наименьшее значение вблизи перфорационных каналов, оно составляет 1,35 ед. Наблюдается также рост разницы в значениях коэффициента запаса прочности цемента с увеличением депрессии на пласт: максимальный коэффициент запаса прочности растет, а минимальный – снижается.
Максимальное значение коэффициента запаса прочности зафиксировано на внешней стенке цементного камня, соприкасающейся с горными породами, а также на верхней и нижней стенках перфорационного канала.
На рис. 5 представлена динамика изменения проницаемости, вызванного трансформацией поля распределения напряжений в связи с созданием перфорационных каналов. Из рисунка видно, что даже при первоначальной величине давления (без депрессии на пласт) на боковой поверхности отверстия возникают области повышенных напряжений за счет воздействия вертикальной нагрузки от вышележащей толщи горных пород. В таких областях проницаемость сразу снижается примерно на 15% и при увеличении депрессии на пласт до 9 МПа снижение может достигать 25% от исходного значения.
В верхней и нижней частях перфорационных каналов, наоборот, происходит восстановление проницаемости за счет снижения величины напряжений. Так, при создании отверстий без депрессии на пласт проницаемость увеличивается на 20% от исходного значения. При росте депрессии область снижения напряжений уменьшается, при этом максимальная величина увеличения проницаемости достигает 10–15% на небольших участках.
На рис. 6 приведены возможные зоны разрушения горной породы вблизи перфорационного канала, при этом красным цветом обозначены участки разрушения от сжимающих напряжений, зеленым – от растягивающих. Как видно из рисунка, вдоль боковой поверхности канала возникает область разрушения от воздействия растягивающих напряжений, параллельно которой также находится область разрушения от сжатия. Следует подчеркнуть, что близость зон разрушения в результате растяжения и сжатия обусловлена тем, что при использовании критерия Кулона – Мора применялись эффективные напряжения, т.е. из полных напряжений вычиталась величина давления, умноженная на коэффициент Био (соотношение (8)).
В процессе увеличения депрессии на пласт области разрушения от растягивающих напряжений уменьшаются, что вызвано увеличением эффективных напряжений, и при депрессии, равной 9 МПа, такие зоны полностью исчезают и остаются только области разрушения от сжатия, которые, наоборот, увеличиваются при возрастании депрессии.
В работе также проведена оценка зависимости нормированного коэффициента продуктивности от депрессии на пласт (рис. 7). Несмотря на то что рассматривается участок скважины небольшой толщины, на основании предположения одинаковой проницаемости можно спрогнозировать изменение коэффициента продуктивности скважины, вызванное снижением проницаемости при увеличении депрессией на пласт.
Такой результат является следствием изменения проницаемости под воздействием эффективных напряжений, приведенного на рис. 5. Как видно из рис. 7, при создании максимальной депрессии 12 МПа снижение коэффициента продуктивности может достигнуть 15%, что говорит о необходимости поиска оптимального режима работы добывающей скважины.
Обсуждение и выводы
Проблема устойчивости конструктивных элементов скважины и коллектора, а также изменение проницаемости горных пород при вторичном вскрытии продуктивных пластов методом кумулятивной перфорации до сих пор остается актуальной и малоизученной. Во многих публикациях, посвященных этому направлению, либо рассматривается открытый ствол, либо не учитывается геометрия каналов перфорации. Вместе с тем при создании перфорационных отверстий происходит трансформация напряженного состояния горных пород-коллекторов за счет возникновения свободных от породы областей, а также при изменении забойного давления для создания депрессии на пласт. В настоящей работе разработана конечно-элементная модель, включающая перфорационные каналы, обсадную колонну, горную породу, цементный камень, и выполнено численное моделирование напряженно-деформированного состояния околоскважинной зоны добывающей скважины,
На базе полученных результатов можно сделать следующие основные выводы.
- Для исключения возникновения концентраций напряжений на границах сопредельных сред в модель включены контактные элементы на участках колонна – цемент и цемент – порода, в результате получено достоверное распределение напряжений в породе и конструктивных элементах скважины. Порода-коллектор моделировалась в виде пороупругой среды с проницаемостью, изменяющейся в зависимости от эффективных напряжений;
- Анализ распределения напряжений в обсадной колонне на основе коэффициента запаса прочности показал, что в основной части обсадной колонны значение данной характеристики составляет 3–4 ед., что говорит о ее высокой устойчивости. Исключение составляют небольшие участи вблизи перфорационных каналов, где данная величина близка к единице;
- Значение коэффициента запаса прочности для основной части цементного камня находится в диапазоне 2–3 ед., что также говорит о его достаточной прочности. Наименьший коэффициент запаса прочности цементного камня характерен для случая создания максимальной депрессии, а участки с его минимальным значением находятся вблизи перфорационных отверстий;
- Использование ранее определенной на образцах керна зависимости проницаемости от эффективных напряжений показало, что на поверхности перфорационных каналов возникают области повышенных (на боковых участках) и пониженных (в верхней и нижней части) напряжений. Вследствие чего в данных областях происходит как увеличение (до 20%), так и снижение (до 25%) проницаемости от исходных значений, вызванные разными эффективными напряжениями;
- При увеличении депрессии на пласт области увеличения проницаемости уменьшаются, а области со снижающейся проницаемостью увеличиваются, что вызвано увеличением эффективных напряжений;
- В результате анализа зон разрушения горных пород-коллекторов на основе критерия Кулона – Мора с учетом эффективных напряжений показано, что вблизи каналов образуются области разрушения как от сжимающих, так и от растягивающих напряжений. При увеличении депрессии на пласт области с растягивающими напряжениями уменьшаются, а затем совсем исчезают, а области с разрушением горных пород от сжимающей нагрузки увеличиваются, что также объясняется увеличением эффективных напряжений;
- Установлено, что за счет уменьшения проницаемости при увеличении депрессии на пласт до 12 МПа снижение коэффициента продуктивности скважины может достигнуть 15%, что обусловливает необходимость выбора оптимального режима работы добывающих скважин для предотвращения интенсивного уплотнения коллектора при увеличении эффективных напряжений вследствие снижения пластового давления.
Заключение
С применением численной конечно-элементной модели на основе коэффициента запаса прочности проведен анализ напряженного состояния обсадной колонны, цементного камня и участка горной породы вблизи скважины. Особенностью модели является использование контактных элементов и одновременное применение упругих (для обсадной колонны и цементного камня) и пороупругих (для горной породы) конечных элементов. Для оценки влияния деформационных эффектов на проницаемость коллектора использовалась полученная ранее зависимость изменения проницаемости от эффективных напряжений.
В результате численных расчетов установлено, что обсадная колонна и цементный камень обладают достаточным запасом прочности. Однако вероятно возникновение небольших зон разрушения вблизи каналов перфорации. Анализ изменений проницаемости позволил выявить области увеличения и уменьшения проницаемости горных пород, вызванные изменением напряжений в связи с образованием перфорационных отверстий, а также увеличением депрессии на пласт. При использовании критерия Кулона – Мора для анализа зон разрушения породы-коллектора установлено, что в зависимости от величины депрессии вблизи перфорационных каналов возникают области разрушения как от растягивающих, так и от сжимающих нагрузок. Показано также, что существенное увеличение депрессии на пласт может привести к снижению коэффициента продуктивности скважины до 15% от исходного значения.
Финансирование/Благодарности
Исследования выполнены при поддержке Министерства науки и высшего образования Российской Федерации (проект № FSNM-2023-0005).
Авторы выражают благодарность рецензентам и редакции за тщательное изучение работы и ценные комментарии, благодаря которым она была улучшена.
Список литературы
1. Вашкевич А.А., Жуков В.В., Овчаренко Ю.В., Бочков А.С. (2016). развитие подходов комплексного геомеханического моделирования в ПАО «Газпром нефть». Нефтяное хозяйство, (12), с. 16–19.
2. Ермолаев А.И., Ефимов С.И., Пятибратов П.В., Миниханов Е.Д., Дубиня Н.В., Леонова А.М. (2023). Оценка предельного забойного давления, исключающего разрушение призабойной зоны пласта, на основе геомеханических исследований керна. SOCAR Proceedings, (s1), с. 61–69. http://doi.org/10.5510/OGP2023SI100832
3. Кашников Ю. А., Ашихмин С.Г. (2007). Механика горных пород при разработке месторождений углеводородного сырья. М.: ооо «Недра Бизнес-центр», 476 с.
4. Кашников Ю.А., Ашихмин С.Г., Шустов Д.В., Якимов С.Ю., Кухтинский А.Э. (2019). Повышение эффективности разработки месторождений углеводородов на основе комплексных геомеханических исследований. Нефтяное хозяйство, (3), с. 66–69. http://doi.org/10.24887/0028-2448-2019-3-66-69
5. Лукин С.В., Есипов С.В., Жуков В.В., Овчаренко Ю.В., Хомутов А.Ю., Шевчук Т.Н., Сусляков И.В. (2016). Расчет устойчивости ствола скважины для предотвращения осложнений при бурении. Нефтяное хозяйство, (6), с. 70–73.
6. Попов С.Н. (2019). Разработка 3D геомеханической модели участка ачимовских отложений одного из месторождений Крайнего севера. Актуальные проблемы нефти и газа, (2), с. 1–17. http://doi.org/10.29222/ipng.2078-5712.2019-25.art3
7. Попов С.Н., Чернышов С.Е, Крив Ощеков С.Н. (2023а). Сопоставительный анализ аналитического и численного методов расчета напряженно-деформированного состояния околоскважинной зоны на основе упругой модели с учетом конструктивных элементов скважины. Известия Томского политехнического университета. Инжиниринг георесурсов, 334(5), с. 94–102. https://doi.org/10.18799/24131830/2023/5/3961
8. Попов С.Н., Чернышов С.Е. (2023). Разработка геомеханической модели и определение «окна плотности» бурового раствора в интервале фаменских продуктивных отложений (на примере участка одного из месторождений Тимано-Печорской нефтегазоносной провинции. Геология, геофизика и разработка нефтяных и газовых месторождений, (11), с. 32–39.
9. Попов А.Н., Исмаков Р.А., Попов М.А. (2023b). Прогнозирование гидроразрыва пористых горных пород в процессе бурения скважины. Строительство нефтяных и газовых скважин на суше и на море, (5), с. 20–24.
10. Харламов С.Н., Джанхорбани М., Зайковский В.В. (2023). транспорт шлама буровым раствором в горизонтальных скважинах. Часть 1. Моделирование структуры дисперсных частиц. Известия томского политехнического университета. Инжиниринг георесурсов, 334(10), с. 34–48. https://doi.org/10.18799/24131830/2023/10/4433
11. Чернышов С.Е., Попов С.Н., Варушкин С.В., Мелехин А.А., Кривощеков С.Н. Рен Ш. (2022). Научное обоснование методов вторичного вскрытия фаменских отложений юго-востока Пермского края на основании геомеханического моделирования. Записки Горного института, 527, с. 732–743. https://doi.org/10.31897/PMI.2022.51
12. Чернышов С.Е., Попов С.Н., Савич А.Д., Дерендяев В.В. (2023). Анализ устойчивости крепи нефтедобывающих скважин при проведении кумулятивной перфорации на основе результатов геомеханического моделирования. Георесурсы, 25(2), с. 245–253. https://doi.org/10.18599/grs.2023.2.18
13. Al-Awad M.N.J., Al-Ahaidib T.Y. (2005). Estimating the amount of free sand in the yielded zone around horizontal oil wells. SPE Technical Symposium of Saudi Arabia Section, SPE-106329-MS. https://doi.org/10.2118/106329-MS
14. Araujo E.F., Alzate-Espinosa G.A., Arbeláez-Londoño A., Peña Clavijo S., Cardona Ramirez A., Naranjo Agudelo A. (2014). Analytical prediction model of sand production integrating geomechanics for open hole and cased – perforated wells. SPE Heavy and Extra Heavy Oil Conference, SPE-171107MS. https://doi.org/10.2118/171107-MS
15. Fallahzadeh S.H., Shasizadeh S.R., Pourafshary P., Zare M.R. (2010). Modeling the Perforation Stress Profile for Analyzing Hydraulic Fracture Initiation in a Cased Hole. Nigeria Annual International Conference and Exhibition, SPE-136990-MS. https://doi.org/10.2118/136990-MS
16. Fjær E., Holt R.M., Horsrud P., Raaen A.M., Risnes R. (Eds.) (2008). Petroleum related rock mechanics. Amsterdam: Elsevier, 492 p.
17. Li W., Chen L., Wang X., Fan Q., Xu G., Xiao W., Li X., Ye Zh. (2024). Acid fracturing technology and effect evaluation of carbonate horizontal well in Fuman oilfield. Journal of Physics: Conference Series, 2679, 012010. https://doi.org/10.1088/1742-6596/2679/1/012010
18. Liu F., Fan Y., Li L., Li J., Chen Y., Lv Z., He T. (2022). Case study of successfully staged acid fracturing on the ultra-deep horizontal well for the Qixia fm HTHP tight carbonate gas reservoir in China. Frontiers in Energy Research, 10, 917740. https://doi.org/10.3389/fenrg.2022.917740
19. Popov S., Chernyshov S., Gladkikh E. (2023). Experimental and numerical assessment of the influence of the bottommhole pressure drawdown on terrigenous reservoir permeability and well productivity. Fluid Dynamics & Materials Processing, 19(3), pp. 619–634. https://doi.org/10.32604/fdmp.2022.021936
20. Safari R., Smith C., Fragachan F. (2017). Improved recovery of carbonate reservoir by optimizing acidizing strategy: coupled wellbore, reservoir, and geomechanical analysis. Abu Dhabi International Petroleum Exhibition & Conference, SPE-188683-MS. https://doi.org/10.2118/188683-MS
21. Wang L. Shen X., Wu B., Shen T., Shi J. (2023). Integrated analysis of the 3D geostress and 1D geomechanics of an exploration well in a new gas field. Energies, 16(2), 806. https://doi.org/10.3390/en16020806
22. Yang Y., Liu Z., Sun Z., An S., Zhang W., Liu P., Yao J., Ma J. (2017). Research on stress sensitivity of fractured carbonate reservoirs based on CT technology. Energies, 10(11), 1833. https://doi.org/10.3390/en10111833
23. Zhang J., Moridis G., Blasingame Th.A. (2022). Message passing interface (MPI) parallelization of iteratively coupled fluid flow and geomechanics codes for the simulation of system behavior in hydrate-bearing geological media. Part 1: methodology and validation. SPE Reservoir Evaluation & Engineering, 25(03), pp. 600–620. https://doi.org/10.2118/206161-PA
24. Zoback M.D. (2007). Reservoir Geomechanics. Cambridge, U.K.: Cambridge University Press, 505 p.
Об авторах
С. Е. ЧернышовРоссия
Сергей Евгеньевич Чернышов – доктор техн. наук, доцент, заведующий кафедрой Нефтегазовые технологии.
614990, Пермь, Комсомольский проспект, д. 29
С. Н. Попов
Россия
Сергей Николаевич Попов – доктор техн. наук, заведующий лабораторией, главный научный сотрудник лаборатории нефтегазовой механики и физикохимии пласта.
119333, Москва, ул. Губкина, д. 3
К. Ван
Китай
Ксяопу Ван – PhD, доцент, Школа нефтяного инжиниринга.
266580, провинция Шаньдун, Циндао, ЧанцзянВест-роуд, 66
В. В. Дерендяев
Россия
Вадим Валерьевич Дерендяев – ассистент, младший научный сотрудник кафедры Нефтегазовые технологии.
614990, Пермь, Комсомольский проспект, д. 29
Я. Ян
Китай
Янфей Ян – профессор, доктоРАНт, Школа нефтяного инжиниринга.
266580, провинция Шаньдун, Циндао, Чанцзян-Вест-роуд, 66
Л. Хуацзе
Китай
Хуацзе Лю – PhD, доцент, Школа нефтяного инжиниринга.
266580, провинция Шаньдун, Циндао, ЧанцзянВест-роуд, 66
Рецензия
Для цитирования:
Чернышов С.Е., Попов С.Н., Ван К., Дерендяев В.В., Ян Я., Хуацзе Л. Анализ изменения напряженно-деформированного состояния и проницаемости терригенного коллектора на основе численной модели околоскважинной зоны с элементами крепи и перфорационными каналами. Георесурсы. 2024;26(4):209-217. https://doi.org/10.18599/grs.2024.4.6
For citation:
Chernyshov S.E., Popov S.N., Wang X., Derendyaev V.V., Yang Y., Liu H. Analysis of Changes in the Stress-Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone With Casing and Perforation Channels. Georesursy = Georesources. 2024;26(4):209-217. (In Russ.) https://doi.org/10.18599/grs.2024.4.6














.png)


