Перейти к:
Особенности применения моделей неравновесного фазового поведения в задачах разработки месторождений углеводородов: критический обзор
https://doi.org/10.18599/grs.2025.3.17
Аннотация
Для корректного моделирования фазового поведения флюида и точного учета компонентного состава, долей и свойств присутствующих в пласте фаз при разработке месторождений углеводородов в некоторых случаях необходимо использовать модели неравновесного фазового поведения.
Наблюдаемые при разработке месторождений признаки неравновесного фазового поведения флюидов могут быть связаны с различными факторами. Экспериментально показано, что так называемая термодинамическая неравновесность (когда фазовый переход нельзя считать мгновенным по сравнению с характерным темпом изменения параметров состояния системы) проявляется при ограниченной удельной площади поверхности раздела фаз. «Гидродинамическая неравновесность» (отличие фактической пропорции добываемых фаз от ожидаемой) может возникать при высоких скоростях отбора по той причине, что одна из фаз не успевает сегрегировать и переносится в виде взвеси во второй фазе, без формирования отдельной сплошной среды. Правильная идентификация типа наблюдаемой неравновесности является ключевым фактором при выборе корректной модели.
В статье рассмотрены особенности различных моделей учета неравновесного фазового поведения. Проанализированы примеры их практического применения при различных проявлениях неравновесного фазового поведения и причинах его возникновения. Обсуждается проблема моделирования фильтрации, сопровождающейся неравновесными фазовыми переходами.
Ключевые слова
Для цитирования:
Лобанова О.А., Индрупский И.М. Особенности применения моделей неравновесного фазового поведения в задачах разработки месторождений углеводородов: критический обзор. Георесурсы. 2025;27(3):252-266. https://doi.org/10.18599/grs.2025.3.17
For citation:
Lobanova O.A., Indrupskiy I.M. Application specifics of nonequilibrium phase behavior models in the development of hydrocarbon deposits: a critical review. Georesursy = Georesources. 2025;27(3):252-266. (In Russ.) https://doi.org/10.18599/grs.2025.3.17
Введение
Разработка месторождений нефти и газа сопровождается отбором и закачкой различных углеводородных и неуглеводородных флюидов. Это, в свою очередь, нередко приводит к возникновению интенсивного массообмена между находящимися в пласте жидкой и газовой фазами.
Одним из примеров подобных процессов может служить добыча трудноизвлекаемых углеводородов. Методы повышения нефте- и конденсатоотдачи, применяемые на месторождениях с трудноизвлекаемыми запасами, включают закачку углекислого газа, растворителей, полимерных растворов, воздействие углеводородным газом и др.
Методы разработки, основанные на использовании внутрипластовой энергии, сопровождаются разгазированием в нефтяных залежах и выпадением конденсата из газоконденсатных пластовых смесей. В результате этого также возникает обмен компонентами между жидкой и газовой углеводородными фазами.
Необходимость выбора наиболее эффективного метода разработки месторождения требует использования моделей, позволяющих выполнять корректное описание фазового поведения флюида и более точный учет компонентного состава, долей и свойств присутствующих в пласте фаз. Нередко возникает необходимость прибегать к моделям неравновесного фазового поведения, когда характерное время фазовых переходов становится сопоставимым с характерными временами изменения гидродинамических параметров в элементарном объеме пласта. В качестве примеров можно привести разработку нефтяных месторождений после разгазирования, сопровождающуюся обратным растворением газа при повышении пластового давления; поздние стадии разработки газоконденсатных месторождений на естественном режиме при давлениях ниже давления максимальной конденсации; сайклинг-процесс; газовые методы повышения нефтеотдачи (Бриллиант и др., 2014; Лобанова и др., 2016).
Несмотря на то, что вопрос моделирования неравновесного фазового поведения рассматривается достаточно длительное время, предложено всего несколько основных моделей для его учета. Это связано, во-первых, с недостатком экспериментальных данных о зависимостях коэффициентов неравновесной модели от различных параметров пористой среды и состава насыщающих ее углеводородных флюидов по причине сложности постановки таких исследований и необходимости учета при этом большого числа переменных факторов.
С другой стороны, наблюдаемые при разработке месторождений признаки неравновесного фазового поведения углеводородов могут быть связаны с различными факторами. Экспериментально показано, что так называемая термодинамическая неравновесность (т.е. не мгновенный фазовый переход) проявляется при ограниченной удельной площади границы раздела фаз (Gorodetskii et al., 2005; Лобанова и др., 2014). «Гидродинамическая неравновесность» (т.е. отличие фактической пропорции добываемых фаз от ожидаемой) наблюдается при высоких скоростях отбора по той причине, что одна из фаз не успевает сегрегироваться и присутствует в виде взвеси во второй фазе, без формирования отдельной сплошной среды (Dorhjie et al., 2024). Вместе с тем причина наблюдаемой неравновесности фазового поведения является ключевым фактором при выборе необходимой модели его учета.
В настоящей работе на основе актуального анализа публикаций рассмотрены существующие модели учета неравновесного фазового поведения, а также возможность их практического использования в коммерческих гидродинамических симуляторах. Критически оценивается применимость моделей неравновесного поведения при различных определяющих его факторах. Приведены примеры использования неравновесных моделей при проектировании разработки реальных месторождений углеводородов. Обсуждается возможность учета фазового поведения на основе релаксационной модели при фильтрации неравновесных фаз.
В рамках данной статьи рассматриваются, в основном, изотермические модели. Но обсуждаемые принципы и особенности переносимы и на случай неизотермических процессов. Также для упрощения записи уравнений вода считается инертной фазой и исключается из рассмотрения, а насыщенности жидкой и газовой (паровой) фаз нормируются по углеводородонасыщенному (эффективному) объему пор.
Традиционная модель многокомпонентной фильтрации с неравновесными фазовыми превращениями
Модель изотермической многокомпонентной фильтрации с учетом неравновесных фазовых превращений, предполагающая удвоение числа используемых уравнений неразрывности, является наиболее теоретически обоснованной и разработанной (Розенберг, Кундин, 1976; Максимов, 1994; Nghiem, Sammon, 1997).
В модели уравнения неразрывности для учета баланса массы (числа молей) каждого компонента смеси записывают отдельно для всех сосуществующих углеводородных фаз. При этом в них вводится дополнительное слагаемое ωi,L-V , характеризующее интенсивность обмена данным компонентом между фазами:
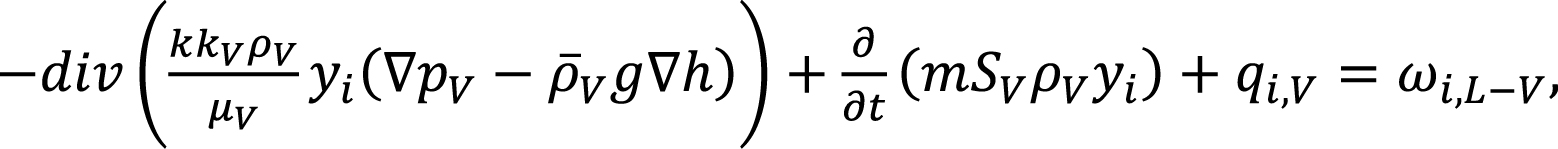 (1)
(1)
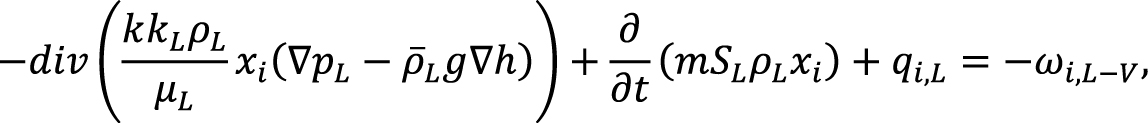 (2)
(2)
где N – число компонентов смеси; i=1,…,N – номер компонента; индексы V, L обозначают паровую и жидкую углеводородные фазы; kV, kL – относительные фазовые проницаемости; μ – динамическая вязкость; ρ – мольная плотность; 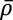 – массовая плотность; m – эффективная пористость; k – эффективная проницаемость (фазовая проницаемость для нефти при остаточной водонасыщенности); S – насыщенность, нормированная по эффективному поровому объему; yi, xi – мольная доля компонента i в паровой и жидкой фазах соответственно; qi – мольная интенсивность источников (стоков) компонента i; h – глубинная отметка данной точки, g – ускорение свободного падения, ωi,L-V – интенсивность межфазного потока i-го компонента (из жидкой фазы в паровую).
– массовая плотность; m – эффективная пористость; k – эффективная проницаемость (фазовая проницаемость для нефти при остаточной водонасыщенности); S – насыщенность, нормированная по эффективному поровому объему; yi, xi – мольная доля компонента i в паровой и жидкой фазах соответственно; qi – мольная интенсивность источников (стоков) компонента i; h – глубинная отметка данной точки, g – ускорение свободного падения, ωi,L-V – интенсивность межфазного потока i-го компонента (из жидкой фазы в паровую).
В большинстве случаев в качестве замыкающих соотношений для системы (1)–(2) из термодинамических соображений выбирают зависимость потока i-го компонента ωi,L-V вида (Розенберг, Кундин, 1997):
![]() , (3)
, (3)
где µi,V = RTlnfi,V + µi0, µi,L = RTlnfi,L + µi0 – химические потенциалы i-го компонента фазе, R – универсальная газовая постоянная, µi0 – химический потенциал i-го компонента смеси в идеально газовом состоянии при температуре T и единичном давлении. Причем коэффициент С зависит как от свойств пласта (например, пористости), так и от гидродинамических переменных (например, насыщенностей). Расчет химических потенциалов может выполняться стандартными способами равновесной термодинамики (Брусиловский, 2002).
Кроме соотношений (3) для замыкания системы (1)–(2) задаются зависимости свойств пласта и флюидов от давлений, насыщенностей и составов фаз (долей компонентов в фазах), а также начальные и граничные условия в зависимости от постановки конкретной задачи.
Отметим, что в отличие от равновесной постановки, граничные условия на компонентные составы фаз для (1)–(3) могут быть неравновесными по отношению к составам фаз в примыкающих к границам ячейках. Зачастую граничные условия заменяются дополнительными источниками/стоками.
Основным недостатком подобных моделей является отсутствие экспериментальных данных о значениях коэффициентов межфазного переноса вещества, необходимых для практического применения модели и прогнозирования составов и долей неравновесных углеводородных фаз. Как говорилось выше, трудность их экспериментального получения состоит в том, что они зависят от давления, долей и составов фаз и характеристик пористой среды. Таким образом, необходимо проводить многократные эксперименты по многокомпонентной фильтрации с контролем изменения составов углеводородных фаз и интерпретировать их результаты с применением моделей неравновесной фильтрации. Кроме того, соответствующие зависимости различны на разных масштабах моделирования, что не позволяет осуществить непосредственный перенос полученных экспериментальных данных в модели разработки реального пласта.
В работе (Nghiem, Sammon, 1997) вместо (3) предложена зависимость межфазного потока компонентов от разности текущей и равновесной концентрации компонента в каждой фазе с учетом коэффициентов диффузии и геометрических характеристик элементарного объема моделирования пористой среды, предопределяющих среднее расположение флюидов в порах относительно межфазной границы:
![]() , (4)
, (4)
где [A/L] – отношение характерной площади межфазной границы в сеточной ячейке численной модели к характерному расстоянию до межфазной границы (геометрическая характеристика элементарного объема моделирования), Sk – насыщенность фазы k, ρk – мольная плотность фазы k, Dik – коэффициент диффузии компонента i в фазе k, F – коэффициент удельного сопротивления пласта (влияние пористой среды на диффузию), yik – мольная доля компонента i в фазе k, yik* – равновесная доля компонента i в фазе k на границе, рассчитанная в каждом блоке сетки. Конкретный вид зависимости для [A/L] авторы (Nghiem, Sammon, 1997) предлагают выбирать, исходя из направления вытеснения.
Недостатком такого способа задания межфазного потока компонентов является необходимость вспомогательного расчета равновесных концентраций компонентов в фазах. Также неясное обоснование имеют отождествление геометрических параметров для диффузионного процесса с размерами сеточной ячейки и возможность учета влияния пористой среды через величину F. Неочевидно, какие экспериментальные процедуры требуются для достоверного её определения с учетом неоднородности пласта и влияния масштабного эффекта при переходе от керна к масштабу залежи при моделировании фильтрации.
Для того чтобы яснее представить взаимосвязь коэффициентов межфазного переноса с различными факторами, можно обратиться к работе (Булейко, Вовчук, 2010). В данной публикации приведена зависимость потоков (Ji) от вызывающих их сил (Fk) в рамках линейной неравновесной термодинамики:
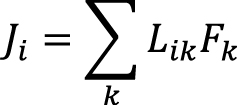 . (5)
. (5)
Величины Lik называются феноменологическими коэффициентами и зависят, в общем случае, от переменных состояния.
Диагональные члены в (5) характеризуют прямой эффект, соответствующий основной действующей силе. А именно, J1 – макроскопический поток массы (основная сила – градиент давления gradP), J2 – диффузионный поток (основная сила – градиент химического потенциала gradµn или градиент концентрации gradcn), J3 – сорбционно-десорбционный поток (основная сила – градиент сорбционно-десорбционного потенциала gradφсорб.), J4 – тепловой поток (основная сила – градиент температуры gradT), J5 – электрический поток (основная сила – градиент электрического потенциала gradUэл.).
Перекрестные члены (5) описывают влияние налагающих явлений для соответствующего потока.
Вклад каждого слагаемого LikFk в поток Ji зависит от свойств системы. Например, для высокопроницаемого песчаного коллектора, насыщенного газом, в макроскопическом потоке массы будет превалировать первое слагаемое L11F1, т.е. выполняться закон Дарси. В плотном низкопроницаемом коллекторе с большой удельной поверхностью вклад других слагаемых будет расти. В частности, вклад сорбции-десорбции (L13F3) увеличивается, вплоть до превышения вклада L11F1.
Таким образом, в сложных коллекторах не удается выделить одну определяющую силу, контролирующую поток компонентов углеводородной смеси. При проведении экспериментальных исследований по определению коэффициентов массопереноса, необходимых для практического использования системы (1)–(2), должны быть выявлены и учтены все слагаемые LikFk, вносящие существенный вклад в поток Ji, что значительно усложняет постановку и увеличивает количество соответствующих экспериментов.
В работе (Курбанов и др., 1966) авторы столкнулись с указанной проблемой отсутствия экспериментальных данных о значениях коэффициентов межфазного массопереноса. При моделировании двухфазной фильтрации многокомпонентного углеводородного флюида они вынуждены были принять условные значения коэффициентов массопереноса, ограничившись рассмотрением двухкомпонентной смеси метан-декан и оценкой предельного отклонения характеристик неравновесного процесса от соответствующих равновесных значений. Погрешность применения такого подхода для реальной многокомпонентной смеси не оценивалась.
Для определения скорости межфазного массопереноса авторами (Mohamadi-Baghmolaei et al., 2019) рассмотрено использование числа Шервуда Sh, выполнен ряд экспериментов и проведено моделирование закачки газа в истощенную газоконденсатную систему для извлечения выпавшего конденсата. Число Шервуда представляет собой отношение общей скорости массопереноса (конвективной и диффузионной составляющих) к скорости диффузионного массопереноса. В качестве закачиваемых газов использовались СО2, N2 и CH4, в качестве конденсата – C5H12, C6H14 и C7H16. Средний размер зерен трех образцов керна составлял 150–300 мкм. Авторами предложены корреляционные зависимости числа Шервуда от скорости закачки и среднего размера зерен породы:
![]() , (6)
, (6)
где Pe – число Пекле (отношение между скоростями конвективного и диффузионного переноса массы), Sc – число Шмидта (отношение коэффициента кинематической вязкости к коэффициенту диффузии), U – нормализованная скорость, dn – средний размер зерен (в мкм).
Предложенная корреляция показала хорошее совпадение с фактическими данными для условий, соответствующих выполненным экспериментам. Однако, результаты указанной выше работы (Булейко, Вовчук, 2010) демонстрируют, что силы, приводящие к неравновесному потоку массы, в различных типах коллекторов и флюидальных систем могут иметь принципиально различную природу. Поэтому использовать данную корреляцию при других промысловых и экспериментальных условиях не представляется возможным.
Надо отметить, что корреляционные зависимости числа Шервуда при различных типах закачиваемого флюида предлагались исследователями-экспериментаторами и ранее. Соответствующие формулы и ссылки на первоисточники также приведены в (Mohamadi-Baghmolaei et al., 2019). К сожалению, они также не носят универсального характера и могут использоваться только для условий, характерных для конкретных экспериментов.
Авторы (Григорьев, Сокотущенко, 2019) также отмечают, что коэффициенты межфазного массопереноса для реальных нефтегазовых и газоконденсатных месторождений зависят от характеристик пористой среды, давления, насыщенности и составов фаз. А для их определения необходимо проводить специальные сложные лабораторные эксперименты.
В отсутствие таких экспериментов авторы предлагают аналитическую формулу для вычисления среднего по компонентам коэффициента межфазного переноса λ:
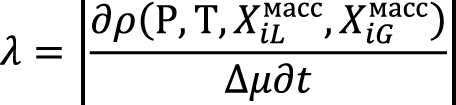 , (7)
, (7)
где для определения плотности смеси ρ и химических потенциалов µ используют аналитические соотношения, указывая при этом, что плотность и химические потенциалы зависят от давления Р, температуры Т и составов фаз XiGмасс, XiLмасс и должны определяться экспериментально. Очевидно, что данный подход для реального месторождения позволяет получить лишь приближенную оценку значений коэффициентов массопереноса.
Остается также открытым вопрос, каким образом выполнять ремасштабирование полученных в ходе эксперимента значений коэффициентов межфазного массопереноса при переходе на масштаб залежи.
Таким образом, можно заключить, что использование традиционной неравновесной модели для практической реализации в современных гидродинамических симуляторах не представляется целесообразным. Во-первых, из-за сложности постановки экспериментов по определению коэффициентов межфазного массопереноса. Во-вторых, из-за необходимости существенного изменения программного кода ядра гидродинамического симулятора и размерности систем уравнений по сравнению с общепринятой реализацией модели равновесной многокомпонентной фильтрации – в связи с переходом от записи уравнения неразрывности для компонента в сумме по фазам к записи отдельного уравнения для компонента в каждой фазе.
Релаксационная модель неравновесных фазовых превращений
Для эффективной практической реализации была предложена принципиально иная модель учета неравновесного фазового поведения (Лобанова, Индрупский, 2012; Indrupskiy et al., 2017).
Как отмечалось выше, роль обобщенной силы при диффузии играет градиент химического потенциала. Диффузионный поток компонента направлен из области с большим значением химического потенциала в область с его меньшим значением. Поэтому разность химических потенциалов компонента в фазах определяет направление массообмена между ними. Условием термодинамического равновесия многокомпонентной системы является равенство химических потенциалов (летучестей) компонентов в фазах (Брусиловский, 2002).
При моделировании многокомпонентной фильтрации для расчета равновесных составов и долей фаз смеси в каждом элементарном объеме необходимо решать систему уравнений, включающую условия равновесия и условия нормировки концентраций (Брусиловский, 2002; Whitson, Brule, 2000):
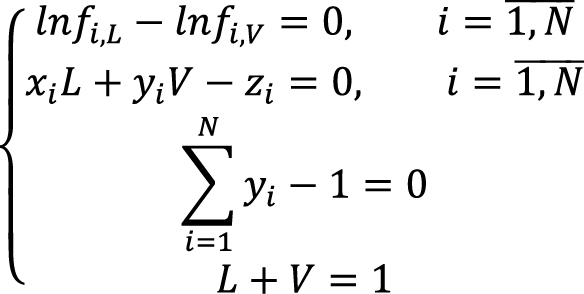 (8)
(8)
где V, L – мольные доли паровой и жидкой фаз, на которые разделяется исходная смесь; fi,L и fi,V – летучесть компонента i в жидкой и паровой фазах соответственно, zi – заданный текущий суммарный состав (мольная доля компонента i) углеводородной смеси, причем сумма zi равна единице.
Если в результате какого-либо внешнего воздействия система выведена из состояния равновесия, в ней начинают происходить процессы, направленные на достижение нового состояния равновесия. Этот процесс протекает с некоторым характерным временем. Если оно значительно по сравнению с характерным временем изменения внешних условий и им не удается пренебречь, то процесс стремления к равновесию может быть описан как релаксационный. Исходя из (3), для нахождения составов и долей фаз вместо равновесной системы (8) необходимо решить неравновесную систему:
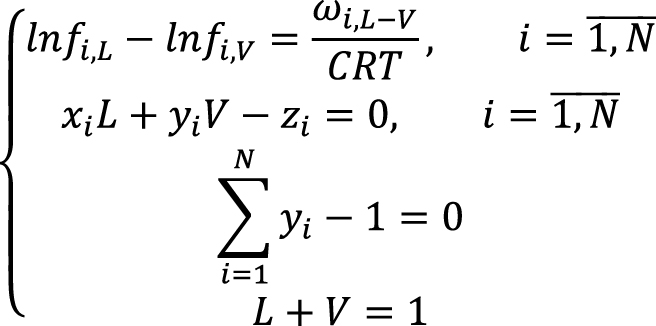 (9)
(9)
В (Indrupskiy et al., 2017) было предложено правую часть в первом уравнении системы (9)
![]()
выразить через решение уравнения релаксации для разности химических потенциалов на одном шаге по времени:
![]() (10)
(10)
где λ – параметр, обратный к характерному времени релаксации и уточняемый при настройке модели; Δt – величина шага по времени; а индекс j характеризует номер временного слоя, причем все величины в расчете левой части уравнений (9) принимаются на новом слое j. Таким образом, выражение (10) после подстановки в (9) соответствует релаксации составов фаз и связанной с ними разности химических потенциалов в направлении равновесного состояния в течение времени Δt после изменения давления со значения p j-1на p j.
Выражения (9)–(10) отражают пропорциональную зависимость между нормированной интенсивностью межфазного потока компонента и нормированной разностью химических потенциалов компонента в двух фазах. Нормированная интенсивность потока компонента ![]() убывает от начального значения к нулю по мере релаксации составов фаз к равновесным. Таким образом, степень отклонения текущего фазового состояния от равновесного зависит от λ (скорости релаксации) и темпа изменения давления (скорости изменения равновесного состояния).
убывает от начального значения к нулю по мере релаксации составов фаз к равновесным. Таким образом, степень отклонения текущего фазового состояния от равновесного зависит от λ (скорости релаксации) и темпа изменения давления (скорости изменения равновесного состояния).
Модель (9)–(10) естественным образом обобщается на случай неизотермических процессов (Aglyamova, Indrupskiy, 2019) и переменного общего состава смеси (Богачев и др., 2019).
Найденные неравновесные составы фаз в каждом элементарном объеме (ячейке модели) участвуют в расчете фильтрационных течений через решение системы уравнений неразрывности в стандартной совместной записи, получаемой суммированием уравнений (1)–(2):
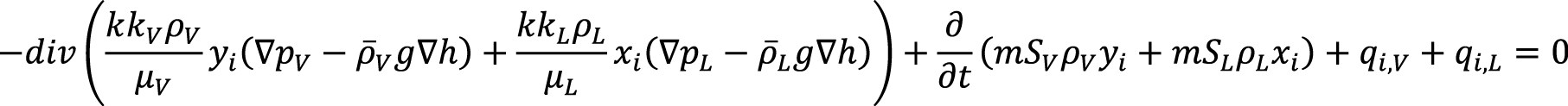 , (11)
, (11)
I = 1,…,N.
В такой постановке модель неравновесного фазового поведения в настоящее время реализована в широко распространенном гидродинамическом симуляторе, с минимальными изменениями программного кода вычислительного ядра по сравнению с равновесным случаем (Богачев и др., 2019).
Особенности применения неравновесных моделей
Возвращаясь к вопросу практического применения моделей неравновесного фазового поведения, необходимо еще раз остановиться на некоторых особенностях проявления неравновесности.
Очевидно, что существенно неравновесное фазовое поведение возникает тогда, когда некоторый дополнительный фактор препятствует фазовым переходам во флюидальной системе и приводит к большим временам установления нового равновесного состояния. Математически учет этого фактора может быть выполнен по-разному на разных масштабах моделирования (Лобанова, Индрупский, 2012; Indrupskiy et al., 2017).
Рассматривая поток вещества между жидкой и газовой фазами на масштабе переноса молекул, немгновенный характер фазового перехода можно учесть с помощью решения уравнений диффузии с учетом расстояния до межфазной границы. В этом случае поведение системы будет соответствовать локально равновесному в каждом элементарном объеме (Saboorian-Jooybari et al., 2014). Однако при моделировании процессов в углеводородной залежи межфазные границы содержатся неявно внутри элементарных объемов, и вместо учета диффузии необходимо перейти к моделированию неравновесного фазового поведения на крупном масштабе.
В этом случае причиной, препятствующей равновесному (мгновенному) фазовому переходу, будет выступать маленький размер (площадь) межфазной границы по сравнению с объемом, содержащим углеводородную смесь. А также другие факторы, препятствующие перемешиванию углеводородных фаз и переходу компонентов через межфазную границу: наличие в порах воды, капиллярные силы, адсорбция и др. Такую неравновесность можно назвать термодинамической (Gorodetskii et al., 2005). Поскольку «движущей силой» для потока компонентов через межфазную границу является разность химических потенциалов, релаксационная модель неравновесных фазовых превращений (9)–(10) (Indrupskiy et al., 2017) хорошо подходит для описания термодинамической неравновесности.
В качестве примера неравновесного фазового поведения углеводородной смеси, обусловленного сегрегацией фаз в локальном объеме, можно привести результаты экспериментов (Лапшин, 2001). Рассматривается обратное испарение ретроградной жидкости, выпавшей из газоконденсатных смесей с различным содержанием компонентов C5+ (рис. 1). Эксперимент предполагал снижение давления в однофазной газообразной системе до полного выпадения жидкой фазы. Затем давление поднимали до пластового (выше точки росы) и фиксировали динамику обратного испарения конденсата. Можно заметить, что чем больше содержание конденсата в системе, тем дольше происходит его переход в газообразное состояние. Отметим, что авторская подпись вертикальной оси на рис. 1 не вполне точная: отложена не доля растворенного конденсата, а ее дополнение до 1, т.е. доля выпавшего конденсата, остающегося в жидкой фазе к текущему моменту времени.
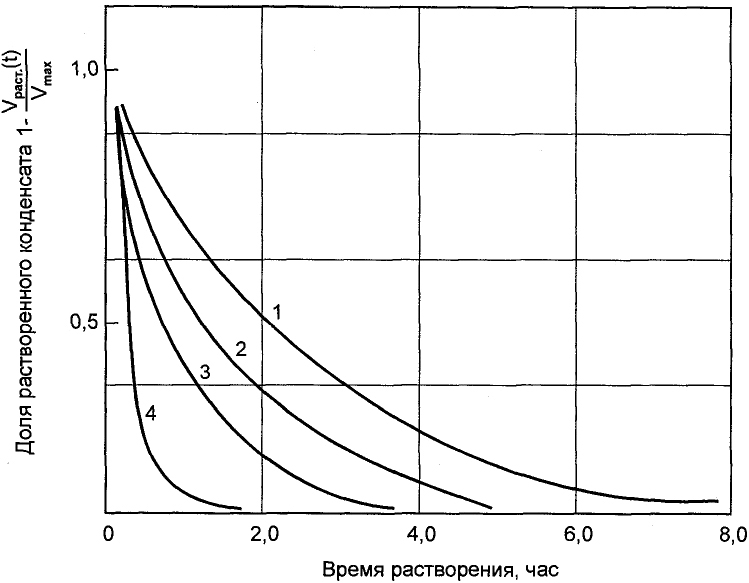
Рис. 1. Динамика испарения жидкой фазы при исследовании газоконденсатных систем с различным содержанием компонентов С5+: 1 – 800 г/м³; 2 – 400 г/м³; 3 – 250 г/м³; 4 – 50 г/м³ (Лапшин, 2001)
В то же время, такая релаксационная модель не позволяет описать неравновесность иного типа, возникающую, например, в экспериментах по дифференциальной конденсации (в ходе процесса истощения) для газоконденсатных систем в ретроградной области (Dorhjie et al., 2025). В этом случае существенные отклонения наблюдаемых долей и составов фаз от равновесных обусловлены высокими скоростями отбора и возникают по той причине, что формирующаяся вторая фаза (капли жидкости) не успевает сегрегироваться и выносится в виде взвеси с потоком основной фазы (газа). Причина несоответствия показателей процессов расчетным равновесным значениям в этом случае не имеет термодинамической природы, поэтому такая неравновесность не может быть описана моделями на основе разности химических потенциалов компонентов в фазах. Для ее моделирования необходимо учитывать соотношение между скоростью роста (изменения радиуса) капель конденсата, темпом их осаждения и интенсивностью выноса с потоком газа. Подобная модель в упрощенном виде рассмотрена в (Чагеева, 2023).
Авторами (Dorhjie et al., 2024) на микромоделях выполнены эксперименты по истощению для газоконденсатной трехкомпонентной смеси метана, бутана и декана в соотношении 0,8325, 0,1125 и 0,055 мольных долей соответственно. Они показали, что использование равновесного термодинамического симулятора на основе уравнения состояния Пенга-Робинсона не позволяет воспроизвести распределение конденсатонасыщенности по длине модели после падения давления ниже точки росы. Причиной отклонения фактических результатов от модельных авторы считают вынос конденсата в виде аэрозоля с потоком газа. Вместо общепринятой концепции профиля насыщения жидкостью газоконденсатного коллектора (рис. 2), ими предложена модель, предполагающая наличие дополнительной зоны между зонами однофазного потока и неподвижного конденсата (рис. 3).

Рис. 2. Общепринятая концепция профиля насыщения жидкостью газоконденсатного коллектора (Dorhjie et al., 2024)

Рис. 3. Концепция профиля насыщения жидкостью газоконденсатных коллекторов с учетом зоны аэрозоля (Dorhjie et al., 2024)
Для прогнозирования профиля насыщенности жидкой фазой с учетом выноса конденсата в виде аэрозоля авторы (Dorhjie et al., 2024) предлагают использовать релаксационный параметр τ в модели материального баланса:
![]() , (12)
, (12)
где Soeos – насыщенность жидкой углеводородной фазой, которая вычисляется с помощью стандартной процедуры расчета фазового равновесия (flash) вместе с газонасыщенностью Sg. Предполагается, что насыщенность жидкой фазой Soeos включает две составляющих: подвижный конденсат в форме аэрозоля с насыщенностью Sofog и неподвижный конденсат с насыщенностью Soeff. Насыщенность неподвижным конденсатом Soeff на некотором шаге i формируется следующим образом. Сначала к насыщенности жидкой фазой Soeos, сконденсированной в локальном объеме (ячейке) на этом шаге, добавляется насыщенность аэрозольным конденсатом Sofog, сформированная на предыдущем шаге i-1 в соседнем объеме и привнесенная с потоком газа. Чтобы учесть, что из этого общего количества конденсата некоторая доля успевает осесть за текущий шаг и сформировать Soeff, авторы (Dorhjie et al., 2024) вводят поправку 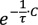 . Оставшаяся часть формирует новую величину Sofog и переносится в соседнюю ячейку.
. Оставшаяся часть формирует новую величину Sofog и переносится в соседнюю ячейку.
При моделировании экспериментов, выполненных на микромоделях пласта, авторы (Dorhjie et al., 2024) предполагают постоянную скорость перемещения аэрозольного конденсата с газовой фазой между ячейками и используют безразмерные координату и время, поэтому шаг по времени Δt = 1 в формулу не включен. C – безразмерный коэффициент силы гидравлического сопротивления, действующей на поток, которая авторами (Dorhjie et al., 2024) в расчетах не учитывалась (принималось C = 1). Отметим, что ряд моментов в формуле (12) выглядят нефизично, в частности, способ применения релаксационной поправки.
Рассмотренные выше особенности использования равновесных и неравновесных моделей схематично показаны на рис. 4 на примере фазового поведения газоконденсатной смеси. В ретроградной области при повышении давления конденсат переходит в газообразное состояние через ограниченную по площади межфазную границу. Такой фазовый переход является неравновесным, поскольку может протекать значительное время, которым на масштабе пластовых процессов нельзя пренебречь (рис. 4а). На рис. 4б показан обратный процесс выпадения конденсата при снижении давления. Такой фазовый переход протекает во всем объеме газовой фазы практически мгновенно по сравнению с темпом снижения давления, поэтому его можно считать равновесным.

Рис. 4. Иллюстрация причин возникновения неравновесного (а) и равновесного (б) фазового поведения без учета и с учетом гидродинамических потоков на примере газоконденсатной смеси
Изменение давления в описанных процессах при разработке залежи обусловлено наличием гидродинамических потоков, учет которых не приводит к изменению природы фазового перехода. В частности, фазовый переход, протекающий при повышении давления в ходе реализации сайклинг процесса (рис. 4а с учетом потока), остается неравновесным. А истощение газоконденсатной залежи с учетом течения к скважинам (рис. 4б с учетом потока) – термодинамически равновесным процессом с возможным выносом капель конденсата в потоке газовой фазы.
Примером ошибочного использования модели (Indrupskiy et al., 2017) является ее применение в работе (Yang et al., 2020) для математического описания экспериментов по истощению газоконденсатной смеси в полноразмерных кернах. На рис. 5 и 6 показаны результаты эксперимента, равновесного и неравновесного моделирования процесса истощения при быстром и медленном снижении давления. Изменение темпа снижения давления, которое авторы трактуют как меру неравновесности фазового поведения, приводит в действительности к изменению интенсивности выноса формирующихся капель конденсата. Авторы же интерпретируют этот процесс как термодинамически неравновесный и ожидаемо приходят к выводу, что применение релаксационной модели не дает значительного улучшения прогнозов по количеству добытого конденсата по сравнению с использованием равновесной модели фазового поведения. Отметим, что помимо выбора несоответствующей модели влияние на такой вывод оказывает и невысокое содержание конденсата в исследуемой смеси.
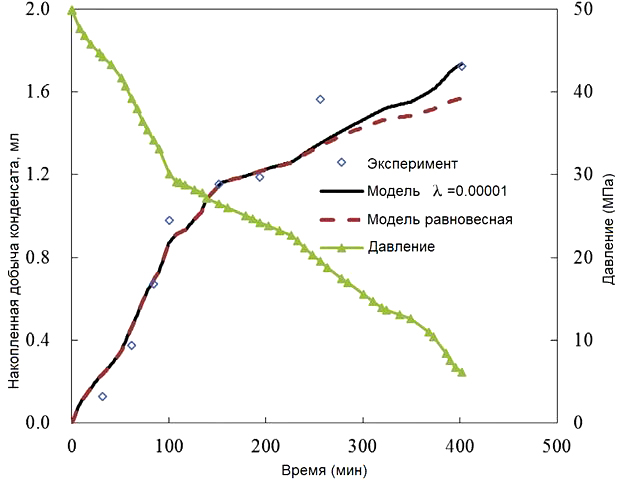
Рис. 5. Добыча конденсата при быстром истощении по результатам эксперимента, равновесного и неравновесного моделирования (Yang et al., 2020)
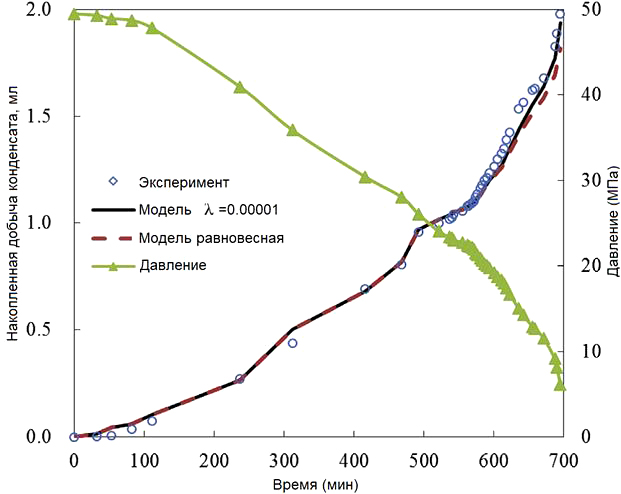
Рис. 6. Добыча конденсата при медленном истощении по результатам эксперимента, равновесного и неравновесного моделирования (Yang et al., 2020)
В (Динариев, Евсеев, 2023) также было проведено моделирование процесса истощения газоконденсатной смеси с учетом неравновесных эффектов для описания течения вблизи вертикальной скважины. Известно, что при этом в околоскважинном пространстве образуется область накопления жидкой фазы – «конденсатная банка». Причем насыщенность пористой среды конденсатом зависит от скорости фильтрации (дебита скважины). Авторы считают, что данное явление обусловлено термодинамически неравновесным выпадением конденсата из газа и может быть описано модификацией традиционной модели (1)–(2). Поскольку матрица кинетических коэффициентов Lij, необходимая для определения интенсивности массопереноса компонентов, может быть получена только экспериментально, авторами предложена методика ее качественной оценки. Для этого элементы матрицы представляются в виде суммы конвективного и диффузионного потоков с некоторым коэффициентом α. Он определяется исходя из геометрии порового пространства и рассматривается как мера проявления неравновесного фазового поведения.
Чтобы оценить правомерность такого подхода, необходимо еще раз остановиться на процессе перехода многокомпонентной системы из однофазного в двухфазное состояние. Ретроградная конденсация при снижении давления ниже точки росы является примером такого процесса. Данный процесс протекает во всем объеме исходной фазы, поэтому он является термодинамически равновесным, что подтверждено лабораторными экспериментами (Gorodetskii et al., 2005).
Пример различного характера прямого и обратного фазовых переходов между однофазным и двухфазным состояниями показан на рис. 7. Приведена P-T диаграмма, полученная в ходе эксперимента по изохорному охлаждению и последующему нагреву трехкомпонентной смеси состава: 50% (мольных) метана, 35% пропана и 15% пентана. Начальная температура 365K, минимальная температура 300K. Процесс охлаждения со скоростью 2K/час показан синей изохорой. Процесс протекает равновесно, излом при температуре 340,6K соответствует равновесному переходу из однофазного в двухфазное состояние. Изохора при нагреве с той же скоростью 2K/час показана оранжевым цветом и является неравновесной. В случае, когда при температуре равновесного фазового перехода 340.6K нагрев останавливали, отмечалась релаксация к равновесному состоянию, показанная красной вертикальной линией.
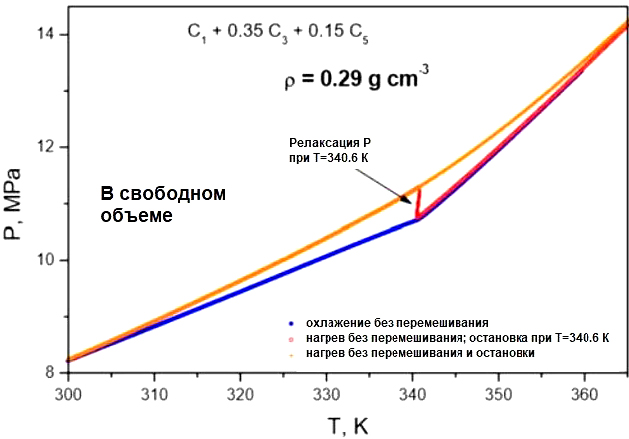
Рис. 7. P-T диаграмма эксперимента с гистерезисом нагрева и охлаждения (Gorodetskii et al., 2005)
В работе (Aglyamova, Indrupskiy, 2019) подтверждено, что полный цикл эксперимента на рис. 7 может быть воспроизведен расчетным путем с применением термодинамически равновесной модели для процесса охлаждения (конденсация) и неравновесной – для процесса нагрева (обратное испарение).
Таким образом, рассматриваемые в работе (Динариев, Евсеев, 2023) эффекты следует объяснять не термодинамически неравновесным выпадением конденсата из газовой фазы, а выносом формирующихся капель конденсата в виде взвеси с потоком газа. Поэтому, аналогично примеру выше, их не следует описывать моделями, основанными на диффузионном переносе вещества и химических потенциалах компонентов.
Остановимся подробнее на влиянии масштаба, на котором описывается фазовое поведение смеси. В (Saboorian-Jooybari et al., 2014) рассматривается вопрос о необходимости использования неравновесной модели при описании диффузии компонентов через границу газ-жидкость, т.е. на мелком масштабе. Авторами выполнены расчеты коэффициентов диффузии с помощью равновесной и неравновесной моделей. При этом относительная погрешность получаемых результатов не превышала 2%. Этот результат можно объяснить, взглянув на формулировку второго закона Фика для описания растворения газа в жидкой фазе:
![]() , (13)
, (13)
где D и C – коэффициент диффузии и массовая концентрация растворенного газа (или отдельного компонента) в жидкости, соответственно.
Данная формулировка описывает некоторый не мгновенный перенос молекул газа от межфазной границы по координате z. Поэтому дополнительное использование неравновесной модели для вычисления коэффициента диффузии не будет иметь значимого эффекта при рассмотрении процесса на мелком масштабе (кроме некоторых особых условий). Иными словами, результаты работы (Saboorian-Jooybari et al., 2014) подтверждают, что второй закон Фика на мелком масштабе позволяет описывать немгновенный фазовый переход без использования неравновесных моделей.
При переходе от мелкого масштаба на осредненный масштаб элементарного объема пласта (ячейки модели) пропадает возможность учета локальной диффузии и зависимости концентраций компонентов от расстояния до межфазной границы. С точки зрения средних составов фаз в ячейке наблюдаемое фазовое поведение интерпретируется как неравновесное и может быть описано рассмотренной выше неравновесной моделью (Лобанова Индрупский, 2012; Indrupskiy et al., 2017).
Примеры практического применения релаксационной модели неравновесных фазовых превращений
Помимо реализации модели (9)–(10) из работы (Indrupskiy et al., 2017), в (Богачев и др., 2019) был предложен альтернативный метод учета неравновесного фазового поведения на основе релаксационной модели. Он предполагает описание процесса релаксации в терминах не разности химических потенциалов, а коэффициентов распределения компонентов (K-значений)
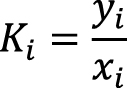 .
.
На очередном шаге по времени в каждом элементарном объеме (ячейке) сначала осуществляется решение системы (8) для определения равновесных K-значений Ki*. Далее рассматривается уравнение релаксации Ki к равновесному значению:
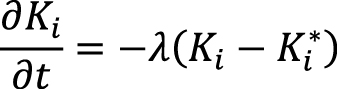 (14)
(14)
с начальным условием, равным значению коэффициента распределения Kin, достигнутому на предыдущем шаге.
Дискретизируя уравнение (14), получают выражение для расчета Ki на следующем шаге:
![]() . (15)
. (15)
По найденным значениям Kin+1 рассчитываются текущие (неравновесные) доли и составы фаз. Отметим, что (15) может быть записано и в нелинеаризованной экспоненциальной форме, аналогично (10).
Данный метод обладает рядом достоинств: высокая вычислительная эффективность и устойчивость, возможность естественного обобщения на неизотермическую композиционную модель. При этом, как и метод работы (Indrupskiy et al., 2017), он требует изменения только алгоритмов расчета фазового состояния системы. Запись уравнений фильтрации не меняется, что дает возможность относительно простой реализации в существующих гидродинамических симуляторах.
В качестве примера практического применения рассматриваемых методов в работе (Богачев и др., 2019) приведены результаты расчетов эксплуатационных характеристик реального газонефтяного месторождения с использованием релаксационной неравновесной модели (Indrupskiy et al., 2017) и модели на основе релаксации К-значений. Композиционная модель флюида состоит из 9 углеводородных компонентов (N2-CH4, CO2, H2S, C2H6, C3H8-C4H10, C5H12-C9H20, C10H22-C19H40, C20H42-C39H80, C40+) и водного компонента. Температура в пласте равна 101.67 °C. Гидродинамическая сетка содержит 900000 блоков, среди которых 180000 – активны. ВНК и ГНК находятся в пределах толщины пласта. Энергия пласта поддерживается за счет закачки воды в области ВНК, а также обратной закачки газа в газовую шапку.
На рис. 8, 9 и 10 приведены графики среднего давления по модели, накопленной добычи нефти и запасов свободного газа в пласте: без учета неравновесных эффектов ([EQ]), а также с учетом неравновесности на основе релаксации разности химических потенциалов с λ = 0.001 сут–1 и λ = 0.01 сут–1 ([0.001] и [0.01] соответственно) и на основе релаксации K-значений с теми же λ ([DKDT 0.001] и [DKDT 0.01] соответственно). Из приведенных графиков видно, что при использовании равновесной модели значения нефтедобычи существенно завышены по сравнению с неравновесными расчетами. Это происходит вследствие мгновенного растворения газа в нефти при превышении давления насыщения, в результате чего уменьшается вязкость нефти и увеличивается ее подвижность. Результаты расчетов с применением релаксационной модели (9)–(10) (Indrupskiy et al., 2017) и модели (15) (Богачев и др., 2019) близки.
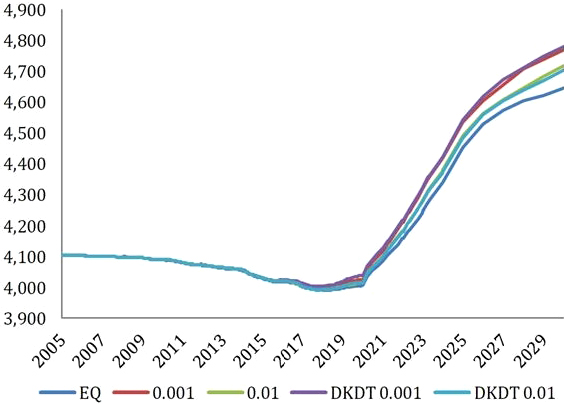
Рис. 8. Динамика среднего давления по модели (в фунтах на квадратный дюйм, Psi) (Богачев и др., 2019)
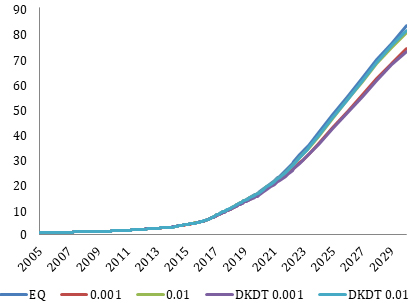
Рис. 9. Динамика накопленной добычи нефти (в млн баррелей при стандартных условиях) (Богачев и др., 2019)
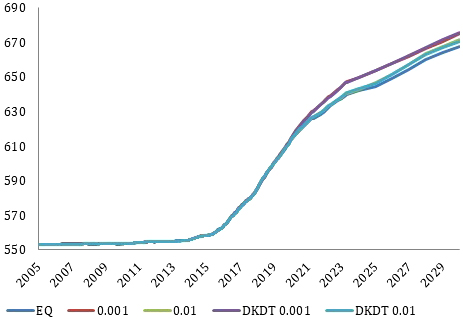
Рис. 10. Запасы свободного газа в пласте (в млрд кубических метров при стандартных условиях) (Богачев и др., 2019)
Отметим, что как показано в (Лобанова и др. 2016; Indrupskiy et al., 2017; Индрупский и др., 2020), величина λ зависит от масштаба моделирования, а использованные значения порядка 10–2–10–3 сут–1 характерны для моделирования работы отдельных скважин или залежи в целом. На практике значение λ является настроечным параметром модели и определяется по результатам адаптации к истории разработки (history matching) и данным промысловых исследований.
Пример существенного влияния неравновесных процессов на показатели разработки реальной нефтегазоконденсатной залежи представлен в работе (Al-Jenaibi et al., 2019). Рассмотрены те же два метода. Продемонстрировано влияние обратного характерного времени релаксации λ на прогнозные динамики добычи углеводородов и изменения давления.
Для фильтрационных моделей типа нелетучей нефти (black oil) аналогом релаксационной модели неравновесных фазовых превращений является модель, основанная на релаксационном уравнении для газосодержания нефти при растворении газа (Зубов и др., 2015).
В модели нелетучей нефти аналогом концентраций компонентов в фазах являются величины газосодержания нефти Rs и, в расширенной формулировке, содержания конденсата в газе Rv. Классическая равновесная постановка предполагает, что при двухфазном состоянии углеводородной смеси газосодержание является функцией давления: Rs = Rs(p). Это означает, что как выделение, так и растворение газа происходит мгновенно вслед за изменением давления. Чтобы учесть немгновенное растворение газа, в коммерческих симуляторах доступна опция ограничения скорости увеличения газосодержания
![]() , (16)
, (16)
где величина D задается в качестве входного параметра и соответствует максимально допустимому изменению газосодержания (в абсолютных единицах) за единицу времени. В работе (Зубов и др., 2015) предложено вместо инженерного соотношения (16) использовать в пределах шага по времени ∆t решение уравнения релаксации для газосодержания в виде:
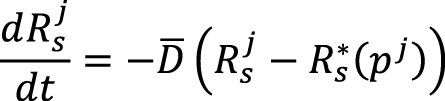 , (17)
, (17)
где ![]() имеет тот же смысл, что и λ в уравнениях (14)–(15), Rs*(p j) – равновесное значение газосодержания при давлении p j. Тогда итоговое выражение для изменения газосодержания на временном шаге имеет вид, аналогичный (15).
имеет тот же смысл, что и λ в уравнениях (14)–(15), Rs*(p j) – равновесное значение газосодержания при давлении p j. Тогда итоговое выражение для изменения газосодержания на временном шаге имеет вид, аналогичный (15).
Пример практического использования и оценки параметров релаксационной модели неравновесных фазовых превращений для случая нелетучей нефти приведен в (Индрупский и др., 2020).
Известно, что выделение растворенного газа в окрестности нефтяной скважины при снижении давления ниже давления насыщения приводит к искривлению индикаторной диаграммы из-за уменьшения фазовой проницаемости для нефти.
Процесс растворения газа при росте давления находит отражение на индикаторной диаграмме обратного хода, которая в таких случаях отличается выраженным гистерезисом. Одной из ключевых его причин является неравновесный (немгновенный) характер обратного фазового перехода углеводородной системы в однофазное состояние. Этот эффект также проявляется при записи кривой восстановления давления (КВД) в виде замедленного выхода кривых давления и его производной на классические режимы (радиальный, линейный и др.), соответствующие течению однофазного флюида.
В качестве примера в (Индрупский и др., 2020) рассмотрена КВД по скважине для залежи сверхлегкой нефти с высоким газосодержанием и давлением насыщения, близким к начальному пластовому давлению. КВД записана в течение около 2 суток после длительной работы на режиме с забойным давлением значительно ниже давления насыщения, что привело к выделению газа и длительному выходу на радиальный режим. Подобный характер кривой не удается воспроизвести в рамках стандартных моделей интерпретации КВД. На рис. 11 показана попытка воспроизведения фактического билогарифмического графика изменения давления и его логарифмической производной модельными кривыми с учетом влияния ствола скважины и зависимости скин-эффекта от дебита. Видно, что на графиках отражены принципиально разные процессы.
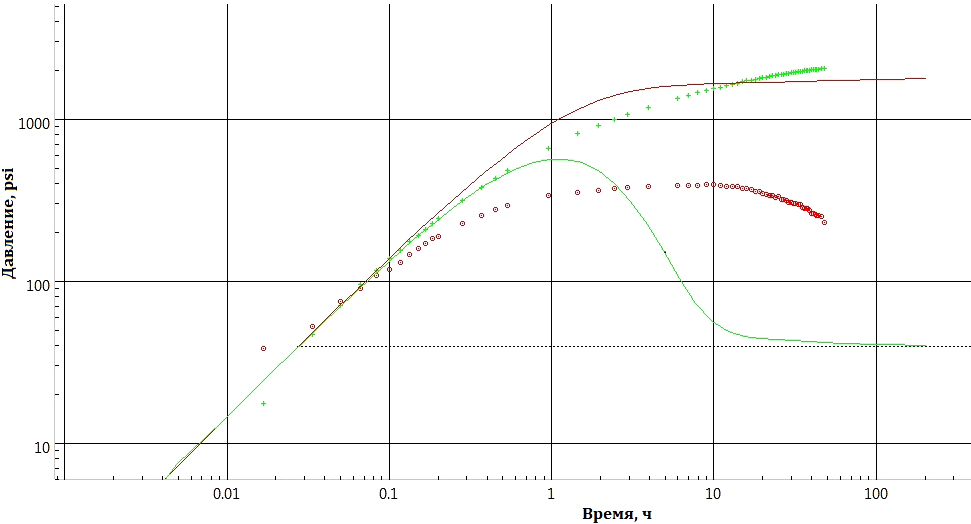
Рис. 11. Модельные (сплошные линии) и фактические (точки) зависимости изменения давления (красная линия, зеленые точки) и его логарифмической производной (зеленая линия, красные точки) от времени в билогарифмических координатах (Индрупский и др., 2020)
Для воспроизведения процессов в пласте с учетом выделения и обратного растворения газа использована слоисто-неоднородная секторная модель области дренирования скважины с возрастающим шагом сетки по горизонтали и параметрами слоев, заданными по результатам интерпретации геофизических исследований скважин.
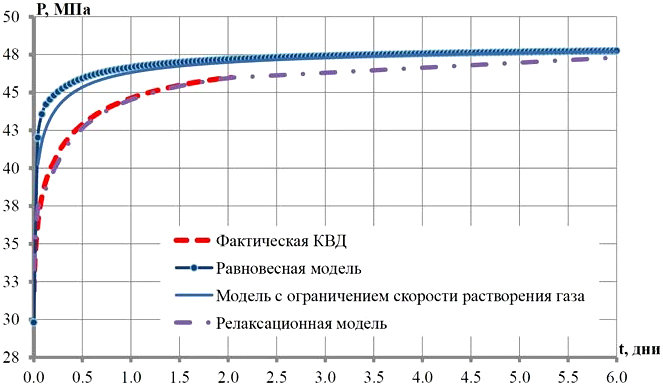
Рис. 12. Результат воспроизведения КВД с помощью релаксационной модели изменения газосодержания при неравновесном растворении газа (Индрупский и др., 2020)
На рис. 12 представлен результат успешного воспроизведения фактической КВД с использованием релаксационной модели изменения газосодержания при неравновесном растворении газа (17) (ключевое слово DRSDTVPE) в сравнении с расчетной кривой по равновесной модели и модели на основе соотношения (16) (ключевое слово DRSDT) с одним из вариантов наилучшей настройки параметра D = 10 м³/м³/сут.
Видно, что методы учета неравновесного фазового поведения углеводородов на основе релаксационной модели позволяют адекватно описывать особенности фазового поведения пластовых флюидов, связанные с недостаточной скоростью массообмена вследствие ограниченной удельной площади сформированной межфазной границы. Т.е. в тех случаях, когда механизм проявления неравновесности является термодинамическим.
В настоящий момент методы учета неравновесного фазового поведения на основе релаксационной модели успешно реализованы в отечественном гидродинамическом симуляторе tNavigator компании RockFlowDynamics как для композиционной модели, так и для модели нелетучей нефти black oil (Rock Flow Dynamics: tNavigator User Manual, 2024).
Особенности моделирования течений флюида с неравновесным фазовым поведением
Как сказано выше, в основе релаксационной модели для учета неравновесных фазовых переходов лежит предположение, что углеводородная система в отсутствие внешнего воздействия стремится к равновесным составам и соотношениям фаз.
Однако при разработке месторождения на этот процесс накладываются внешние воздействия в виде изменений давления (и, возможно, температуры), а также потоков флюидов. Возможны ситуации, при которых равновесные составы и доли фаз не могут быть достигнуты.
Например, при реализации сайклинг-процесса (обратной закачки «сухого» газа в газоконденсатную залежь) необходимо моделировать закачку газа с составом, неравновесным к составу пластовой газоконденсатной смеси. При этом между закачиваемым «сухим» газом и пластовым флюидом происходит интенсивный межфазный массообмен, который стремится привести газовую и жидкую фазы к равновесию. На этот процесс накладывается фильтрация газовой фазы от нагнетательной к добывающей скважине. При этом жидкая фаза остается неподвижной или фильтруется медленнее. В результате фазы равновесного состояния не достигают, причем составы обеих фаз меняются вдоль линии тока.
Для учета неравновесных фазовых превращений, сопровождающихся движением многокомпонентной смеси по пористой среде, неравновесная модель фазового поведения должна быть дополнена переменными, описывающими параметры движения неравновесных фаз.
Авторами работы (Ковалёв, Шеберстов, 2018) выполнено сравнение равновесной композиционной модели (использовался симулятор Schlumberger Eclipse 300), предложенной ими конечно-разностной аппроксимации классической неравновесной модели (Розенберг, Кундин, 1976; Максимов, 1994) и релаксационной неравновесной модели (Indrupskiy et al., 2017), реализованной в симуляторе RFD tNavigator. Для классической неравновесной модели принято одинаковое значение кинетического коэффициента для всех компонентов и ячеек – 5000 г∙моль/сут. Параметр релаксации для релаксационной модели – 0,001 мин–1.
Расчеты выполнены для линейно расположенной системы из девяти ячеек. Граничные условия подобраны так, чтобы моделировать выход системы на стационарный режим. В первой ячейке производится закачка смеси заданного состава, в последней ячейке за счет задания большого фиктивного значения пористости обеспечивается условие заданного давления. Флюидальная система представлена 4х-компонентной смесью СН4, С3Н8, С5Н12, С7Н16. Начальное мольное содержание компонентов соответственно, %: 67–22–8–3. Потенциальное содержание углеводородов С5+ составляет 404,1 г/м³. Давление начала конденсации – 139,2 бар, давление максимальной конденсации – 123,0 бар, максимальная насыщенность конденсатом – 19,37%, температура – 65 °С.
Рассчитан процесс перехода из начального состояния покоя к двухфазной стационарной фильтрации. Изначально модель равновесно инициализирована при давлении 138 бар в двухфазном состоянии. Динамика давления на выходе модели предусматривала равномерное снижение давления до 125 бар в течение 104 мин и поддержание его на этом уровне в дальнейшем.
Сравнительные результаты моделирования приведены на рис. 13. Красным цветом показана динамика насыщенности жидкостью для традиционной неравновесной модели, синим – для равновесной модели, желтым – для релаксационной неравновесной модели.
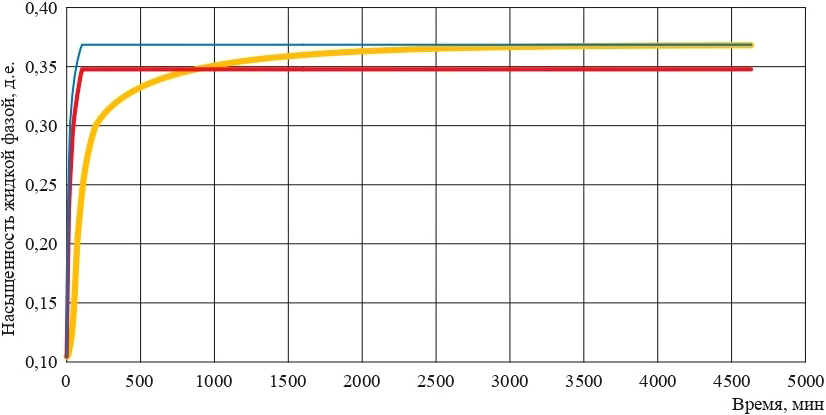
Рис. 13. Динамика насыщенности жидкостью выходной ячейки (Ковалёв, Шеберстов, 2018)
Из рис. 13 видно, что при моделировании фильтрации флюидов с использованием релаксационной модели стационарный режим достигается существенно позже и этот режим является равновесным.
Неизбежность выхода на стационарный режим с равновесным состоянием системы при достаточно длительном процессе следует из записи релаксационной модели (9)–(10) без учета конвективной составляющей производной по времени. В общем случае уравнение релаксации записывается в терминах полной производной:
![]() , (18)
, (18)
где Δi = µi,L - µi,V, и для движущегося элемента флюидальной системы оно принимает вид (Ковалёв, Шеберстов, 2018):
![]() . (19)
. (19)
Однако авторы (Ковалёв, Шеберстов, 2018) оставляют открытым вопрос о расчете скорости переноса w в общем случае фильтрации двухфазной неравновесной смеси.
Следует сказать, что модель, аналогичная (19), успешно используется для описания двухфазных течений в стволах скважин при добыче углеводородов или в процессе бурения. Если в таких моделях речь идет о движении газированной жидкости (модель типа нелетучей нефти), то вопрос выбора скорости в уравнении (19) не стоит. Например, в работе (Tikhonov et al., 2020) предложена модель нестационарного двухфазного течения газонефтяной смеси в скважине с учетом неравновесных фазовых переходов:
![]() , (20)
, (20)
где Θ – характерное время релаксации, x – неравновесная массовая концентрация газового компонента в жидкой фазе, xE – равновесная массовая концентрация газового компонента в жидкой фазе, t – время, s –координата вдоль оси скважины, измеренная от забоя, vl – скорость нефтяной фазы с растворенным газом,
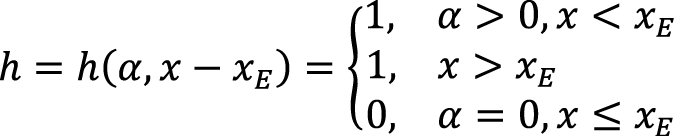
α – объемная доля газовой фазы.
Однако для многомерного течения двухфазной смеси произвольного состава в пористой среде определение скорости переноса в уравнении (19) представляет существенные сложности.
Другим проблемным аспектом учета конвективной составляющей в релаксационной модели является невозможность разделения системы уравнений фильтрации и термодинамической подзадачи (9), которое является важным преимуществом релаксационного метода. Запись релаксационной неравновесной модели с выделением термодинамической подзадачи (9)–(10) (или (9) и (15)) обеспечивает возможность, во-первых, использования вычислительного ядра уже имеющегося программного обеспечения для моделирования равновесной фильтрации. Во-вторых, позволяет проводить расчеты фазового поведения отдельно от фильтрационной подзадачи.
Тем не менее, проблема моделирования фильтрации, сопровождающейся неравновесными фазовыми переходами, действительно требует дальнейшего рассмотрения. Релаксационная модель неравновесного фазового поведения в текущей реализации не предполагает учета конвективной составляющей производной по времени. Однако это не означает, что она принципиально не применима для моделирования реальных фильтрационных течений при разработке месторождений.
Если при наличии фильтрационного потока основополагающим фактором неравновесного фазового поведения является быстрое изменение давления (или температуры), то релаксационная модель может применяться без учета конвективной составляющей. Такая ситуация возникает, например, при повышении давления путем закачки воды в ходе разработки нефтяного месторождения для обратного растворения выделившегося газа (Бриллиант и др., 2014). Или при снижении давления в газоконденсатной залежи ниже давления максимальной конденсации (Лобанова и др., 2016). Если же неравновесное фазовое поведение проявляется преимущественно по причине закачки неравновесных к пластовому флюиду углеводородных смесей (например, при сайклинг-процессе), то влиянием конвективной составляющей, действительно, пренебречь нельзя.
В то же время, при этом возможно сохранение преимуществ релаксационной модели за счет идеи разделения «вложенных» процессов на шаге по времени (Indrupskiy et al., 2017): внешнего (в данном случае влияние фильтрации фаз) и внутреннего (стремление системы к равновесному состоянию). Это может быть сделано за счет введения на каждом временном шаге корректирующих поправок к начальным условиям для релаксационных соотношений вида (10) или (14), вызванных потоком углеводородных компонентов в фазах.
Выводы
Традиционная модель учета неравновесных фазовых превращений при многокомпонентной фильтрации, основанная на раздельной записи уравнений неразрывности компонента в каждой фазе, является наиболее теоретически обоснованной. Однако ее практическое применение представляет затруднения в связи с необходимостью проведения большого объема сложных лабораторных экспериментов для определения параметров межфазного массообмена и их последующего переноса на масштаб течений в пласте. Для реализации традиционной неравновесной модели в существующих гидродинамических симуляторах требуется существенное изменение вычислительного ядра с удвоением размерности системы гидродинамических уравнений.
Релаксационная модель учета неравновесного фазового поведения, основанная на принципе релаксации составов фаз и химических потенциалов компонентов к равновесным значениям, реализуется в существующих гидродинамических симуляторах без принципиальных изменений вычислительного ядра. Модель может быть настроена на фактические данные на масштабе как лабораторных экспериментов, так и реальных процессов разработки залежи, и не требует проведения сложных специализированных экспериментов для определения параметров неравновесности.
В настоящее время накоплен немалый опыт и опубликован ряд примеров практического применения релаксационной модели для описания разработки реальных месторождений углеводородов с неравновесным фазовым поведением, включая оценку параметров модели по данным промысловых исследований.
Как традиционная, так и релаксационная модель описывают термодинамически обусловленные проявления неравновесности. Их применение для корректного воспроизведения фазового поведения и определения его характерных параметров требует правильного понимания природы происходящих процессов. Для описания неравновесных эффектов, обусловленных не термодинамическими причинами, следует использовать модели другого типа.
В общем случае моделирования фильтрации углеводородных флюидов с учетом неравновесных фазовых переходов релаксационная модель на каждом шаге по времени должна быть дополнена корректировкой начальных условий к уравнению релаксации, эквивалентно учитывающих влияние конвективной составляющей полной производной релаксирующей величины по времени.
Финансирование
Работа выполнена в рамках Госзадания ИПНГ РАН, тема 125020501405-1 «Создание новых технологий эффективного экологически чистого извлечения углеводородов в сложных горно-геологических условиях на основе системного подхода к изучению и моделированию полного жизненного цикла нефтегазовых месторождений»
Список литературы
1. Богачев К., Земцов С., Милютин С., Индрупский И., Лобанова О. (2019). Численное моделирование неравновесных фазовых переходов в изотермической композиционной модели фильтрации углеводородов. Российская нефтегазовая техническая конференция SPE, Москва, Россия. SPE-196871-RU.
2. Бриллиант Л.С., Евдощук П.А., Плиткина Ю.А., Антипин М.А., Закиров С.Н., Индрупский И.М., Лобанова О.А. (2014). Возможность эффективной доразработки нефтяных месторождений за счет растворения insitu выделившегося из нефти газа. Нефтяное хозяйство, 4, с. 54–59.
3. Брусиловский А.И. (2002). Фазовые превращения при разработке месторождений нефти и газа. М.: Грааль, 575 с.
4. Булейко В.М., Вовчук Г.А. (2010). Проблема неравновесности в задачах разработки трудноизвлекаемых запасов углеводородов. Вести газовой науки, 5, с. 287–300.
5. Григорьев Е.Б., Сокотущенко В.Н. (2019). Исследование неравновесных изотермических фильтрационных течений углеводородной смеси в пористой среде. Вести газовой науки, 1 (38), с. 93–138.
6. Динариев О.Ю., Евсеев Н.В. (2023). Неравновесные течения газоконденсатной смеси в пористой среде. Прикладная механика и техническая физика, 64(4), с. 130–138. https://doi.org/10.15372/PMTF202315247
7. Зубов В.Р., Индрупский И.М., Богачев К.Ю. (2015). Моделирование обратного растворения газа в моделях BlackOil. Российская нефтегазовая техническая конференция SPE, Москва, Россия. SPE-176618-RU.
8. Индрупский И.М., Данько М.Ю., Цаган-Манджиев Т.Н., Аглямова А.И. (2020). Оценка параметров моделей неравновесного фазового поведения нефтяных и газоконденсатных систем по данным лабораторных и промысловых исследований. Российская нефтегазовая техническая конференция SPE, Москва, Россия. SPE-201956-RU.
9. Ковалёв А.Л., Шеберстов Е.В. (2018). Численное моделирование локально-неравновесной фильтрации в газоконденсатных пластах. Вести газовой науки, 5(37), с. 164–171.
10. Курбанов А.К., Розенберг М.Д., Желтов Ю.П., Шовкринский Г.Ю. (1966). Исследование движения многокомпонентных смесей в пористой среде. Теория и практика добычи нефти: ежегодник ВНИИ. М.: Недра, с. 31–48.
11. Лапшин В.И. (2001). Физическое моделирование фазовых превращений нефтегазоконденсатных систем глубокозалегающих месторождений Прикаспия. Дисс. докт. техн. наук. М., 329 с.
12. Лобанова О.А., Зубов В.Р., Индрупский И.М. (2014). Неравновесное фазовое поведение углеводородных смесей. Часть 1: эксперименты. Автоматизация, телемеханизация и связь в нефтяной промышленности, 11, с. 18–23.
13. Лобанова О.А., Индрупский И.М. (2012). Неравновесные и масштабные эффекты в моделировании фазового поведения углеводородных смесей. Нефтяное хозяйство, 6, с. 49–53.
14. Лобанова О.А., Индрупский И.М., Ющенко Т.C. (2016). Моделирование неравновесной динамики конденсатоотдачи на поздней стадии разработки газоконденсатной залежи. Российская нефтегазовая техническая конференция SPE, Москва, Россия. SPE-181977-RU. https://doi.org/10.2118/181977-RU
15. Максимов В.М. (1994). Основы гидротермодинамики пластовых систем. М.: Недра, 201 с.
16. Розенберг М.Д., Кундин С.А. (1976). Многофазная многокомпонентная фильтрация при добыче нефти и газа. М.: Недра, 335 с.
17. Чагеева П.А. (2023). Исследование критериев неравновесного фазового поведения. Магистерская диссертация. РГУ Нефти и Газа им. Губкина, 44 с.
18. Aglyamova A.I., Indrupskiy I.M. (2019). Numerical simulation of non-equilibrium isochoric phase transitions in hydrocarbon mixtures. IOP Journal of Physics: Conference Series, 1391, 012149. https://doi.org/10.1088/1742-6596/1391/1/012149
19. Al-Jenaibi F., Bogachev K., Milyutin S., Zemtsov S., Gusarov E., Kuzevanov M., Indrupskiy I. (2019). Numerical Simulation of Non-Equilibrium Phase Behavior of Hydrocarbons for Modeling Oil and Gas Fields with Gas Injection. SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE. SPE-196633-MS. https://doi.org/10.2118/196633-MS
20. Dorhjie D.B., Aminev T., Gimazov A., Khamidullin D., Kuporosov D., Maerle K., Grishin P., Cheremisin A. (2025). Impact of depletion rate on the thermodynamics of gas condensates: Experimental insights and analysis. Gas Science and Engineering, 134, 205534. https://doi.org/10.1016/j.jgsce.2024.205534
21. Dorhjie D. B., Pereponov D., Aminev T., Gimazov A., Khamidullin D., Kuporosov D., Tarkhov M., Rykov A., Filippov I., Mukhina E., Shilov E., Grishin P., Cheremisin A. (2024). A Microfuidic and Numerical Analysis of Non equilibrium Phase Behavior of Gas Condensates. Scientific Reports 14, 9500. https://doi.org/10.1038/s41598-024-59972-x
22. Gorodetskii, E.E., Voronov, V.P., Muratov, A.R., Kulikov, V.D. (2005). Study of Non-Equilibrium Phase Transitions in Binary and Ternary Hydrocarbon Mixtures. Research Report. Moscow, OGRI RAS.
23. Indrupskiy I.M., Lobanova O.A., Zubov V.R. (2017). Non-equilibrium phase behavior of hydrocarbons in compositional simulations and upscaling. Computational Geosciences, 21(5), рр. 1173–1188. DOI: 10.1007/ s10596-017-9648-x
24. Mohamadi-Baghmolaei M., Azin R., Osfouri S., Zendehboudi S. (2019). Evaluation of mass transfer coefficient for gas condensates in porous systems: Experimental and modeling. Fuel, 255, 115507. https://doi.org/10.1016/j.fuel.2019.05.090
25. Nghiem L.X., Sammon P.H. (1997). A Non-Equilibrium Equation-of-State Compositional Simulator. SPE Reservoir Simulation Symposium, Dallas, USA. SPE 37980.
26. Rock Flow Dynamics: tNavigator User Manual (2024). Version 23.4.
27. Saboorian-Jooybari H., Dejam M., Chen Z. (2014). Equilibrium or Nonequilibrium Models: A Critical Issue in Determination of Gas Diffusivity in Oil. SPE Heavy Oil Conference, Calgary, Canada. SPE-170030-MS. https://doi.org/10.2118/170030-MS
28. Tikhonov V.S., Indrupskiy I.M., Bukashkina O.S. (2020). Effects of phase transitions on nonstationary liquid-gas flow in a well during gas kicks. Journal of Petroleum Science and Engineering, 184, 106526. https://doi.org/10.1016/j.petrol.2019.106526
29. Whitson C.H., Brule M.R. (2000). Phase Behavior. SPE Monograph (Henry L. Doherty) Series, 20, SPE, Richardson, USA, 233 p. https://doi.org/10.2118/9781555630874
30. Yang Y., Lun Z., Wang R., Hu W. (2020). Non-equilibrium phase behavior in gas condensate depletion experiments. Fluid Phase Equilibria, 506, 112410. https://doi.org/10.1016/j.fluid.2019.112410
Об авторах
О. А. ЛобановаРоссия
Ольга Андреевна Лобанова – кандидат тех. наук, научный сотрудник
119333, Москва, ул. Губкина, д. 3
И. М. Индрупский
Россия
Илья Михайлович Индрупский – доктор тех. наук, главный научный сотрудник, заместитель директора по научной работе
119333, Москва, ул. Губкина, д. 3
Рецензия
Для цитирования:
Лобанова О.А., Индрупский И.М. Особенности применения моделей неравновесного фазового поведения в задачах разработки месторождений углеводородов: критический обзор. Георесурсы. 2025;27(3):252-266. https://doi.org/10.18599/grs.2025.3.17
For citation:
Lobanova O.A., Indrupskiy I.M. Application specifics of nonequilibrium phase behavior models in the development of hydrocarbon deposits: a critical review. Georesursy = Georesources. 2025;27(3):252-266. (In Russ.) https://doi.org/10.18599/grs.2025.3.17















.png)


