Перейти к:
Влияние параметров течения реакционного флюида на скорость растворения породы коллектора
https://doi.org/10.18599/grs.2025.2.16
Аннотация
Метод цифрового анализа керна (и связанные с ним инструменты прямого моделирования течения в поровых каналах) предоставляет уникальные возможности для моделирования физико-химических процессов на микроуровне с учетом структуры и свойств минеральной матрицы реальных породколлекторов. В статье представлены результаты численного моделирования кислотной обработки карбонатных коллекторов на поровом уровне с использованием метода функционала плотности для гидродинамики (DFH). В рамках предложенного подхода взаимодействие потока раствора соляной кислоты (HCl) с поверхностью пор учитывается посредством введения дополнительного потенциала, зависящего от расстояния до поверхности. Исследование направлено на изучение влияния скорости закачки кислотного раствора на эффективность растворения минеральной матрицы, изменение пористости и проницаемости породы. Моделирование проводилось на трехмерной цифровой модели доломита, реконструированной по данным рентгеновской томографии. Учет гетерогенности порового пространства и химических реакций на поверхности минерала позволил исследовать влияние режимов течения на процесс растворения минеральной матрицы и получить эмпирические зависимости скорости эффективной реакции от скорости потока. Результаты работы демонстрируют высокий потенциал применения численных методов для изучения процессов, которые трудно или невозможно воспроизвести в лабораторных условиях. Предложенный подход открывает новые перспективы для анализа воздействия кислотных растворов на фильтрационно-емкостные характеристики пород-коллекторов, что имеет важное значение для повышения эффективности разработки месторождений углеводородов.
Для цитирования:
Иванов Е.Н., Коробков Д.А., Стукан М.Р. Влияние параметров течения реакционного флюида на скорость растворения породы коллектора. Георесурсы. 2025;27(2):206–215. https://doi.org/10.18599/grs.2025.2.16
For citation:
Ivanov E.N., Korobkov D.A., Stukan M.R. Influence of the Reactive Fluid Flow Regime on Mineral Dissolution Rate. Georesursy = Georesources. 2025;27(2):206–215. (In Russ.) https://doi.org/10.18599/grs.2025.2.16
Введение
Кислотная обработка (КО) является широко применяемым методом интенсификации добычи углеводородов, используемым как на нефтяных, так и на газовых месторождениях. Эффект достигается за счет частичного растворения минеральной матрицы породы кислотным раствором, который закачивается в пласт под давлением, не превышающим давление разрыва. Наблюдающиеся при этом паттерны растворения минеральной матрицы могут существенно варьироваться в зависимости от типа породы, состава кислотного раствора и скорости закачки. При низких скоростях закачки происходит равномерное растворение породы в прискважинной области, так как кислота расходуется до проникновения вглубь пласта. В случае высоких скоростей закачки растворение происходит во всем объеме проникновения кислоты, что приводит к равномерному увеличению пористости породы. Однако наиболее эффективным с экономической точки зрения является вариант формирования вблизи скважины сети тонких каналов, известных как червоточины, что происходит при промежуточных скоростях закачки. Таким образом, определение оптимальной скорости закачки является ключевой задачей для успешного проведения кислотной обработки.
Для эффективного применения КО необходимо наличие комплексной информации о геологических, гидродинамических и химических характеристиках коллектора, включая параметры взаимодействия минералов породы с закачиваемыми кислотными растворами. Однако традиционные лабораторные методы не позволяют определить весь набор необходимых параметров, особенно в случае гетерогенной пористой среды. Ключевая проблема заключается в невозможности подбора идентичных образцов породы для тестирования различных кислотных составов, что ограничивает интерпретацию и валидность получаемых результатов. В силу этого сложно переоценить возможность определять необходимые характеристики из моделирования процессов на поровом уровне и последующего их масштабирования на модели меньшего разрешения, такие как, например, модель Дарси.
Развитие вычислительных мощностей и методов численного моделирования открыло новые возможности для планирования и оптимизации кислотной обработки. На сегодняшний день разработан ряд подходов и симуляторов (Glasbergen et al., 2009; Steefel et al., 2015; Qiu et al., 2018; Ali, Nasr-El-Din, 2020), которые используются для моделирования КО. Однако при внимательном анализе (Beletskaya et al., 2017) обнаруживается, что большинство существующих моделей не обеспечивают достаточной точности в предсказании оптимальных параметров обработки. Одной из возможных причин является используемое в промышленных моделях предположение об идеальном (равномерном) смешении минералов и флюида на масштабах, меньших размера дискретизации, что исключает какое-либо влияние на результат структурной неоднородности порового пространства. В то же время, было показано (Dubetz et al., 2016; Etten et al., 2015; Ziauddin, Bize, 2007; Lisitsa et al., 2020), что распределение пор по размерам и их структура оказывают, в некоторых случаях, большее влияние на эффективность кислотной обработки, чем пористость и проницаемость. Таким образом, изучение всего комплекса химических и гидродинамических процессов на поровом уровне является важной задачей для повышения точности прогнозирования результатов КО.
В настоящее время существует целый ряд подходов, позволяющих проводить моделирование течения на поровом уровне. Например, решеточный метод Больцмана (Wolf-Gladrow, 2000), метод сглаженных частиц (Gingold, Monaghan, 1977), метод связанных поровых каналов (Kim, Lindquist, 2012) и методы вычислительной гидродинамики (Chung, 2002). Однако ни один из вышеперечисленных методов не способен адекватно учитывать растворение и/или осаждение, что затрудняет моделирование процессов, связанных с изменениями поровой структуры, и описание взаимосвязи химических реакций с переносом вещества.
Эффективная скорость гетерогенной реакции (количество растворенного минерала в единице объема породы за единицу времени) в пористой среде зависит от скорости потока (Beletskaya et al., 2017; Gautelier, 1999). Высокие скорости потока способствуют перемешиванию компонентов у поверхности породы, таким образом, увеличивая скорость реакции до кинетического предела. Напротив, при низких скоростях флюида скорость реакции ограничивается переносом кислоты к зоне реакции. При этом в большинстве численных моделей для оптимизации КО предполагается условие идеального смешения, что соответствует плато на зависимости эффективной скорости реакции от скорости потока (Beletskaya et al., 2017), когда эффективная скорость реакции считается постоянной и определяется кинетикой реакции на поверхности породы. Однако такое упрощение не позволяет учитывать реальную структуру порового пространства, что снижает точность прогнозов.
Ранее (Beletskaya et al., 2017) нами была предложена и реализована модель взаимодействия реагирующего флюида с минеральной матрицей породы на масштабе пор, основанная на методе функционала плотности для гидродинамики (DFH). Этот подход позволил учесть разнообразные химические и физические процессы, происходящие на микроуровне. В настоящей работе мы применили данный метод для изучения влияния режимов течения на эффективность растворения породы и определения зависимости эффективной скорости реакции от скорости потока с учетом реальной поровой структуры.
Описание модели
В данной работе был применен метод прямого моделирования течения химически активного раствора в микроструктуре реальной породы. Этот метод был первоначально разработан для двумерной постановки (Beletskaya et al., 2017) и впоследствии расширен для работы с более сложными трехмерными моделями пористой среды (Ivanov et al., 2020). Данный подход позволяет качественно воспроизводить такие ключевые процессы, как диффузия компонентов раствора к зоне реакции и химические реакции на поверхности минеральной матрицы. При этом изменения как структуры минеральной фазы, так и распределения компонентов раствора осуществляются совместно с моделированием течения флюида.
Ниже приведено краткое описание метода функционала плотности для гидродинамики (DFH), а также композиционной модели флюида и модели породы, которые были использованы для проведения расчетов в рамках настоящего исследования.
Функционал плотности для гидродинамики с химическими реакциями
В основе подхода к моделированию, использованного в данной работе, лежит интеграция принципов химической кинетики, термодинамики и теории функционала плотности, адаптированной для задач гидродинамики. Этот метод был разработан для моделирования многофазных течений с учетом сложных физико-химических процессов. Он универсален и не ограничен конкретным типом закачиваемого флюида или породы, что позволяет применять его для моделирования жидкостей со сложной реологией, таких как полимерные растворы или эмульсии.
Теория функционала плотности в композиционной гидродинамике, подробно описанная в работах (Demianov et al., 2011; Demianov et al., 2014), базируется на представлении системы через функционал энергии, зависящий от распределения мольных плотностей отдельных компонентов. Этот подход аналогичен широко известному методу функционала плотности, используемому в квантово-химических расчетах, где состояние системы описывается функционалом электронной плотности. Ниже, без детального вывода, кратко изложены основные положения теории функционала плотности для изотермического случая, который является достаточным для большинства практических приложений и использовался в данной работе.
Прежде чем перейти к основным уравнениям, определим ключевые переменные, описывающие состояние среды в каждый момент времени t. Это мольные плотности компонентов ni и компоненты скорости массопереноса ua. Здесь индексом i обозначен номер компонента (i = 1,…,M), а индексы a и b соответствуют одной из декартовых координат: x, y или z. Для обозначения частных производных по координате и времени используется сокращенное обозначение
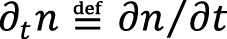 .
.
Также везде подразумевается суммирование по дважды повторяющимся индексам (например,
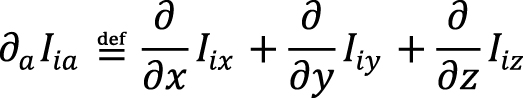 ).
).
В отличие от других подходов, применяемых в гидродинамике, в методе функционала плотности для описания многофазной изотермической системы используется термодинамический потенциал свободной энергии Гельмгольца:
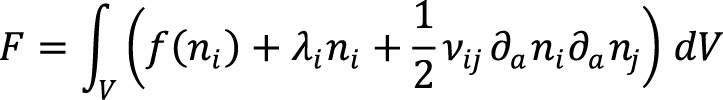 , (1)
, (1)
где V – рассматриваемая пространственная область; f – удельная свободная энергия Гельмгольца на единицу объема однородной смеси; li = li(x,y,z) – распределение потенциала внешних сил, действующих на частицы i-ого компонента. Хотя в общем случае матрица коэффициентов vij может зависеть от локальных мольных плотностей, в применении к рассматриваемой задаче она принимается постоянной и диагональной: vij = v*dij.
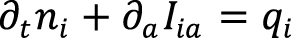 , (2)
, (2)
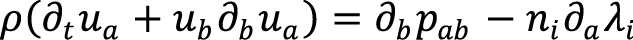 . (3)
. (3)
Здесь qi – скорость изменения мольной плотности i-ого компонента в результате химических реакций, pab – тензор напряжений. Поток Iia может быть представлен как сумма массопереноса и диффузионного потока Qia:
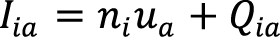 .
.
Потоки отдельных компонентов используются для расчета общего потока Ia, массовой плотности r и среднемассовой скорости ua:
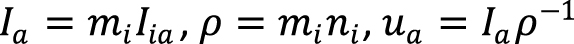 ,
,
где mi – молярная масса i-ого компонента. По определению, диффузионный поток не влияет на общий массоперенос:
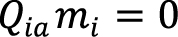 .
.
Замыкающими соотношениями для уравнений гидродинамики (2, 3) служат явные выражения для потоков компонентов Qia, тензора напряжений pab и скоростей химических реакций qi. Диффузионный поток и тензор напряжений определяются через функционал свободной энергии следующим образом:
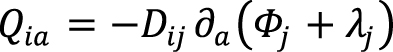 ,
,
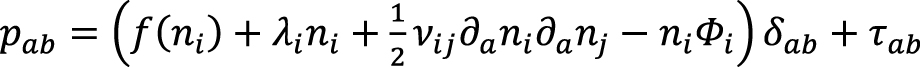 ,
,
где Фi – обобщенный химический потенциал i-го компонента, вычисляемый с помощью вариационной производной от функционала (1):
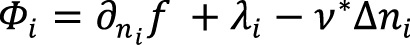 ;
;
Dij– положительно определенная матрица коэффициентов многокомпонентной диффузии; tab – тензор вязких напряжений и dab – символ Кронекера. Матрица Dij строится таким образом, чтобы эффективный молекулярный коэффициент диффузии в условиях численного эксперимента для заданного компонента совпадал с экспериментально определенным коэффициентом диффузии, а матрица диффузии в целом удовлетворяла условию нулевого массопереноса.
Функция f определяет свойства однородной смеси компонентов. В случае однофазного потока с химическими реакциями вид функции свободной энергии имеет следующий вид (Beletskaya et al., 2017):
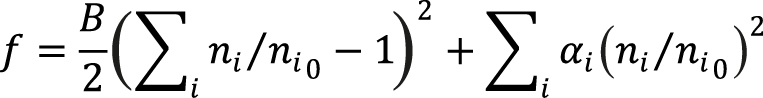 , (4)
, (4)
где B – объемный модуль упругости раствора; ni0 = (vi0)–1 – обратные молярные объемы компонентов реакционного флюида; ai – модельные параметры, настраиваемые по известным свойствам раствора. Для упрощения вычислений используется метод псевдокомпонентов, позволяющий уменьшить количество независимых уравнений и переменных. Таким образом, свойства компонентов в уравнении (4) являются настраиваемыми параметрами.
Учет геометрии поверхности пор
Для моделирования потока без химических реакций достаточно задать геометрию породы и граничные условия для потоков и плотностей на поверхностях раздела флюида и породы, при этом внутренние области твердой матрицы исключаются из рассмотрения. Чтобы расширить метод функционала плотности на случай с химическими реакциями был разработан новый подход к описанию взаимодействия между жидкой и твердой фазами (Beletskaya et al., 2017), включающий: 1) описание механизма взаимодействия на границах раздела жидкой фазы и минерала и 2) определение закона изменения геометрии твердой фазы в зонах контакта с реакционным флюидом.
Для этого в расчетах на поровом уровне было введено распределение потенциалов внешних сил li (x,y,z), зависящее от расстояния D до поверхности поры li = li(D(x,y,z)) и определяющее область пор, где на флюид действуют отталкивающие силы:
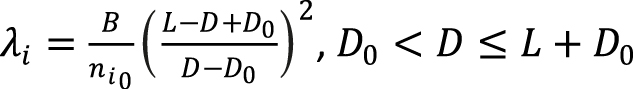 .
.
Здесь L – радиус действия потенциала, а D0 < − L/2 глубина (при движении внутрь по нормали к поверхности поры), на которой потенциал стремится к бесконечности (внутри минерального скелета расстояния считаются отрицательными).
В процессе растворения породы величина потенциального поля li (x,y,z) во всем объеме модели постепенно уменьшается, поскольку расстояние до ближайшей поверхности поры постоянно увеличивается. Это продолжается до тех пор, пока порода в ячейках не будет полностью растворена. Для корректного учета этого процесса необходимо постоянно пересчитывать расстояния до поверхности пор на основе распределения мольной плотности минерала. Хотя геометрический метод позволяет определить расстояния во всем объеме поровой модели после ее сегментации на области пор и минерального скелета, на практике, для оптимизации расчетов расстояния вычисляются только вблизи поверхности пор, где внешние силы, действующие на флюид, существенно отличаются от нуля. Что включает как пространство внутри пор, так и области на небольшом удалении вглубь от поверхности минерального скелета, куда флюид может проникать под действием внешних сил. Такой подход позволяет эффективно разделять расчеты расстояний в различных областях, исключая влияние удаленных границ.
Таким образом, потенциалы внешних сил определены в тонком слое толщиной L вблизи поверхности породы и быстро убывают с расстоянием от границы (рис. 1). Они заменяют в уравнениях гидродинамики распределения плотности твердой фазы. При этом при движении вглубь скелета потенциал плавно растет, позволяя флюиду проникать на небольшую глубину (D0 + L/2) внутрь твердой фазы. Именно в этой области перекрытия мольных плотностей флюида и минерала определена химическая реакция.
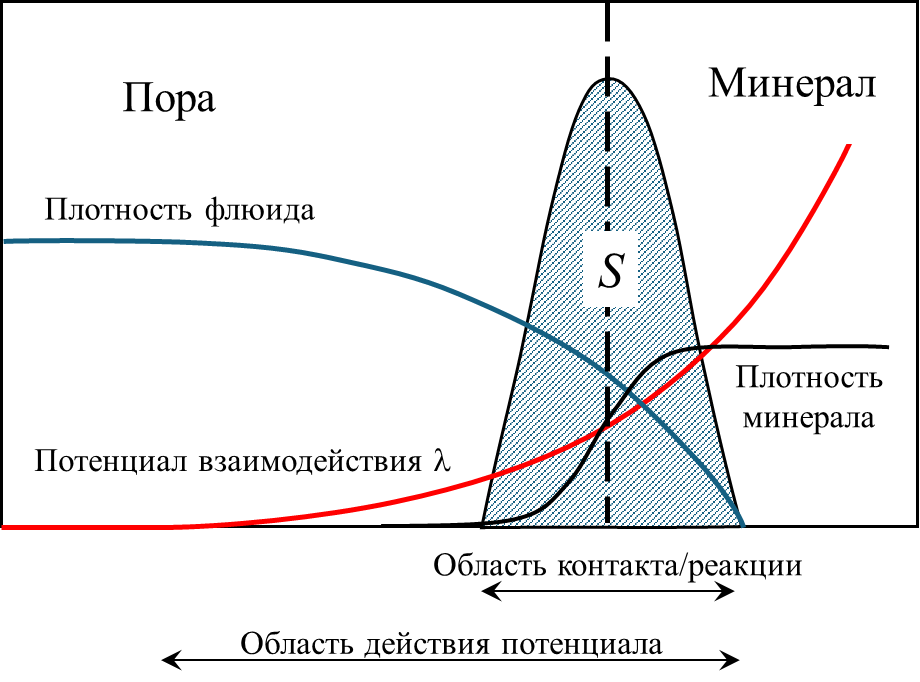
Рис. 1. Схема граничного слоя вблизи поверхности твердой фазы. Выделено распределение удельной площади поверхности S вблизи стенки.
Химическая реакция на поверхности минерала
Химические реакции были включены в гидродинамические расчеты в предположении частичного локального равновесия (Sevougian et al., 1995). Этот подход предполагает описание медленных реакций посредством уравнений химической кинетики, в то время как быстрые реакции считаются мгновенно достигающими равновесия. Такое упрощение позволяет значительно сократить количество химических компонентов и уравнений реакций, которые необходимо учитывать в уравнениях сохранения массы. Данный метод представления сложных химических реакций успешно применялся как для моделирования процессов фильтрации (Ziauddin, Robert, 2003), так и для расчетов на поровом уровне (Beletskaya et al., 2017). В рамках указанного подхода широкий спектр реальных химических реакций заменяется ограниченным набором эффективных реакций, выраженных через концентрации псевдокомпонентов. В данной работе в качестве таких псевдокомпонентов рассматриваются вода, минерал, кислота и продукты реакции. В дальнейшем в уравнениях гидродинамики (2, 3) учитываются только эти эффективные реакции.
На масштабе пор реакции представляют собой гетерогенный процесс, протекающий на поверхности раздела флюид-порода. Локальные скорости изменения плотности псевдокомпонентов qi, вызванные химическими реакциями, рассчитываются через вектор стехиометрических коэффициентов реакции hi и кинетические законы реакции с заданными параметрами.
Для реализации описанного подхода необходимо определить скорости эффективных реакций. В данной работе рассматривался процесс растворения доломита, для которого реакция растворения в кислотной среде зависит от активности H+ (Busenberg, Plummer, 1982):
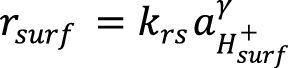 , (5)
, (5)
где krs – константа поверхностной скорости реакции, зависящая от температуры [моль·м–2·с–1],
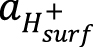 – активность ионов водорода около поверхности минерала, а g – порядок реакции.
– активность ионов водорода около поверхности минерала, а g – порядок реакции.
Таким образом, с учетом ограничения на описание процесса растворения в терминах эффективных реакций и принимая во внимание тот факт, что активность ионов водорода связана с концентрацией кислоты, было использовано следующее выражение для скорости изменения локальной плотности компонентов на границе раздела реакционный флюид - минерал:
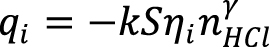 , (6)
, (6)
где nHCl – концентрация (молярная плотность) псевдокомпонента «кислота»; S – удельная площадь поверхности породы, внутри которой проходит граница раздела флюид-порода; hI – вектор стехиометрических коэффициентов реакции (отрицательные для реагентов, положительные для продуктов реакции).
Согласно данному выше определению пограничного слоя, площадь поверхности минерала задается гладкой функцией, определенной в тонкой трехмерной области вблизи поверхности раздела флюид-порода. Форма распределения этой функции зависит от плотности породы и должна быть калибрована на основе результатов простых одно- и двухмерных расчетов, чтобы точно воспроизводить эффективную скорость реакции на плоской поверхности с известными свойствами. В случае сложной трехмерной геометрии постепенно растворяющейся породы, точное определение актуальной площади поверхности представляет собой сложную и ресурсоемкую задачу. Однако на практике достаточно воспроизвести общий тренд изменения параметров, используя корреляции или подсчитывая количество ячеек, содержащих границы раздела флюид-порода.
В настоящей работе удельная площадь поверхности задавалась функцией, пропорциональной локальному модулю градиента плотности минерала, и нормировалась на общее значение, определенное для породы в целом. Такой подход позволяет эффективно учитывать изменение площади поверхности породы в процессе растворения, сохраняя вычислительную эффективность модели.
Цифровая модель породы
В текущем исследовании в качестве породы рассматривался доломит. Трехмерные цифровые модели породы были построены путем реконструкции изображений, полученных методом рентгеновской томографии цилиндрического образца породы (8 мм в диаметре) с высоким разрешением ~2,5 мкм/пиксель, позволяющим восстановить структуру порового пространства. Изображение высокого разрешения 8 мм образца было использовано для выбора кубической микромодели размером 3003 вокселей. Эта модель была затем использована для моделирования растворения породы потоком реакционного флюида. На рис. 2 представлены изображения среза 8-миллиметрового образца доломита и соответствующей микромодели. Светлые области соответствуют зонам с высоким поглощением рентгеновских лучей – минералам, тогда как темные участки представляют поровое пространство. Для наглядности на изображении показан масштаб микромодели относительно 8-миллиметрового образца.
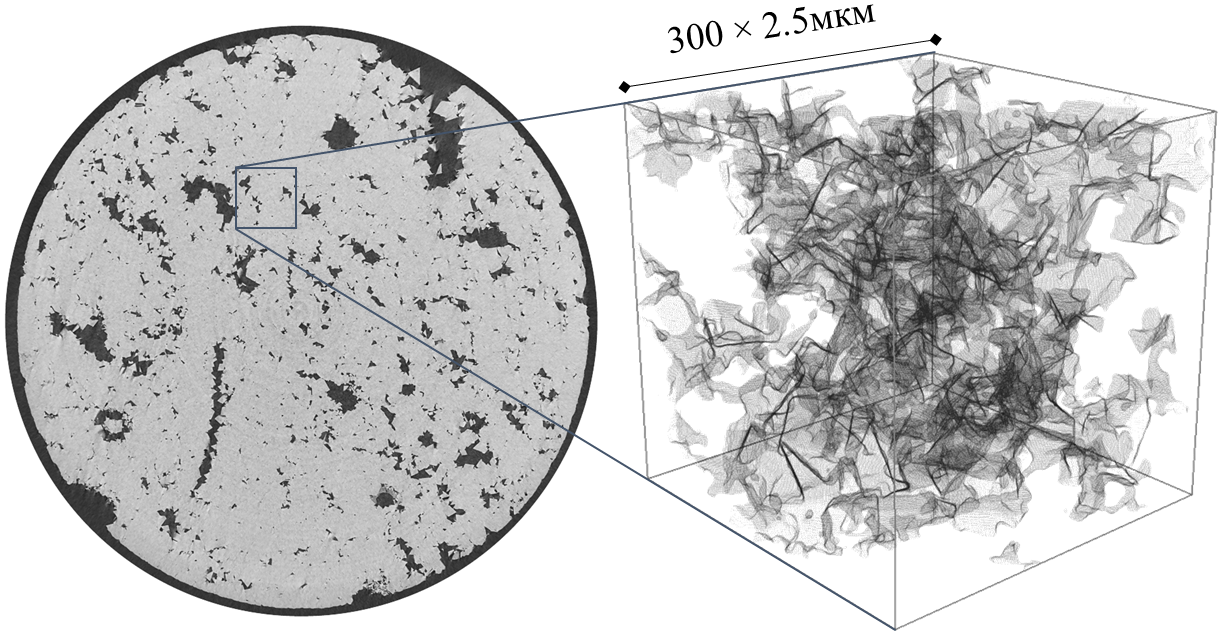
Рис. 2. Срез сегментированного изображения 8-миллиметрового образца доломита (в оттенках серого показана плотность минеральной матрицы, поры черные), и выбранная кубическая модель, использованная для моделирования течения реакционного флюида в порах (минеральная матрица не показана, поры прозрачные серые с выделением поверхности).
Свойства микромодели были определены на основе анализа изображения и моделирования однофазного течения. Пористость модели составила Кп0 = 20,1%, а проницаемость Кпр0 = 450 мД. Параметры моделирования, включая свойства флюида, характеристики взаимодействия кислоты с доломитом и скорость диффузионного переноса компонентов в растворе, были выбраны на основе известных табличных значений или путем калибровки модели на экспериментальные данные (Ivanov et al., 2020).
Результаты моделирования и их анализ
Моделирование потока реакционного флюида в породе для различных скоростей течения было выполнено на модели, представленной на рис. 2. Постановка численного эксперимента соответствовала использованной ранее при исследовании транспортных характеристик пород (Ivanov et al., 2014; Klemin et al., 2015).
В каждом расчете 15%-ный водный раствор соляной кислоты закачивался через нижнюю грань модели при постоянном перепаде давления. На противоположной стороне давление поддерживалось постоянным на уровне, достаточном для предотвращения образования газовой фазы. Остальные границы модели были заданы как непроницаемые. Скорость течения реакционного флюида определялась величиной перепада давления.
В базовом варианте перепад давления составлял 1750 Бар/м, что обеспечивало режим течения, соответствующий равномерному растворению породы во всем объеме модели. Размер модели (300³ ячеек) не позволял напрямую воспроизвести переход от режима равномерного растворения к формированию каналов и растворению внешней поверхности. Поэтому вариант с медленным растворением породы и относительно высокой скоростью течения раствора кислоты был выбран в качестве базового для калибровки модели.
На рис. 3 представлены результаты моделирования потока раствора кислоты в порах при закачке до 11 поровых объемов исходной модели (распределение кислоты показано в желто-зеленых тонах, продуктов реакции в красно-фиолетовых). После закачки первых 1–1,5 поровых объемов кислота заполняет большую часть доступных каналов, и её распределение в дальнейшем изменяется незначительно.
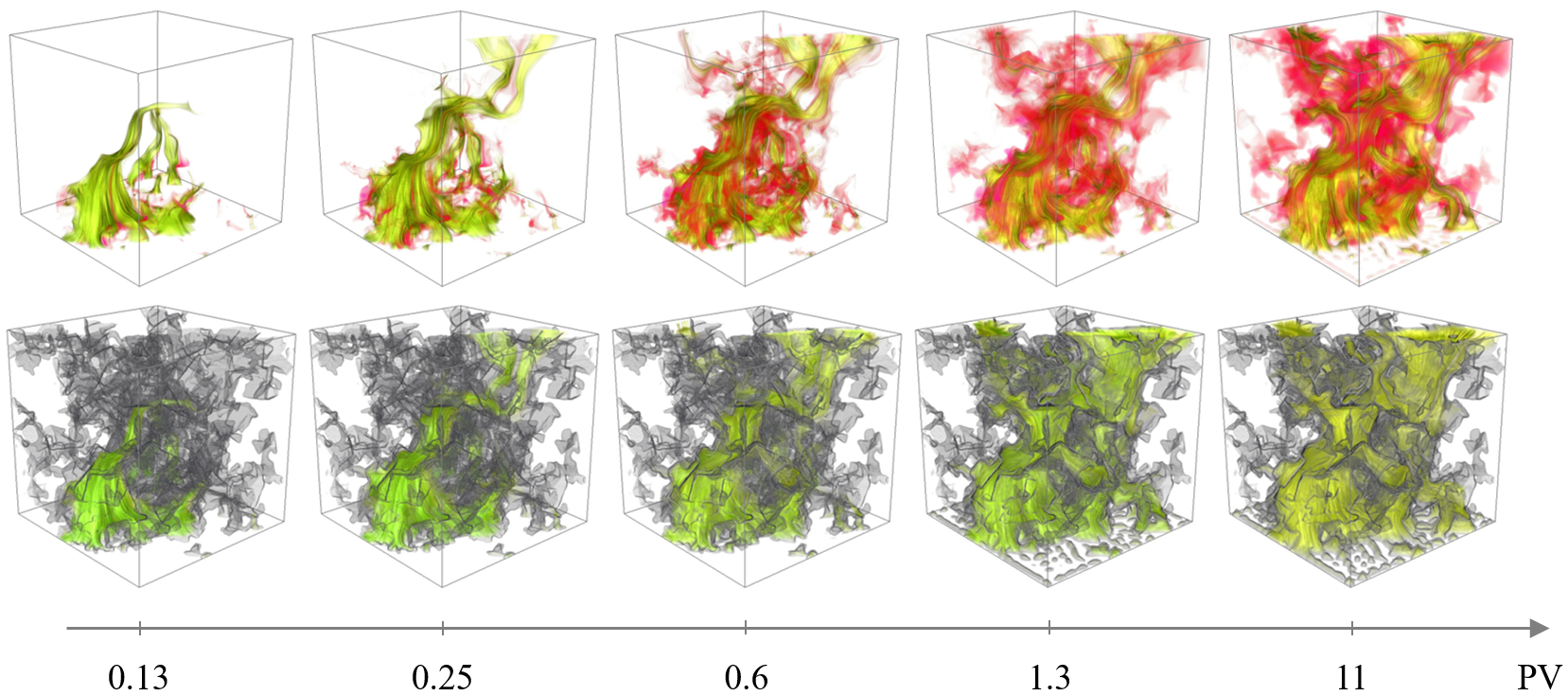
Рис. 3. Распределения кислоты (в желто-зеленых тонах) + продуктов реакции (красно-фиолетовые) (верхний ряд) и поверхности минерала (серая) + кислоты (нижний ряд) после закачки 0,13–11 поровых объемов раствора кислоты на высокой скорости (перепад давления 1750 Бар/м).
Из-за достаточно низкой скорости реакции соляной кислоты и доломита, и короткой продолжительности моделируемого процесса, изменения поровой структуры (серый цвет в нижнем ряду на рис. 3) слабо заметны. В конце обработки прирост пористости модели составил всего 5,5% (с 20,1% до 25,6%), в то время как проницаемость стала в 4,5 раза выше исходной (рис. 4).
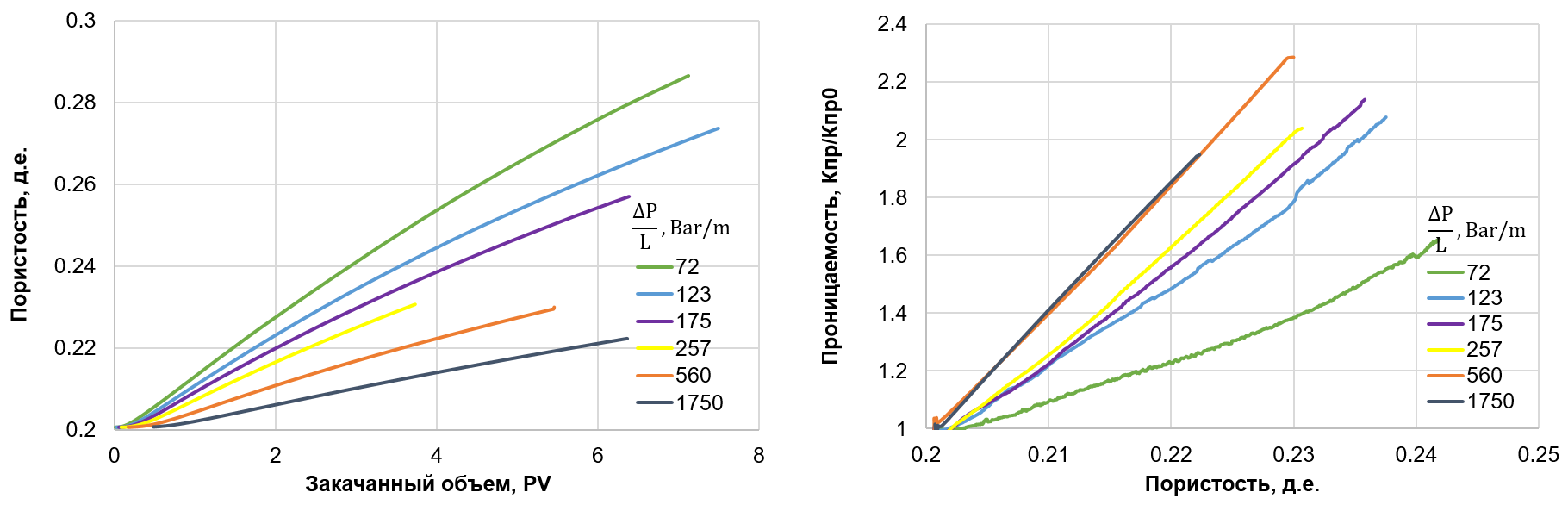
Рис. 4. Зависимость пористости модели от объема закаченного раствора кислоты (слева) и зависимость мгновенной проницаемости от пористости (справа) при различных перепадах давления закачки.
В процессе прокачки реакционного флюида происходит растворение породы на поверхности, контактирующей с раствором кислоты, что приводит к постепенному изменению геометрии порового пространства. Неоднородность распределения активного компонента раствора, обусловленная гетерогенной химической реакцией, диффузионным транспортом и массопереносом в условиях ограниченного порового пространства, может приводить к неравномерному растворению минеральной матрицы. Это выражается в зависимости ключевых параметров процесса, таких как скорость растворения, изменение пористости и проницаемости, от скорости потока реакционного флюида.
В ходе серии численных экспериментов были определены эффективные параметры реакции в пористой среде. Моделирование проводилось при различных перепадах давления в диапазоне от 72 до 1750 Бар/м. По результатам расчетов оценивались количество растворенного минерала и прирост пористости, средняя скорость течения (скорость фильтрации) и скорость растворения минерала – общая скорость эффективной реакции в объеме. После чего, по известным давлению, скорости течения и вязкости флюида определялась эффективная мгновенная проницаемость модели (рис. 4–7).
Анализ зависимостей пористости и проницаемости (рис. 4) демонстрирует сложность формулировки универсального критерия эффективности растворения. С точки зрения затрат кислоты на единицу прироста пористости наиболее эффективным является режим закачки при минимальном давлении. В этом случае большая часть кислоты расходуется на растворение минерального скелета и не проникает в породу на расстояние, превышающее длину модели. Однако скорость роста проницаемости в зависимости от пористости достигает верхнего предела при перепаде давления 560 Бар/м и не увеличивается при дальнейшем повышении давления. Очевидно, что при таких условиях реализуется мгновенное, по сравнению с другими процессами, обновление концентрации кислоты в каналах, и условия протекания реакции оказываются одинаковыми во всех частях модели.
Примечательно, что уже одна эта особенность порождает немонотонность в поведении системы. Если рассматривать эффективность роста проницаемости на единицу затраченной кислоты (рис. 5), видно, что наибольший эффект проявляется при средних значениях перепада давления, тогда как минимальный и максимальный перепады обеспечивают вдвое меньшую эффективность. В терминах затрат раствора, необходимых для достижения заданного прироста проницаемости, наблюдаемый эффект описывается немонотонной функцией от перепада давления (рис. 5, справа).
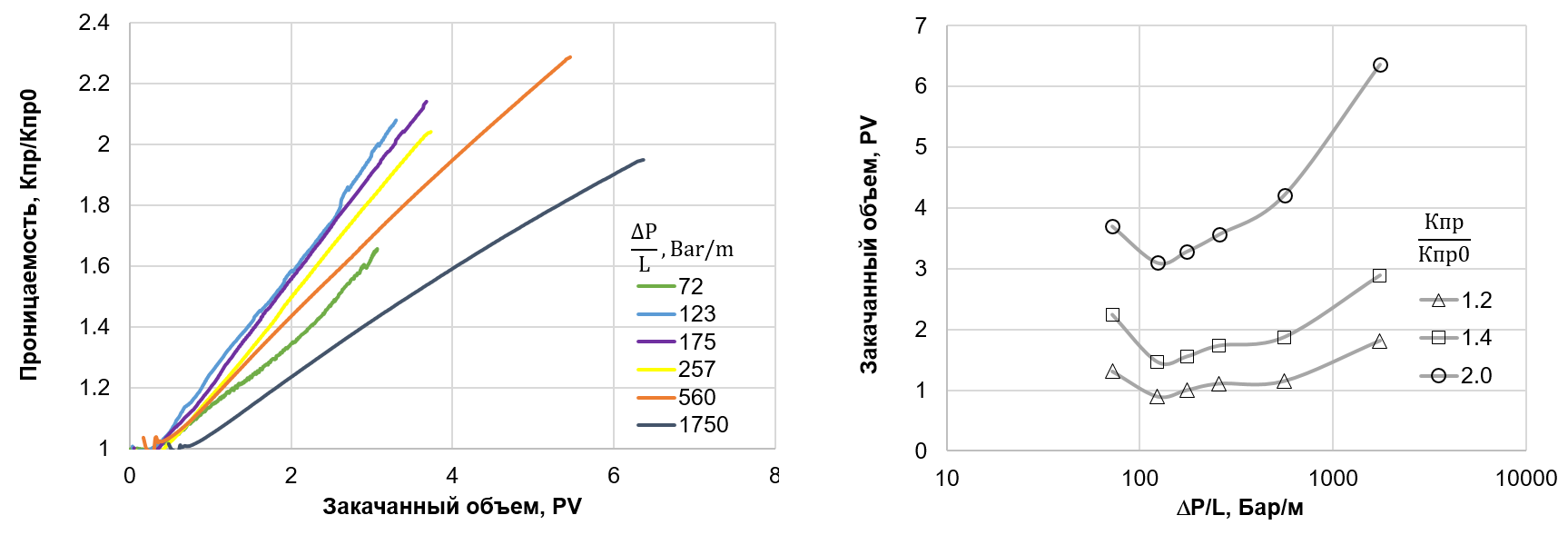
Рис. 5. Проницаемость как функция закачанного объема кислоты при различных перепадах давления закачки (слева). Зависимость объема кислоты, необходимого для достижения заданного прироста проницаемости, от перепада давления.
Поскольку моделирование проводилось при постоянном перепаде давления, наблюдался рост скорости потока флюида, связанный с изменением проницаемости модели со временем. На рис. 6 представлены зависимости скорости растворения минерала от изменяющейся в ходе закачки скорости фильтрации. Моменты, соответствующие закачке одного порового объема модели, отмечены стрелками и выделены цветом. Скорость растворения, в отличие от скорости химической реакции, отражает общую скорость убыли минеральной фазы в системе и учитывает процессы адвекции, диффузии, кинетику реакции и изменение площади поверхности пор. Видно, что основной рост скорости растворения происходит на начальном этапе моделирования, когда при практически неизменной скорости прокачки происходит замещение в модели фонового флюида раствором кислоты. Дальнейшее увеличение скорости растворения происходит одновременно со значительным увеличением проницаемости и скорости течения. При этом участки, соответствующие увеличению скорости течения, во всех рассмотренных случаях описываются единой степенной функцией. На микроуровне этот рост обусловлен интенсификацией транспорта активных компонентов флюида к зоне реакции на поверхности пор.
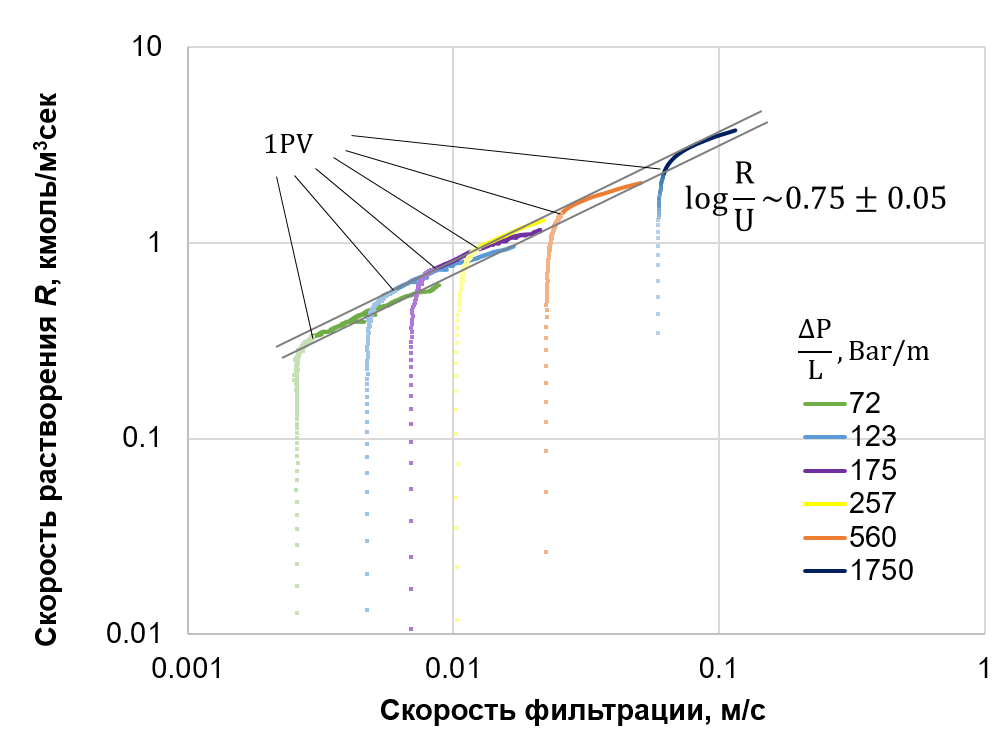
Рис. 6. Динамика скорости растворения минерала от скорости фильтрации при различных перепадах давления закачки раствора. Стрелками указаны точки, соответствующие закачке 1 PV, также значениям до этого момента соответствуют более светлые оттенки. Огибающая (пара серых линий) соответствует функции R ∞ Uq, q ~ 0.75 ± 0.05.
Как уже отмечалось, скорость потока оказывает значительное влияние на эффективную скорость реакции, изменение пористости и, как следствие, на динамику проницаемости. Предположительно, все четыре параметра (скорость потока, эффективная скорость реакции, пористость и проницаемость) взаимосвязаны. Однако количества проведенных численных экспериментов недостаточно для однозначного определения всех параметров модели и установления количественных зависимостей между ними.
Для изучения влияния скорости адвекции на скорость растворения минерала рассмотрим дополнительный параметр – первое число Дамкелера (Da1), которое характеризует скорость изменения концентраций вследствие протекания реакции и имеет размерность обратного времени релаксации. Этот параметр выражается через известную скорость эффективной реакции (R) и концентрацию активного компонента раствора в порах (Ca): Da1 = R/ Ca. В отсутствие ограничений, связанных с конечной скоростью транспорта, характерный временной масштаб Da1 определяется исключительно кинетикой процесса, то есть коэффициентом скорости реакции и коэффициентами активности. Однако в условиях потока в гетерогенной среде значение этого параметра лимитируется более медленными процессами, особенно при низких скоростях течения (рис. 7, линии 72 и 123 Бар/м).
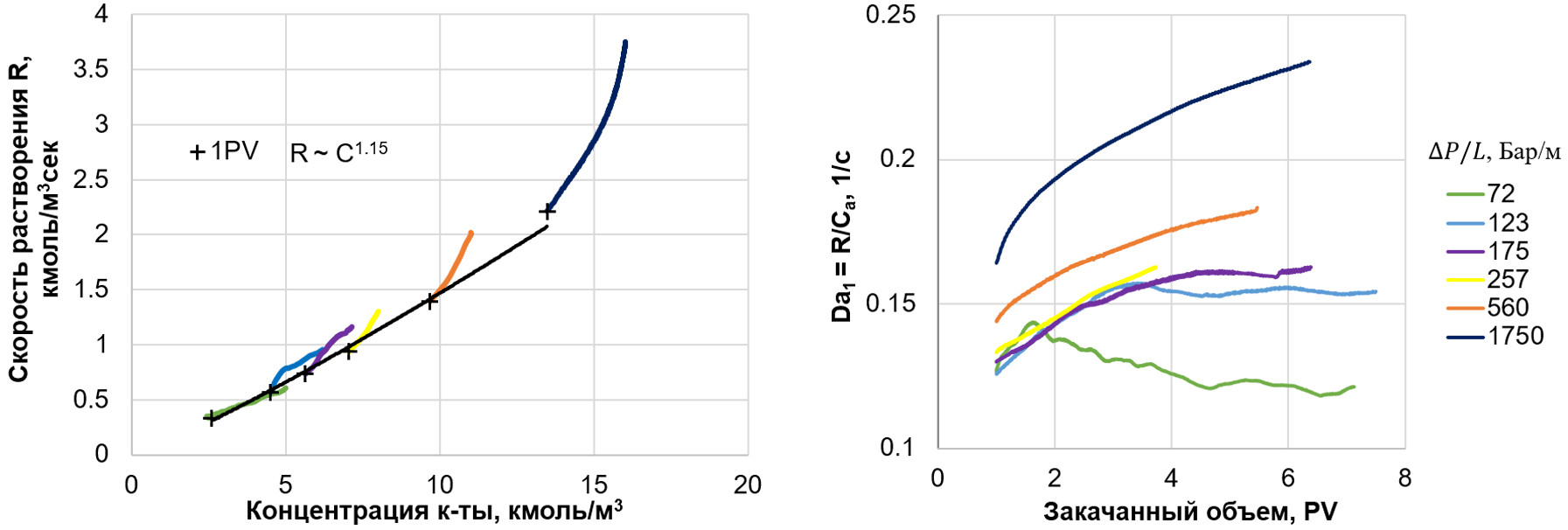
Рис. 7. Скорость растворения породы (R) в зависимости от концентрации активного компонента кислоты (слева) и характерная скорость релаксации (Da1) как функция закачанного объема кислотного раствора (справа) при различных перепадах давления закачки. Показана динамика после закачки 1 PV. Огибающая проведена через точки, соответствующие закачке 1 PV.
Этот эффект хорошо иллюстрируется расчетами, показывающими, что при низких скоростях закачки процесс растворения контролируется не кинетикой реакции, а более медленными процессами, такими как диффузионный перенос. На графике зависимости Da1 от объема закачанной кислоты (рис. 7, справа) видно, что с увеличением скорости закачки перемешивание становится более интенсивным, и влияние структуры порового пространства проявляется позже или не проявляется вовсе. При низких скоростях это влияние выражается в отклонении скорости релаксации (Da1) от монотонного тренда, что подчеркивает роль диффузии и структуры пор в управлении процессом растворения.
Рассмотренные характеристики и взаимосвязи между ними описывают эффективное поведение модели на масштабе, превышающем размер пор, при изменениях, вызванных течением реакционного раствора. Полученные результаты могут быть использованы на моделях большего масштаба. Например, связь изменений пористости и проницаемости – для вывода замыкающих соотношений для уравнений фильтрации (Дарси) в среде с меняющейся со временем (в силу химических реакций) пористостью и проницаемостью; а зависимость скорости растворения минерала от скорости потока – для определения поправки в кинетический закон эффективной реакции. Для этого может быть необходимо проведение подобных расчетов на наборе поровых моделей с различными исходными пористостью, проницаемостью и структурой пор и последующее построение модели образца с учетом внутренней неоднородности транспортных свойств, как это было сделано в (Ivanov et al., 2023).
Заключение
Проведенное исследование продемонстрировало возможности метода функционала плотности для гидродинамики (DFH) в моделировании кислотной обработки карбонатных коллекторов на поровом уровне. При моделировании учитывалась гетерогенность структуры порового пространства, а также кинетика химических реакций и гидродинамических процессов. Были определены ключевые закономерности, влияющие на эффективность растворения минеральной матрицы потоком раствора кислоты.
Получены зависимости пористости и проницаемости от перепада давления закачки и объема закачанного кислотного раствора. Продемонстрировано влияние скорости закачки на равномерность и эффективность растворения породы. Определена оптимальная с точки зрения затрат кислотного раствора скорость закачки и установлена асимптотическая зависимость скорости растворения от скорости закачки.
Предложенный подход позволяет корректно описывать связь химических и гидродинамических процессов на микроуровне. Полученные результаты имеют практическое значение для решения задач по интенсификации добычи, включая выбор оптимальных скоростей закачки и состава кислотных растворов. Возможность получения эффективных зависимостей, описывающих поведение породы при взаимодействии с кислотным раствором, на масштабе уравнения Дарси открывает перспективу получения входных данных для моделей и симуляторов большего масштаба с учетом как особенностей химического состава кислот, так и специфики структуры обрабатываемых пород, что дает возможность существенно повысить точность моделирования и качество кислотных обработок.
В дальнейшем планируется направить исследования на расширение модели для учета многофазных течений, термодинамических эффектов и гетерогенного состава минеральной матрицы.
Список литературы
1. Ali M.T., Nasr-El-Din H.A. (2020). New insights into Carbonate Matrix Acidizing Treatments: A Mathematical and Experimental Study. SPE Journal. SPE-200472-PA. https://doi.org/10.2118/200472-PA
2. Beletskaya A., Ivanov E., Stukan M., Safonov S., Dinariev O. (2017). Reactive Flow Modeling at Pore Scale. Presented at the SPE Russian Petroleum Technology Conference, 16–18 October, Moscow, Russia. SPE187805-RU. https://doi.org/10.2118/187805-MS
3. Busenberg E., Plummer L.N. (1982). The Kinetics of Dissolution of Dolomite in CO2 – H2O System 1.5 to 65 ºC and 0 to 1 atm PCO2. Am. J. Sci., 282(1), pp. 45–78. https://doi.org/10.2475/ajs.282.1.45
4. Chung T.J. (2002). Computational Fluid Dynamics. Cambridge: Cambridge University Press.
5. Demianov A., Dinariev O., Evseev N. (2011). Density Functional Modelling in Multiphase Compositional Hydrodynamics. Can. J. Chem. Eng., 89(2), pp. 206–226. https://doi.org/10.1002/cjce.20457
6. Demianov A.Yu., Dinariev O.Yu., Evseev N.V. (2014). Introduction to The Density Functional Method in Hydrodynamics. Moscow: Fizmatlit.
7. Dubetz D., Cheng H., Zhu D., Hill A.D. (2016). Characterization of Rock Pore-Size Distribution and its Effects on Wormhole Propagation. Presented at the SPE Annual Technical Conference and Exhibition, Dubai, 26–28 September. SPE-181725-MS. https://doi.org/10.2118/181725-MS
8. Etten J., Zhu D., Hill A.D. (2015). The Combined Effect of Permeability and Pore Structure on Carbonate Matrix Acidizing. Presented at the EUROPEC 2015, Madrid, 1–4 June. SPE-174314-MS. https://doi.org/10.2118/174314-MS
9. Gautelier M., Oelkers E.H., Schott J. (1999). An Experimental Study of Dolomite Dissolution Rates as a Function of pH from −0.5 to 5 and Temperature from 25 to 80°C. Chemical Geology, 157(1–2), pp. 13–26. DOI: 10.1016/S0009-2541(98)00193-4
10. Gingold R.A., Monaghan J.J. (1977). Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars. Mon Not R Astron Soc., 181, pp. 375–389. https://doi.org/10.1093/mnras/181.3.375
11. Glasbergen G., Kalia N., Talbot M.S. (2009). The Optimum Injection Rate for Wormhole Propagation: Myth or Reality? Presented at the 8th European Formation Damage Conference, Scheveningen, 27–29 May. SPE-121464-Ms. https://doi.org/10.2118/121464-MS
12. Ivanov E., Evseev N., Dinariev O. (2014). Rheological Effects in Twophase Microflow. Proc. International Conference on Heat Transfer and Fluid Flow, Prague, Czech Republic, August 11–12. Paper No. 64.
13. Ivanov E. et al, (2020). Acid Treatment Optimization based on Digital Core Analysis. Presented at the SPE Russian Petroleum Technology Conference, 12–14 October, Moscow, Russia. SPE-202016.
14. Ivanov E. et al, (2023). Digital Core Analysis as an Efficient Tool for Acid Treatment Optimization. Presented at the 2021 International Symposium of the Society of Core Analysts. E3S Web of Conferences 366, 01002 (2023), DOI: 10.1051/e3sconf/202336601002
15. Kim, D., Lindquist, W. B. 2012. Dependence of Pore-to-Core Up-scaled Reaction Rate on Flow Rate in Porous Media. Transp Porous Med., 94(2), pp. 555–569. https://doi.org/10.1007/s11242-012-0014-0
16. Klemin D., Nadeev A., Ziauddin M. (2015). Digital Rock Technology for Quantitative Prediction of Acid Stimulation Efficiency in Carbonates. Presented at the SPE Annual Technical Conference and Exhibition, Houston, Texas, USA, 28–30 September. SPE-174807-MS. https://doi.org/10.2118/174807-MS
17. Lisitsa V., Bazaikin Y., Khachkova T. (2020). Computational topologybased characterization of pore space changes due to chemical dissolution of rocks, Applied Mathematical Modelling, 88, pp. 21–37.
18. Qiu X., Aidagulov G., Ghommem M., Edelman E., Brady D., Abbad M. (2018). Towards a better understanding of wormhole propagation in carbonate rocks: Linear vs. radial acid injection. Journal of Petroleum Science and Engineering, 171, pp. 570–583. https://doi.org/10.1016/j.petrol.2018.07.075
19. Sevougian S.D., Lake L.W., Schechter R.S. (1995). A New Geochemical Simulator to Design More Effective Sandstone Acidizing Treatments. SPE Production & Facilities, 10(01), pp. 13–19. SPE-24780-PA. https://doi.org/10.2118/24780-PA
20. Steefel C.I., Appelo C.A.J., Arora B., Jacques D., Kalbacher T., Kolditz O., Lagneau V., Lichtner P.C., Mayer K.U., Meeussen J.C.L., Molins S., Moulton D., Shao H., Šimůnek J., Spycher N., Yabusaki S.B., Yeh G.T. (2015). Reactive transport codes for subsurface environmental simulation. Computat Geosci., 19(3), pp. 445–478. https://doi.org/10.1007/s10596-014-9443-x
21. Wolf-Gladrow D.A. (2000). Lattice-Gas Cellular Automata and LatticeBoltzmann Models. Berlin: Springer.
22. Ziauddin M.E., Bize E. (2007). The Effect of Pore Scale Heterogeneities on Carbonate Stimulation Treatments. Presented at the SPE Middle East Oil and Gas Show and Conference, Manama,11–14 March. SPE-104627-MS. https://doi.org/10.2118/104627-MS
23. Ziauddin M., Robert J. (2003). Method of optimizing the design, stimulation and evaluation of matrix treatment in a reservoir. US Patent US006668922B2.
Об авторах
Е. Н. ИвановРоссия
Евгений Николаевич Иванов – кандидат физ.-мат. наук,
старший научный сотрудник
125171, Москва, Ленинградское ш., 16А, стр. 3
Д. А. Коробков
Россия
Дмитрий Александрович Коробков – кандидат тех.
наук, старший научный сотрудник
125171, Москва, Ленинградское ш., 16А, стр. 3
М. Р. Стукан
Россия
Михаил Реональдович Стукан – кандидат физ.-мат.
наук, начальник исследовательского отдела
125171, Москва, Ленинградское ш., 16А, стр. 3
Рецензия
Для цитирования:
Иванов Е.Н., Коробков Д.А., Стукан М.Р. Влияние параметров течения реакционного флюида на скорость растворения породы коллектора. Георесурсы. 2025;27(2):206–215. https://doi.org/10.18599/grs.2025.2.16
For citation:
Ivanov E.N., Korobkov D.A., Stukan M.R. Influence of the Reactive Fluid Flow Regime on Mineral Dissolution Rate. Georesursy = Georesources. 2025;27(2):206–215. (In Russ.) https://doi.org/10.18599/grs.2025.2.16
JATS XML















.png)


