Перейти к:
Особенности реконструкции современных напряжений в карбонатных породах на примере нефтяного месторождения Республики Татарстан
https://doi.org/10.18599/grs.2025.1.11
Аннотация
В работе приводятся результаты лабораторных исследований физико-механических свойств керна карбонатных пород на одном из нефтяных месторождений Республики Татарстан. Полученные экспериментальные данные совместно с результатами геофизических исследований скважин и данных о гидроразрыве пласта были использованы для расчета напряженно-деформированного состояния массива горных пород. Вычисление величин горизонтальных напряжений выполнено с применением пороупругой модели Итона, в которой предварительно были определены коэффициенты деформации на глубине проведения гидроразрыва породы. Минимальное горизонтальное напряжение было определено как давление смыкания трещины гидроразрыва, а максимальное горизонтальное напряжение вычислено по диаграмме напряжений (совмещение критерия разрушения породы и классификации тектонических режимов). При реконструкции напряжений использовались упругие модули, полученные по лабораторным исследованиям. В результате вычислены величины основных главных напряжений вдоль разреза скважины, и определен тектонический режим, действующий на данном месторождении. Получены уравнения зависимости для прочностных свойств пород, слагающих разрез, и вычислены значения прочности вдоль всего ствола скважины. На базе полученной геомеханической модели рассчитана зависимость давления гидроразрыва от длины трещины и оценены условия неконтролируемого роста трещины.
Ключевые слова
Для цитирования:
Зиганшин Э.Р., Косарев В.Е., Фаттахов А.В., Гильфанов С.И., Скоробогатова М.А., Маликов А.Д., Сергеев А.С. Особенности реконструкции современных напряжений в карбонатных породах на примере нефтяного месторождения Республики Татарстан. Георесурсы. 2025;27(1):135-143. https://doi.org/10.18599/grs.2025.1.11
For citation:
Ziganshin E.R., Kosarev V.E., Fattakhov A.V., Gilfanov S.I., Skorobogatova M.A., Malikov A.D., Sergeev A.S. Features of Stress State Reconstruction in Carbonate Rocks on the Example of an Oil Field of the Republic of Tatarstan. Georesursy = Georesources. 2025;27(1):135-143. (In Russ.) https://doi.org/10.18599/grs.2025.1.11
Введение
Существует ряд задач, связанных с разработкой месторождений, которые довольно успешно решаются при помощи нефтегазовой геомеханики – раздела науки о напряженном состоянии массива горных пород и его физико-механических свойствах на нефтегазовых месторождениях (Plumb et al., 2000). К таким задачам относятся: безаварийное бурение скважины, проведение операции по гидроразрыву пород, выявление зон с аномально высоким пластовым давлением, оценка флюидопроводимости разломов и трещин, утилизация углекислого газа (Afsari et al., 2009; Ismail et al., 2020; Jimenez et al., 2005; Zain-Ulabedin et al., 2020). Основным решением вышеперечисленных задач является построение геомеханической модели. В общем понимании, геомеханическая модель базируется на двух «блоках». Первый «блок» – это величина и направление основных главных напряжений и порового давления, второй – физико-механические свойства горных пород, которые слагают изучаемый объект. Корректные данные о механических свойствах пород можно получить только при помощи прямых лабораторных измерений. Ни одна из геомеханических моделей не может быть корректно построена без лабораторных исследований керна. Результаты экспериментов позволяют оценить упруго-прочностные свойства пород, слагающих изучаемый объект, а также участвуют в оценке напряженно-деформированного состояния горных пород.
Существует ряд методов для определения величины и направления главных напряжений в массивах горных пород, которые слагают нефтяные и газовые месторождения (Ljunggren et al., 2003; Дубиня, 2019). Одним из наиболее популярных методов является анализ вывалов и техногенных трещин, вызванных бурением, на стенках вертикальных скважин. Однако данный метод осуществим только при наличии специальных геофизических исследований (сканирование стенок скважин электрическими и акустическими микроимиджерами), объем которых ограничен. К тому же, если на месторождении не наблюдается сильного контраста величин основных главных напряжений, то вывалы и трещины могут не образоваться.
Одним из наиболее достоверных методов определения величины минимального главного напряжения является метод оценки по результатам гидроразрыва пласта (ГРП) или мини-гидроразрыва пласта (Gaarenstroom et al., 1993). В этом случае минимальное главное напряжение будет равно давлению закрытия трещины гидроразрыва. Это точечное исследование, которое дает величину только непосредственно на глубине проведения ГРП. Существует ряд исследований, где допускается, что отношение вертикального напряжения к минимальному горизонтальному напряжению одинаково для всего разреза скважины. Используя данное допущение, вычисляется непрерывный профиль минимального напряжения. Однако опыт показывает, что величина минимального горизонтального напряжения может меняться с глубиной неравномерно, в зависимости от типа породы.
В настоящей работе показан алгоритм определения величины главных напряжений и физико-механических свойств пород, основанный на комплексировании лабораторных геомеханических исследований керна и специальных исследованиях скважин. Профиль напряжений рассчитывался с применением пороупругой модели (Prats, 1981), которая была откалибрована по результатам мини-ГРП и по диаграмме напряжений. Благодаря полученным эмпирическим уравнениям построены профили упруго-прочностных свойств горных пород вдоль всего изучаемого разреза.
Материалы и методы
Объектом исследования в настоящей работе является нефтяное месторождение, сложенное карбонатными породами. Месторождение располагается на территории Республики Татарстан, в западной части Южно-Татарского свода (Хисамов и др., 2006) (рис. 1). Разрез представлен комплексом осадочных пород каменноугольного, пермского и четвертичного возрастов. Нефтепродуктивными являются известняки верейских и башкирско-серпуховских отложений среднего карбона. Породы башкирского яруса сложены плотными известняками. В этом интервале наблюдается наличие естественной трещиноватости. Породы верейского горизонта условно можно разделить на терригенные и карбонатные (Муслимов и др., 2007).
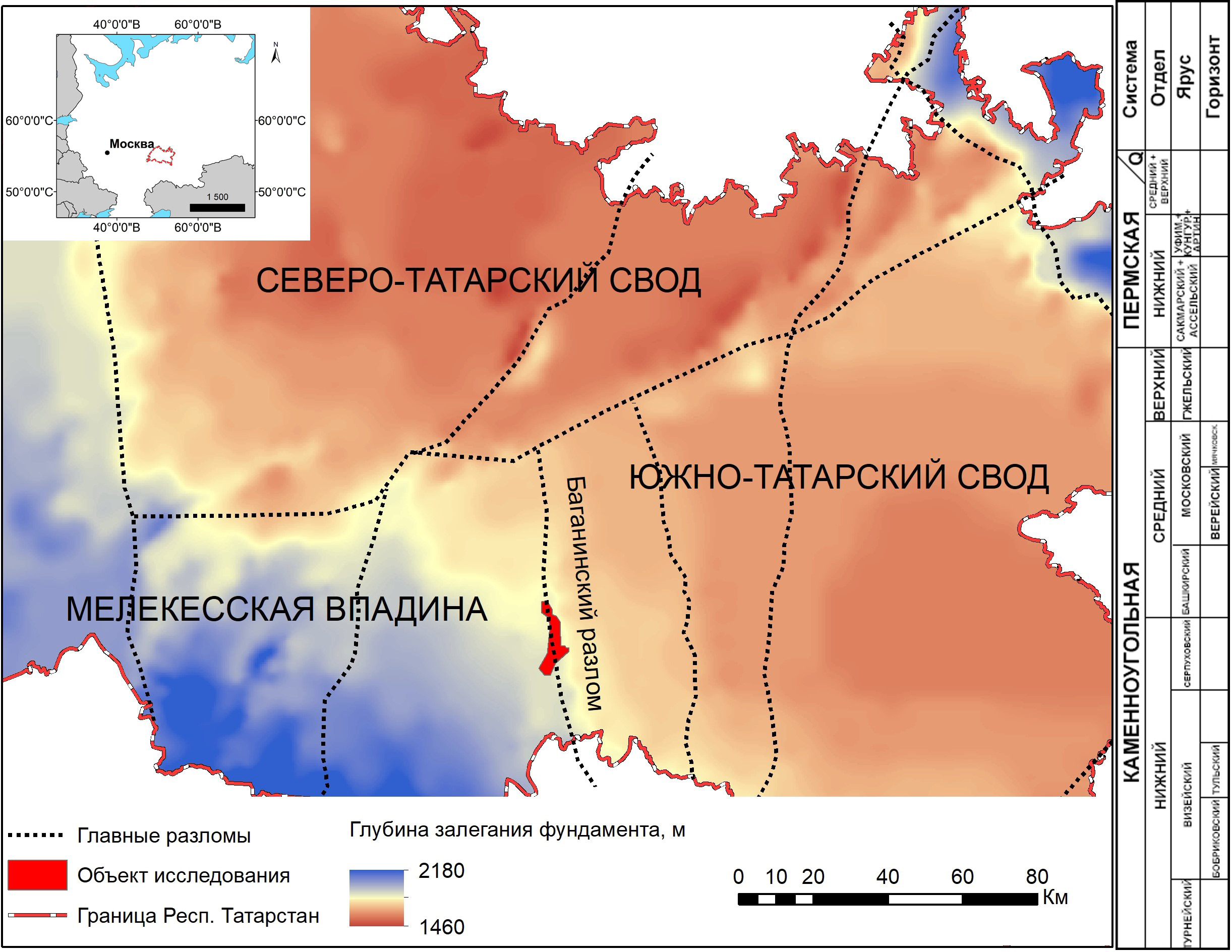
Рис. 1. Объект исследования, стратиграфический разрез, вскрытый скважиной
Керновый материал был отобран в интервале глубин 892,5–980,5 м. Интервал представлен породами среднекаменноугольного возраста: башкирский ярус, верейский и каширский горизонты московского яруса. Всего было отобрано 30 образцов керна: 11 образцов из каширского горизонта, 16 образцов из верейского горизонта и 3 образца из башкирского яруса (рис. 2).

Рис. 2. Фото керна для исследований (верейский горизонт)
Комплекс лабораторных геомеханических исследований включал в себя определение динамических упругих параметров и статических упруго-прочностных характеристик. Определение упругих, деформационных и прочностных свойств в условиях трехосного сжатия выполнялось согласно требованиям (Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures ASTM D7012-14, 2014). Испытания проводились в состоянии естественного насыщения при эффективном давлении 5, 10, 15, 20 МПа для трехосных испытаний. Измерение упругих и прочностных свойств осуществлялось в камере трехосного осесимметричного сжатия при помощи осевых и радиальных датчиков линейного перемещения (рис. 3).

Рис. 3. Установка для испытания керна ГТЯН (НПП «Геотек», Россия)
По кривым напряжения-деформации фиксировалась пиковая нагрузка, на которой происходило разрушение образца, что соответствует пределу прочности на сжатие. Упругие модули (модуль Юнга, коэффициент Пуассона) определялись по кривым напряжение-деформация в интервале 25–50% от предела прочности согласно методике (Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures ASTM D7012-14, 2014) (рис. 4).
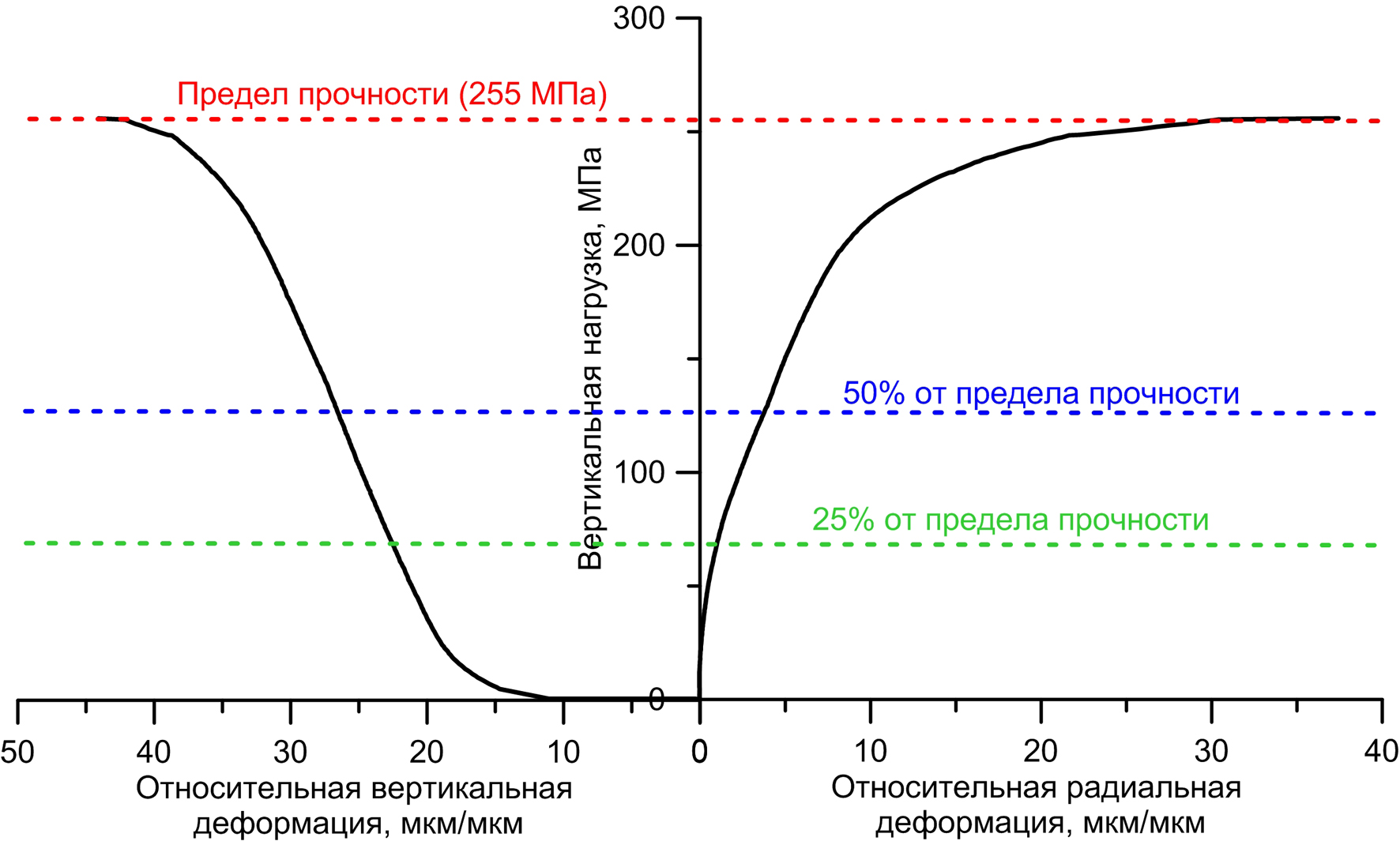
Рис. 4. Пример графиков «напряжение-деформация»
Определение предела прочности на растяжение при раскалывании методом приложения сжимающей нагрузки вдоль диаметра образца в форме диска выполнялось согласно требованиям (Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens ASTM D3967-08, 2008). Испытания проводились на образцах в форме диска с отношением толщины к диаметру (t/D) от 0,2 до 0,75. Дискообразный образец помещался в приспособление одноосного растяжения установки ГТЯН.441179.050 и зажимался в радиальном направлении. Нагрузка увеличивалась с заданной скоростью деформации до разрушения образца (например, 0,1 МПа/с). Предел прочности на разрыв определялся из предельной нагрузки по методике (Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens ASTM D3967-08, 2008).
Значения коэффициента трещиностойкости KIC определялись на образцах полудисках с диаметром 62 мм. Процедура пробоподготовки образца к испытаниям подробно описана в методике (The ISRM Suggested Methods for Rock Characterization..., 2015).
Результаты
По результатам лабораторных исследований построены графики зависимости между интервальным временем пробега упругой волны и модулем Юнга и пределом прочности на одноосное сжатие (рис. 5).
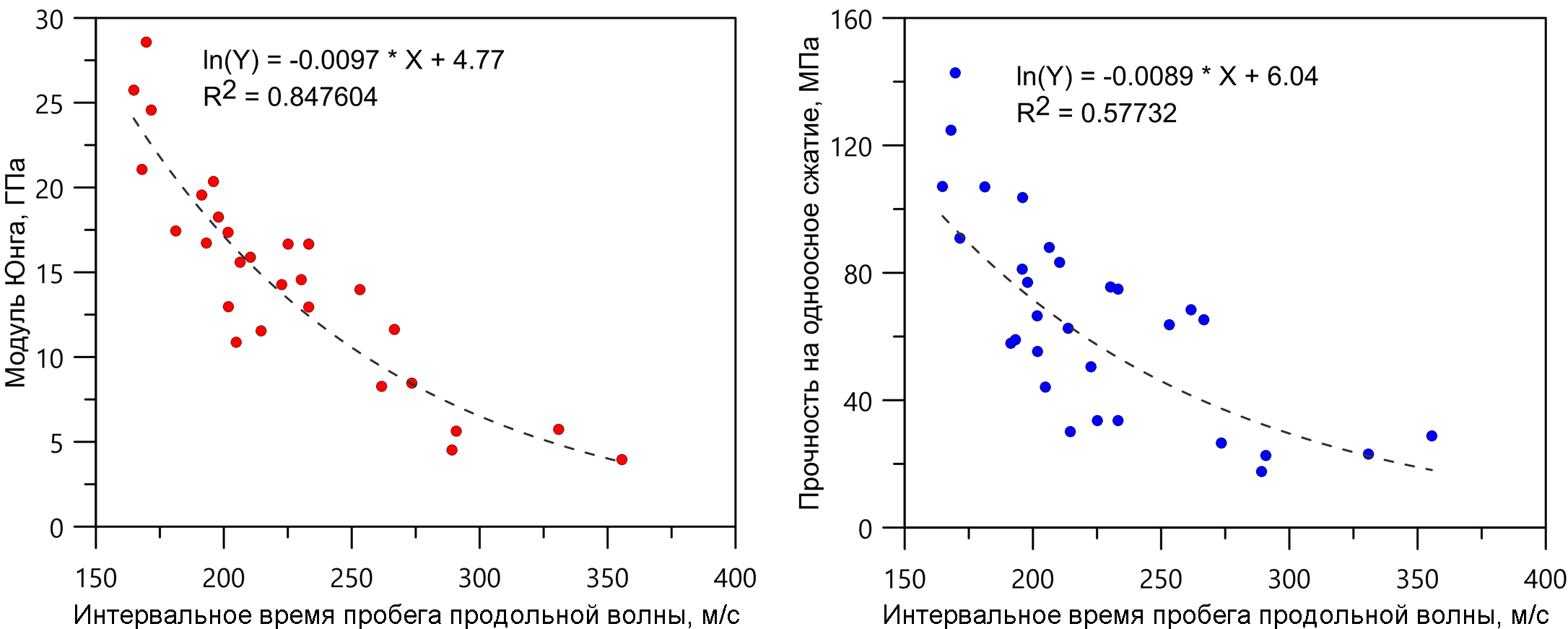
Рис. 5. Графики зависимости между измеренными параметрами керна
Полученные уравнения регрессии позволили использовать результаты акустического каротажа, чтобы вычислить значения упругих и прочностных параметров для всего разреза скважины в виде непрерывных данных с шагом дискретизации 0,1 м.
Коэффициент Пуассона вычислялся с использованием ряда эмпирических уравнений (Khandelwal, Elham, Brocher) и сопоставлялся с результатами лабораторных исследований. Лучшая сходимость с лабораторными исследованиями оказалась у уравнения (Brocher, 2005). Это уравнение было выбрано для вычисления коэффициента Пуассона вдоль всего изучаемого интервала.
Величина вертикального напряжения (Sv) была определена согласно уравнению (1) (Zoback et al., 2003):
![]() , (1)
, (1)
где ρср – это средняя плотность на глубине z, g – ускорение свободного падения.
Для определения величин горизонтальных напряжений, существует ряд методов. Прямым методом определения минимального горизонтального напряжения (Shmin) является тест на утечку или мини-ГРП. В изучаемой скважине был проведен тест на мини-ГРП на глубине 965–967 м. Давление смыкания трещины, равное минимальному горизонтальному напряжению, составляет 13,5 МПа. На этой же глубине значение вертикального напряжения Sv равно 21,5 МПа. Величина SHmax была определена путем построения полигона напряжений (Zoback et al., 2003). Полигон напряжений представляет собой график, отображающий возможные величины горизонтальных напряжений в земной коре для режимов напряжений типа сброс, сдвиг и надвиг, которые ограничены и не могут превышать силы трения существующих разломов. Коэффициент трения по разломам в данном случае был принят равным μ = 0,6 (Zoback et al., 2003). Границы горизонтальных напряжений были определены по критериям Кулона-Мора согласно следующим уравнениям:
Сбросовый режим напряжений
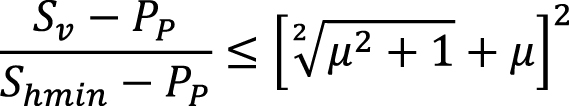 . (2)
. (2)
Сдвиговый режим напряжений
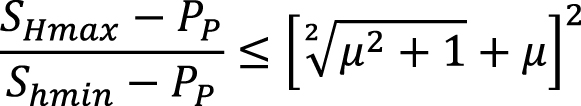 . (3)
. (3)
Надвиговый режим напряжений
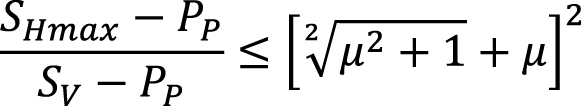 . (4)
. (4)
По результатам построения полигона напряжений получено, что среднее значение SHmax на глубине проведения мини-ГРП равно 15 МПа (рис. 6).
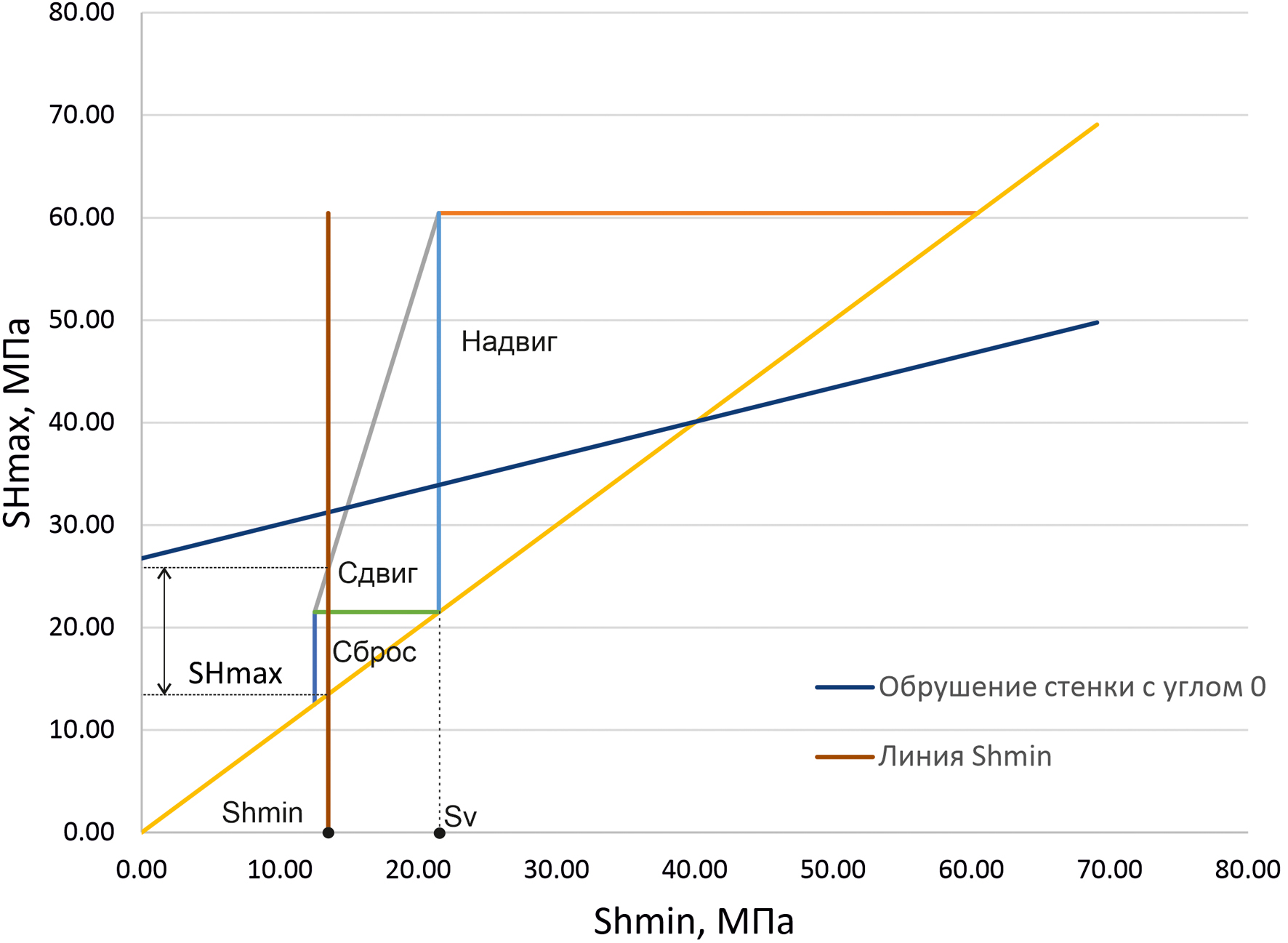
Рис. 6. Полигон напряжений для глубины 965–967 м
Таким образом, на глубине 965–967 м известны три главных напряжения. Следующим шагом является расчет напряжений вдоль всего изучаемого разреза. Для этого была использована пороупругая модель (Zoback et al., 2003), которая описывается уравнениями:
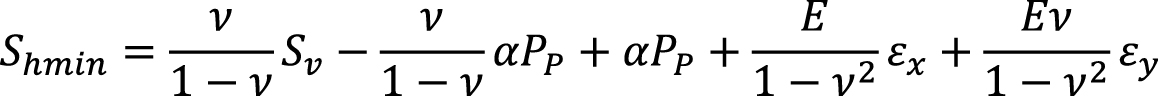 (5)
(5)
![]() (6)
(6)
где εx и εу – относительные деформации в направлении Shmin и SHmax соответственно, зависящие от тектонических сил, действующих в регионе; Pp – поровое давление, МПа; E – статический модуль Юнга, МПа; ν –статический коэффициент Пуассона; α – константа Био.
Модуль Юнга и коэффициент Пуассона были определены при помощи лабораторных геомеханических исследований и рассчитаны для всего разреза скважины благодаря полученным корреляционным зависимостям (рис. 5). Так как глубина исследования является относительно небольшой, то поровое давление можно условно принять как гидростатическое, аналогично уравнению (1), константа Био принята равной 1. основной проблемой является определение εx и εy. Эти константы можно определить на глубине проведения мини-ГРП, где все остальные параметры известны (SHmax, Shmin, Pp, E, ν). Используя уравнения (5) и (6), были определены относительные деформации εx и εy. εx = 0,0167 и εy = 0,0534. если принять допущение, что относительные деформации остаются постоянными для всего разреза, то можно вычислить величины горизонтальных напряжений по всей длине скважины.
На самом деле коэффициенты относительной деформации могут быть непостоянными по всему разрезу. Вероятнее всего, в глинистых интервалах данный коэффициент будет выше, чем в карбонатных породах, где был проведен тест мини-ГРП и определены эти коэффициенты. Для достоверной оценки изменчивости коэффициентов деформации по глубине недостаточно данных, так как прямое измерение Shmin выполнено только в одной точке. В настоящей работе практическое применение результатов реконструкции современных напряжений сводится к оценке рисков роста трещины, следовательно приравнивание коэффициентов деформации в интервале мини-ГРП (карбонатные породы) к вышележащим слоям (в том числе к глинам) делает модель более безопасной. То есть прогнозное давление смыкания трещины в глинах возможно будет немного заниженным, что ещё больше снизит риск развития трещины.
Обсуждение результатов
Таким образом, по результатам лабораторных исследований физико-механических свойств керна совместно с обработкой геофизических данных были получены упруго-прочностные характеристики и величины главных напряжений для всего изучаемого разреза на карбонатном месторождении нефти (рис. 7).
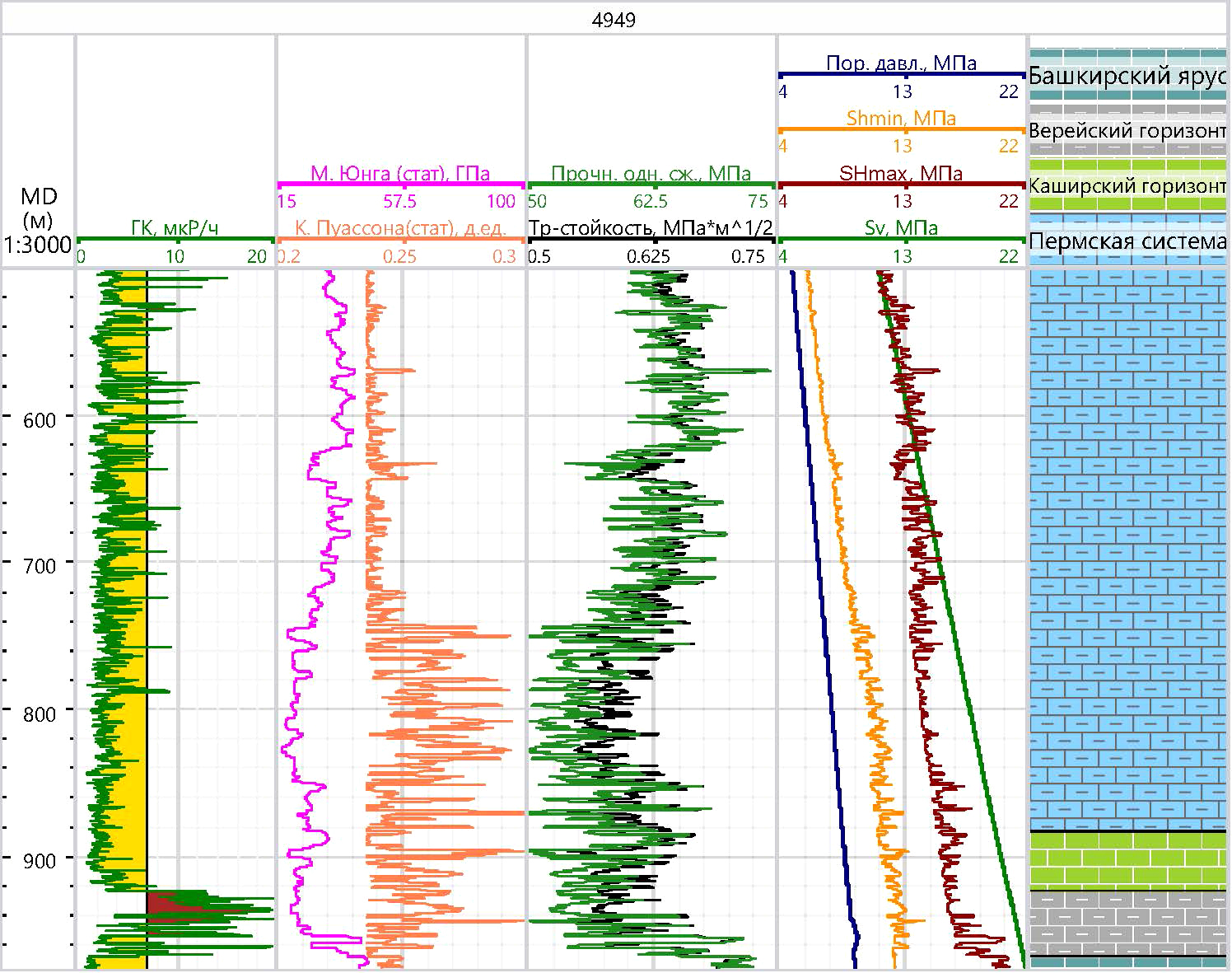
Рис. 7. Геофизический планшет с результатами исследований: модуль Юнга, коэффициент Пуассона, прочность на одноосное сжатие, параметр трещиностойкости, поровое давление и три главных напряжения
В исследуемой скважине практический интерес представляет продуктивный интервал проведения гидроразрыва пласта – башкирские и верейские отложения. Основная трудность, возникающая в процессе ГРП на данном месторождении, вызвана обводнением пласта после проведения гидроразрыва. С точки зрения геомеханических исследований к такому результату могут приводить две основные причины: прорыв трещиной ГРП пород-покрышек до водоносного горизонта или активизация естественной трещиноватости, которая служит проводником для воды. Реконструкция современных напряжений и определение физико-механических свойств пород позволяют оценить вероятность прохождения трещиной ГРП плотных интервалов, представляющих собой «барьеры». Для такой оценки был более подробно рассмотрен интервал проведения гидроразрыва от 915 до 975 м (рис. 8).
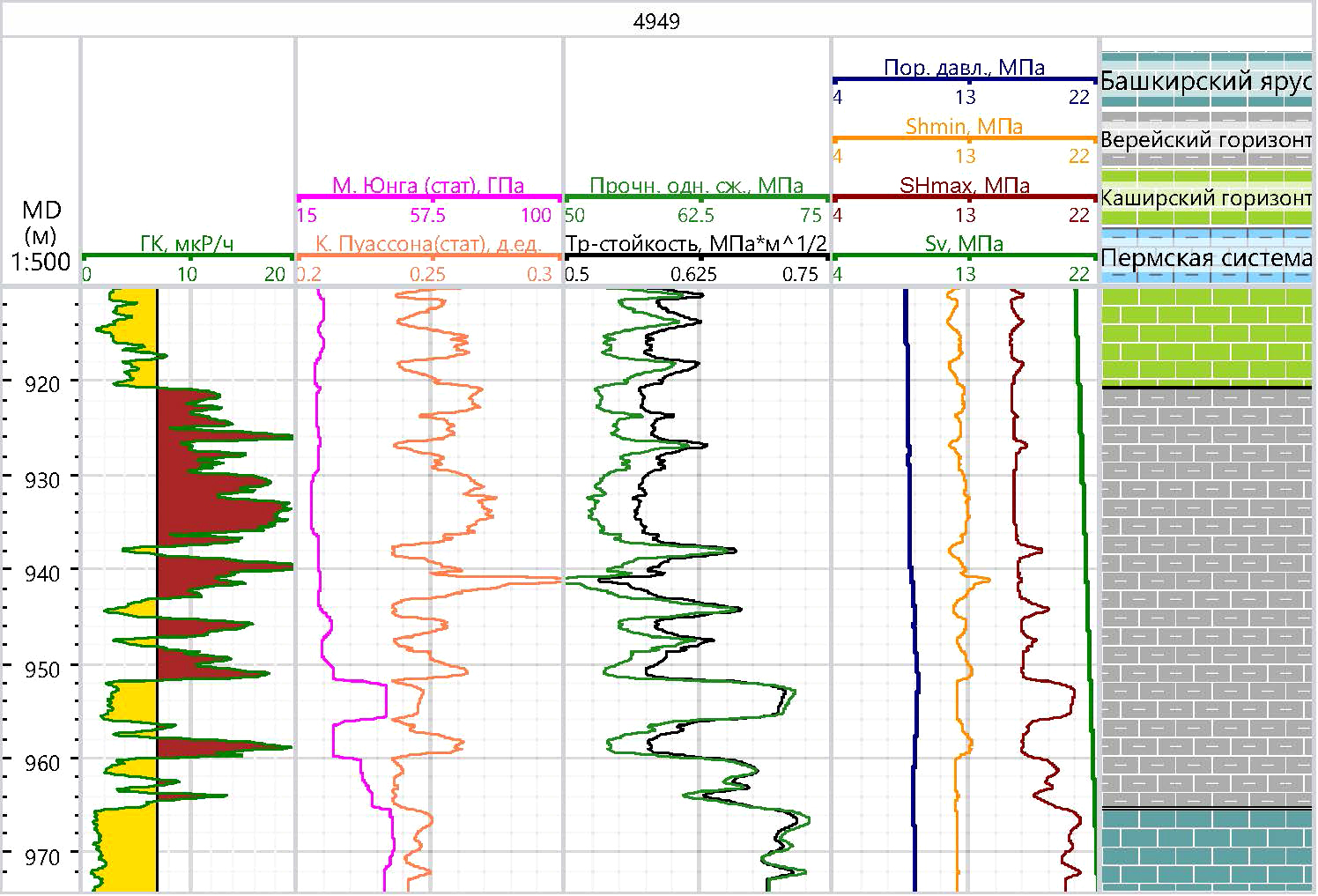
Рис. 8. Геофизический планшет с результатами исследований для интервала 915–975 м
Как было обозначено ранее, давление смыкания трещины в точке ГРП на глубине 965 м составляет 13,5 МПа. Ниже по разрезу величина минимального горизонтального напряжения остается практически неизменной (14 МПа), однако прочность породы увеличивается с 60 до 72 МПа, трещиностойкость увеличивается с 0,63 до 0,71 МПа·м1/2. Выше по разрезу в верейском горизонте встречаются интервалы с пониженной прочностью (до 48 МПа) и трещиностойкостью (до 0,53 МПа·м1/2) и с повышенным минимальным горизонтальным напряжением (до 16 МПа). Изменения величины минимального горизонтального напряжения по глубине, очевидно, во многом обусловлены литологической изменчивостью пород, слагающих разрез. Так, в карбонатной части верейского и башкирского возраста значения Shmin относительно низкие по сравнению с терригенной толщей верейских отложений. В терригенных породах часто встречаются глинистые прослои, которые обладают низкими значениями модуля Юнга и высокими значениями коэффициента Пуассона, что и обуславливает такое распределение напряжений.
Имеющиеся величины напряжений и прочности пород позволяют оценить условия распространения трещины гидроразрыва вверх и вниз по разрезу. В работе (Simonson et al., 1978) решается задача распространения трещины ГРП в слои с отличающимися тектоническими напряжениями. Решение этой задачи описывается уравнением
(7):
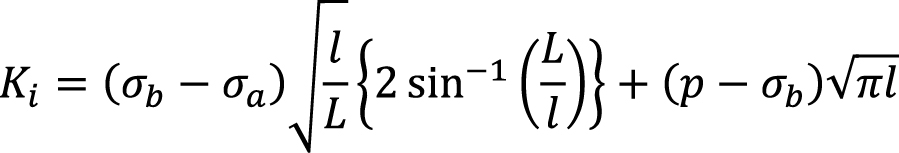 , (7)
, (7)
где Ki – коэффициент интенсивности напряжений, σb, σa – минимальное напряжение в вышележащем пласте и в зоне расположения трещины соответственно, L – полудлина трещины, l – полудлина предполагаемой трещины после её роста, p – давление внутри трещины.
Если принять, что l = L(1 + ε), где ε – это относительное расстояние, пройденное трещиной в область с более высокими напряжениями, то получаем:
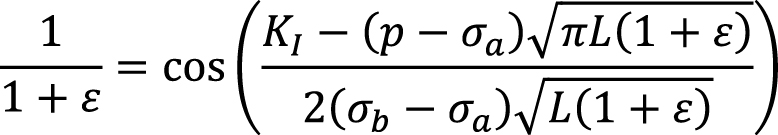 . (8)
. (8)
Допуская, что p0 – это давление, необходимое для роста трещины при ε = 0, то
![]() . (9)
. (9)
Объединив уравнения 8 и 9, получаем:
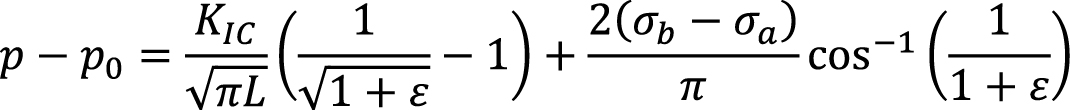 (10)
(10)
Уравнение (10) было использовано для построения модели роста трещины вверх и вниз по разрезу с учетом вычисленных напряжений и механических свойств пород. На рисунке 9 схематично изображен разрез и входные параметры, используемые в уравнении (10).
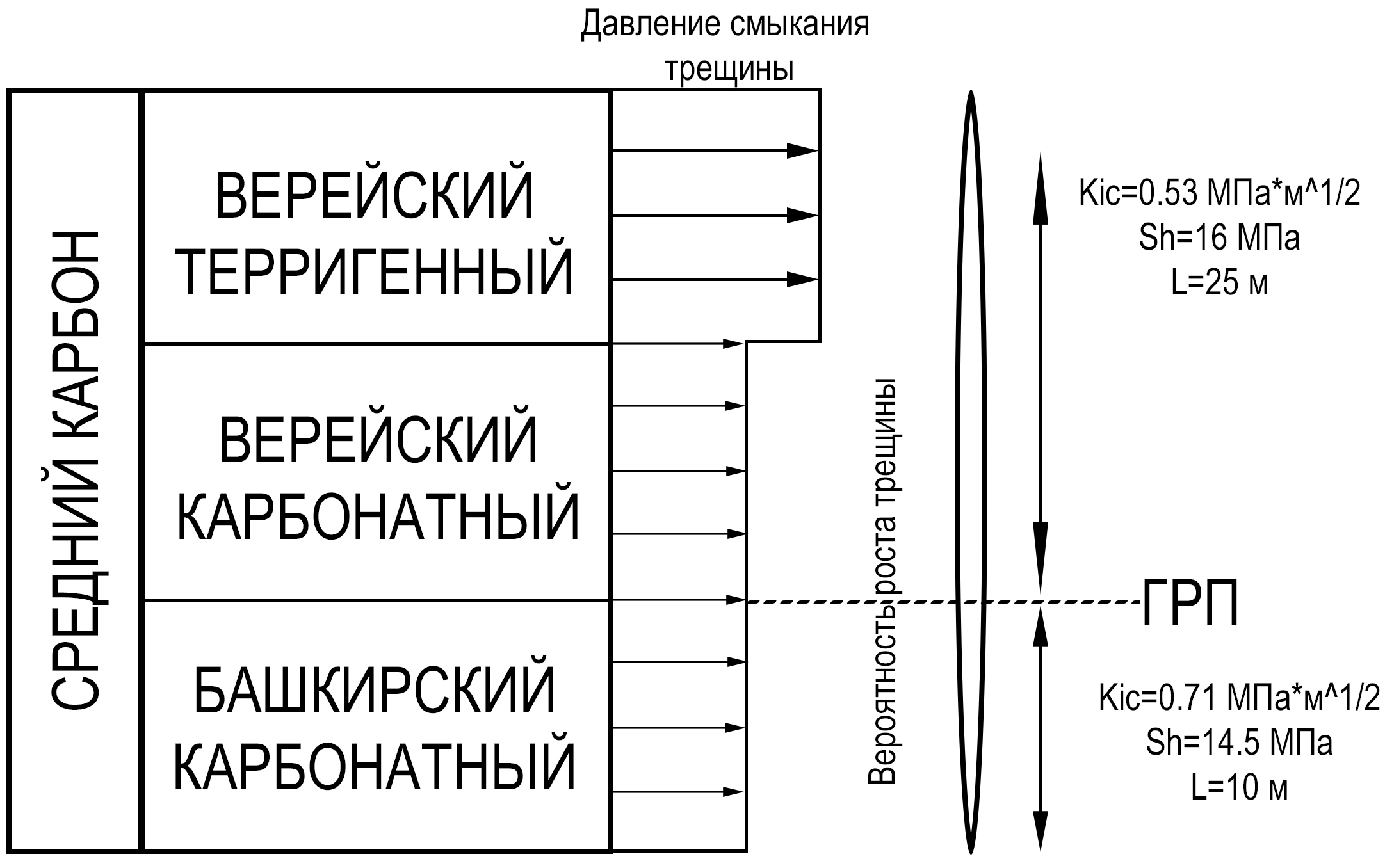
Рис. 9. Схема стратиграфического разреза в интервале гидроразрыва породы
Можно рассмотреть два варианта: 1) какое давление необходимо для роста трещины вверх, и 2) какое давление необходимо для роста трещины вниз. Результат моделирования изображен на рисунке 10 в виде зависимости давления внутри трещины (P–P0) и длины трещины. Зеленая кривая описывает рост трещины вверх, красная – рост трещины вниз.
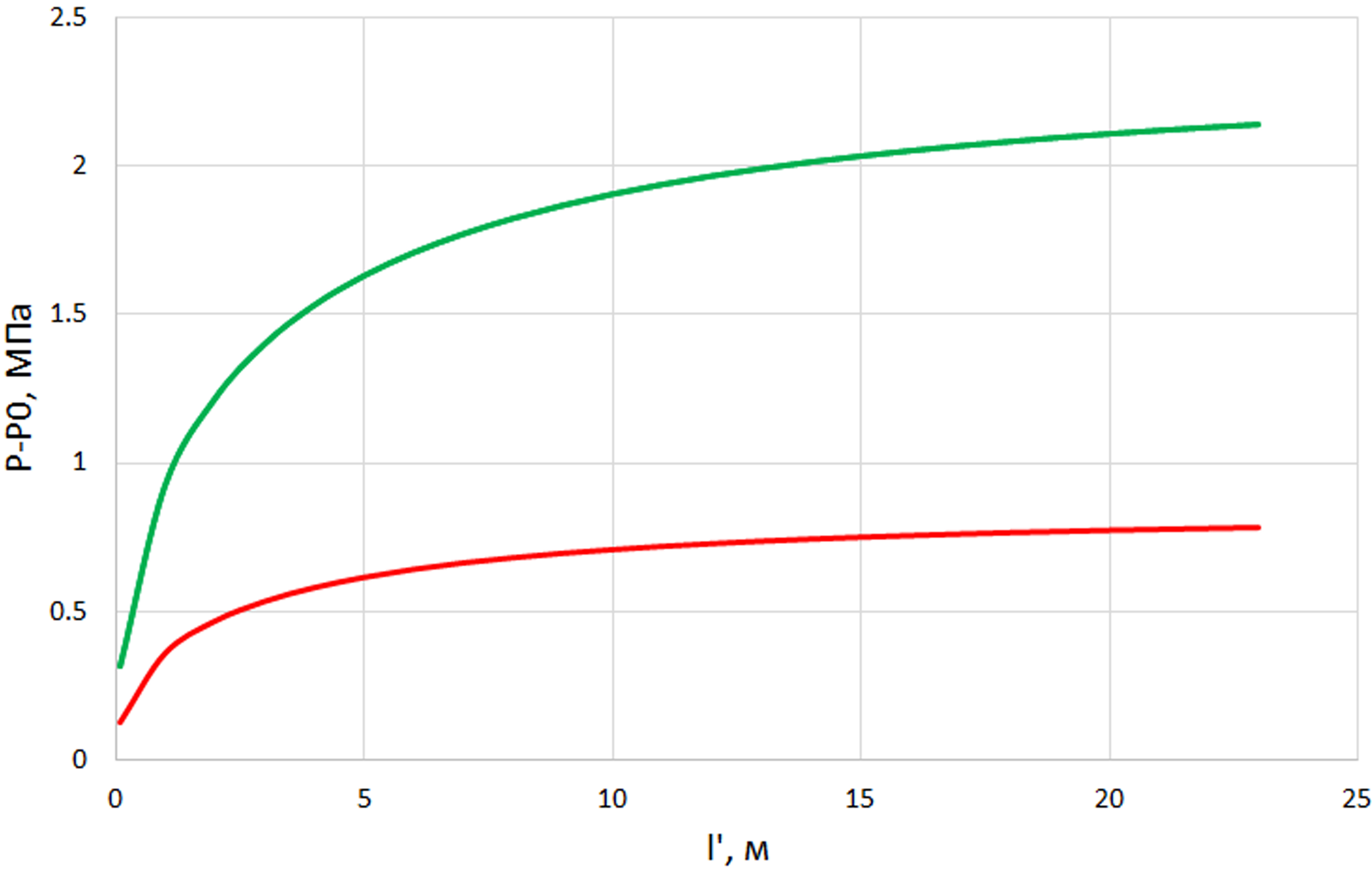
Рис. 10. График зависимости давления жидкости в трещине ГРП, превышающего минимальное главное напряжение, от ее длины. Зеленая кривая – рост трещины вверх, красная – рост трещины вниз.
Как было описано ранее, в данном случае рассматривается как вероятность роста трещины вверх по разрезу через отложения верейского горизонта, так и вниз по разрезу через отложения башкирского яруса. Оба случая могут оказаться негативными для добычи, так как повышается вероятность прорыва в водоносные горизонты и обводнения пласта. Рост трещины вверх по разрезу удерживается терригенной частью верейского горизонта, который обладает пониженной прочностью и повышенным давлением смыкания трещины. Распространение трещины вниз по разрезу удерживается повышенной прочностью пород башкирского яруса, однако давление смыкания трещины остается практически неизменным. Очевидно, что трещине «легче» распространиться вниз, для этого необходимо, чтобы внутри трещины давление стало выше на 0,8 МПа, чем давление смыкания (Shmin). Для того, чтобы трещина росла вверх, необходимо, чтобы давление внутри трещины превысило давление смыкания более чем на 2.2 МПа. Следовательно, основным фактором, удерживающим неконтролируемый рост трещины, является давление смыкания трещины или минимальное горизонтальное напряжение. Прочность породы оказывает вторичное влияние. Этот факт необходимо учитывать при планировании гидроразрыва пород. Следует внимательно относится к вычислению минимального горизонтального напряжения, учитывая всевозможные исследования, такие как результаты мини-ГРП, лабораторные исследования керна, обработка и интерпретация каротажных данных.
Заключение
В работе показан алгоритм изучения геомеханических свойств массивов горных пород нефтяного месторождения, представленного карбонатными отложениями. Комплексирование результатов лабораторных исследований, каротажных данных и результатов мини-ГРП позволило выполнить реконструкцию современных тектонических напряжений, действующих в околоскважинном пространстве. Помимо этого, представлена прикладная составляющая этой модели, а именно, моделирование роста трещины гидроразрыва с учетом напряженно-деформированного состояния горных пород. Наглядно показано, как влияют на рост трещины напряжения и механические свойства пород.
Финансирование
Работа выполнена при поддержке Минобрнауки России в рамках соглашения № 075-15-2022-299 о предоставлении гранта в форме субсидий из федерального бюджета на осуществление государственной поддержки создания и развития научного центра мирового уровня «Рациональное освоение запасов жидких углеводородов планеты».
Список литературы
1. Дубиня Н.В. (2019). Обзор скважинных методов изучения напряженного состояния верхних слоев Земной коры. Физика Земли, 2, c. 137–155.
2. Хисамов Р.С., Войтович Е.Д., Либерман В.Б., Гатиятуллин Н.С., Войтович С.Е. (2006). Тектоническое и нефтегеологическое районирование территории Татарстана. Казань: ФЭН, 328 с.
3. Муслимов Р.Х., Абдулмазитов Р.Г., Хисамов Р.Б. и др. (2007). Нефтегазоносность Республики Татарстан. Геология и разработка нефтяных месторождений. Казань: ФЭН, 316 с.
4. Afsari M., Ghafoori M.R., Roostaeian M., Haghshenas A., Ataei A., Masoudi R. (2009). Mechanical Earth Model (MEM): an effective tool for borehole stability analysis and managed pressure drilling (case study). SPE Middle East Oil Gas Show Conf. MEOS, Proc. OnePetro, vol. 1. pp. 87–98. doi: 10.2118/118780-MS
5. Brocher T.M. (2005). Empirical Relations between Elastic Wavespeeds and Density in the Earth’s Crust. Bulletin of the Seismological Society of America, 95(6), pp. 2081–2092. doi: 10.1785/0120050077
6. Gaarenstroom L., Tromp R.A.J., Brandenburg A.M. (1993). Overpressures in the Central North Sea: implications for trap integrity and drilling safety. Geological Society of London. Special Publications. Petroleum Geology Conference Series, 4(1), pp. 1305–1313. doi: 10.1144/0041305
7. Ismail N.I., Naz M.Y., Shukrullah S., Sulaiman S.A. (2020). Mechanical earth modeling and sand onset production prediction for Well X in Malay Basin. Journal of Petroleum Exploration and Production Technology, 10(7), pp. 2753–2758. doi: 10.1007/s13202-020-00932-2
8. Jimenez J.A., Chalaturnyk R.J., Whittaker S.G. (2005). A Mechanical earth model for the Weyburn CO<sub>2</sub> monitoring and storage project and its relevance to long-term performance assessment. Green-house Gas Control Technologies, pp. 2141–2145. doi: 10.1016/B978-008044704-9/50289-5
9. Ljunggren C., Chang Y., Janson T., Christiansson R. (2003). An overview of rock stress measurement methods. International Journal of Rock Mechanics and Mining Sciences, 40(7), pp. 975–989. doi: 10.1016/j.ijrmms.2003.07.003
10. Plumb R., Edwards S., Pidcock G., Lee D., Stacey B. (2000). The mechanical earth model concept and its application to high-risk well construction projects. Proceedings of IADC/SPE Drilling Conference. SPE, pp. 1–13. doi: 10.2118/59128-MS
11. Prats M. (1981). Effect of burial history on the subsurface horizontal stresses of formations having different material properties. Society of Petroleum Engineers Journal, 21(6), pp. 658–662. doi: 10.2118/9017-PA
12. Simonson E.R., Abou-Sayed A.S., and Clifton R.J. (1978). Containment of Massive Hydraulic Fractures. SPE J., 18, pp. 27–32. doi: 10.2118/6089-PA
13. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007-2014 (2015). Ed. R. Ulusay. Springer Cham Heidelberg New York Dordrecht London. doi: 10.1007/978-3-319-07713-0
14. Zain-Ulabedin M., Henk A. (2020). Building 1D and 3D Mechanical earth models for underground gas storage – a case study from the Molasse Basin, Southern Germany. Energies, 13, pp. 1–21. doi: 10.3390/en13215722
15. Zoback M.D., Barton C.A., Brudy M., Castillo D.A., Finkbeiner T., Grollimund B.R., Moos Peska D.B., Ward C.D., Wiprut D.J. (2003). Determination of stress orientation and magnitude in deep wells. International Journal of Rock Mechanics and Mining Sciences, 40(7–8), pp. 1049–1076. doi: 10.1016/j.ijrmms.2003.07.001
Об авторах
Э. Р. ЗиганшинРоссия
Эдуард Ришадович Зиганшин, кандидат геол.-минерал. наук, старший научный сотрудник
Институт геологии и нефтегазовых технологий
420111; ул. Кремлевская, д. 4/5; Казань
В. Е. Косарев
Россия
Виктор Евгеньевич Косарев, старший преподаватель
Институт геологии и нефтегазовых технологий
420111; ул. Кремлевская, д. 4/5; Казань
А. В. Фаттахов
Россия
Артур Вилданович Фаттахов, старший преподаватель
Институт геологии и нефтегазовых технологий
420111; ул. Кремлевская, д. 4/5; Казань
С. И. Гильфанов
Россия
Салават Ильдусович Гильфанов, инженер
Институт геологии и нефтегазовых технологий
420111; ул. Кремлевская, д. 4/5; Казань
М. А. Скоробогатова
Россия
Марта Андреевна Скоробогатова, инженер
Институт геологии и нефтегазовых технологий
420111; ул. Кремлевская, д. 4/5; Казань
А. Д. Маликов
Россия
Азат Дамирович Маликов, главный геолог
423458; ул. Маяковского, д. 116; Альметьевск
А. С. Сергеев
Россия
Александр Станиславович Сергеев, начальник отдела
геологический отдел
423458; ул. Маяковского, д. 116; Альметьевск
Рецензия
Для цитирования:
Зиганшин Э.Р., Косарев В.Е., Фаттахов А.В., Гильфанов С.И., Скоробогатова М.А., Маликов А.Д., Сергеев А.С. Особенности реконструкции современных напряжений в карбонатных породах на примере нефтяного месторождения Республики Татарстан. Георесурсы. 2025;27(1):135-143. https://doi.org/10.18599/grs.2025.1.11
For citation:
Ziganshin E.R., Kosarev V.E., Fattakhov A.V., Gilfanov S.I., Skorobogatova M.A., Malikov A.D., Sergeev A.S. Features of Stress State Reconstruction in Carbonate Rocks on the Example of an Oil Field of the Republic of Tatarstan. Georesursy = Georesources. 2025;27(1):135-143. (In Russ.) https://doi.org/10.18599/grs.2025.1.11















.png)


