Перейти к:
Оценка параметров закачки диоксида углерода в насыщенный пористый пласт с неоднородной проницаемостью при наличии гидратообразования
https://doi.org/10.18599/grs.2025.3.10
Аннотация
Одним из эффективных методов борьбы с ростом концентрации диоксида углерода в атмосфере является его секвестрация в пористых средах в твердой газогидратной форме. Уникальные свойства газовых гидратов, такие как их высокая газоемкость, низкая проницаемость и естественная стабильность, делают их привлекательным вариантом для долговременного захоронения СО2 . В статье в рамках рассмотрения проблематики организации геологического газогидратного хранилища диоксида углерода записана математическая модель, позволяющая осуществить теоретическое изучение процесса образования гидрата СО2 при его закачке в пласт, поры которого в исходном состоянии заняты метаном и водой. В предложенной математической модели осуществлен учет зональной неоднородности пористого коллектора, течения в нем при наличии фазовых превращений (гидратообразование и растворимость диоксида углерода в воде) газовой (СН4 и/или СО2 ) и жидкой (вода и растворенный CO2 ) фаз, переноса тепла из рассматриваемой области пласта в окружающие горные породы; процесс гидратообразования рассматривается как равновесный фазовый переход. Представлены расчетные уравнения для изучаемого в работе процесса и построены численные решения задачи, описывающие распределения параметров (температуры, давления, насыщенностей фаз) в пласте. Расчетным путем показано, что при закачке СО2 в пласт в нем возможно формирование нескольких характерных зон, отличающихся по составу насыщающих их флюидов. Продемонстрирована необходимость учета при описании температурного поля в пласте таких факторов, как теплота, выделяемая при фазовых переходах, эффект Джоуля-Томсона, теплообмен пористого коллектора с окружающими горными породами. Приведены и проанализированы результаты вычислительных экспериментов при размещении нагнетательной скважины в высоко- или низкопроницаемом участке пористого коллектора. Проведенное численное исследование показало, что для организации эффективного газогидратного хранения диоксида углерода необходимы пористые среды с достаточно высокими значениями проницаемости.
Ключевые слова
Для цитирования:
Мусакаев Н.Г., Бородин С.Л. Оценка параметров закачки диоксида углерода в насыщенный пористый пласт с неоднородной проницаемостью при наличии гидратообразования. Георесурсы. 2025;27(3):121-129. https://doi.org/10.18599/grs.2025.3.10
For citation:
Musakaev N.G., Borodin S.L. Estimation of the parameters of carbon dioxide injection into a saturated porous reservoir with heterogeneous permeability in the presence of hydrate formation. Georesursy = Georesources. 2025;27(3):121-129. https://doi.org/10.18599/grs.2025.3.10
Введение
С ростом глобальной индустриализации и чрезмерной эксплуатацией невозобновляемых источников энергии произошло высвобождение большого количества парниковых газов, в первую очередь, диоксида углерода (Xu et al., 2020). Работы ряда исследователей показали, что в настоящее время одним из лучших вариантов для крупномасштабного сокращения данных выбросов является геологическое хранение CO2 (Kim, Santamarina, 2014; Lu et al., 2021). Согласно определению, приведенному в статье (Корзун и др., 2023), под природным геологическим объектом подразумевается естественная геологическая система, которая может в течение достаточно длительного промежутка времени удержать парниковый газ в стабильном состоянии, без опасности возникновения аварийных ситуаций, связанных с выходом утилизируемых выбросов из коллекторов на поверхность. Мероприятия по утилизации и хранению диоксида углерода в пористых коллекторах включают в себя улавливание СО2, выделяемого промышленными или энергетическими предприятиями, и последующее его подземное хранение (Cao et al., 2022). Длительное хранение диоксида углерода в газообразном состоянии может привести к прорыву газа к поверхности и, соответственно, к непредсказуемым экологическим проблемам (Mac Dowell et al., 2017). Поэтому наиболее приемлемым вариантом является геологическое хранение диоксида углерода в твердой газогидратной форме (Kim, Santamarina, 2014; Hassanpouryouzband et al., 2019; Zhou et al., 2024). Эффективность такого хранения CO2 может быть обусловлена тем обстоятельством, что при одинаковых термодинамических условиях в единице объема газового гидрата может содержаться в несколько раз больше газа, чем в газообразном состоянии (Истомин, Якушев, 1992; Чувилин, Гурьева, 2009; Makogon, 2010). Подземное газогидратное хранение диоксида углерода отвечает основным характеристикам возможного варианта организации такого хранилища, а именно: большая емкость хранения, долгосрочная изоляция CO2 (не менее нескольких сотен лет), разумная стоимость, минимальное воздействие на окружающую среду (Aminu et al., 2017). В качестве косвенного доказательства приведенных тезисов можно привести то обстоятельство, что, например, в северных российских регионах присутствуют природные скопления гидратов метана, оценочный возраст которых достигает сотни тысяч лет. При этом важно отметить, что область значений давлений и температур, при которых может стабильно существовать гидрат CO2, значительно шире, чем у гидрата CН4, что свидетельствует о возможности аналогичного длительного хранения диоксида углерода в газогидратном состоянии.
В настоящее время заинтересованность к проектам геологического хранения диоксида углерода имеют крупные корпорации в ряде стран. При организации хранилища CO2 важным является вопрос выбора резервуаров, подходящих для подземного газогидратного хранения диоксида углерода (Lu et al., 2021). Такими площадками могут служить истощенные месторождения углеводородного сырья (Корзун и др., 2023; Zhou et al., 2024), расположенные в относительной близости от предприятий, являющихся источниками выбросов СО2, например, от производителей электроэнергии и тепла.
Хранение диоксида углерода в истощенных нефтяных и газовых резервуарах считается одним из наиболее эффективных вариантов хранения из-за нескольких причин: 1) данные залежи были тщательно изучены до и во время отбора углеводородов; 2) имеется наземная и подземная инфраструктура, например, нагнетательные скважины и трубопроводы, они могут быть использованы для процесса захоронения либо напрямую, либо с небольшими изменениями; 3) нагнетание диоксида углерода в нефтенасыщенный пласт в качестве метода повышения нефтеотдачи и так применяется в нефтегазовой промышленности, и, следовательно, такой опыт может быть использован для процесса захоронения CO2 (Aminu et al., 2017; Ибрагимов и др., 2024).
Рациональное формирование подземного газогидратного хранилища диоксида углерода диктует необходимость в углубленном предварительном исследовании аспектов неизотермического газожидкостного течения в насыщенных пористых пластах при наличии фазовых переходов, а также анализа факторов, определяющих эффективность технологии такого хранения CO2. Например, одним из таких факторов является неоднородность пласта по проницаемости (Баренблатт и др., 2016; Hu et al., 2021). В этой связи важными представляются математическое моделирование и численное исследование процессов, происходящих при неизотермическом течении диоксида углерода в пористых средах с неоднородной проницаемостью с учетом образования газовых гидратов.
Методы
В работе методами математического моделирования изучены особенности неизотермической фильтрации газожидкостной смеси с учетом образования газового гидрата при нагнетании диоксида углерода в пористый пласт, поры которого в начальном состоянии заполнены метаном и водой. В первую очередь рассмотрим постановку задачи.
Рассмотрим в двумерном (радиальная ось r и вертикальная ось z) осесимметричном приближении процесс нагнетания CO2 в пористый пласт высотой H и радиусом R (рис. 1).
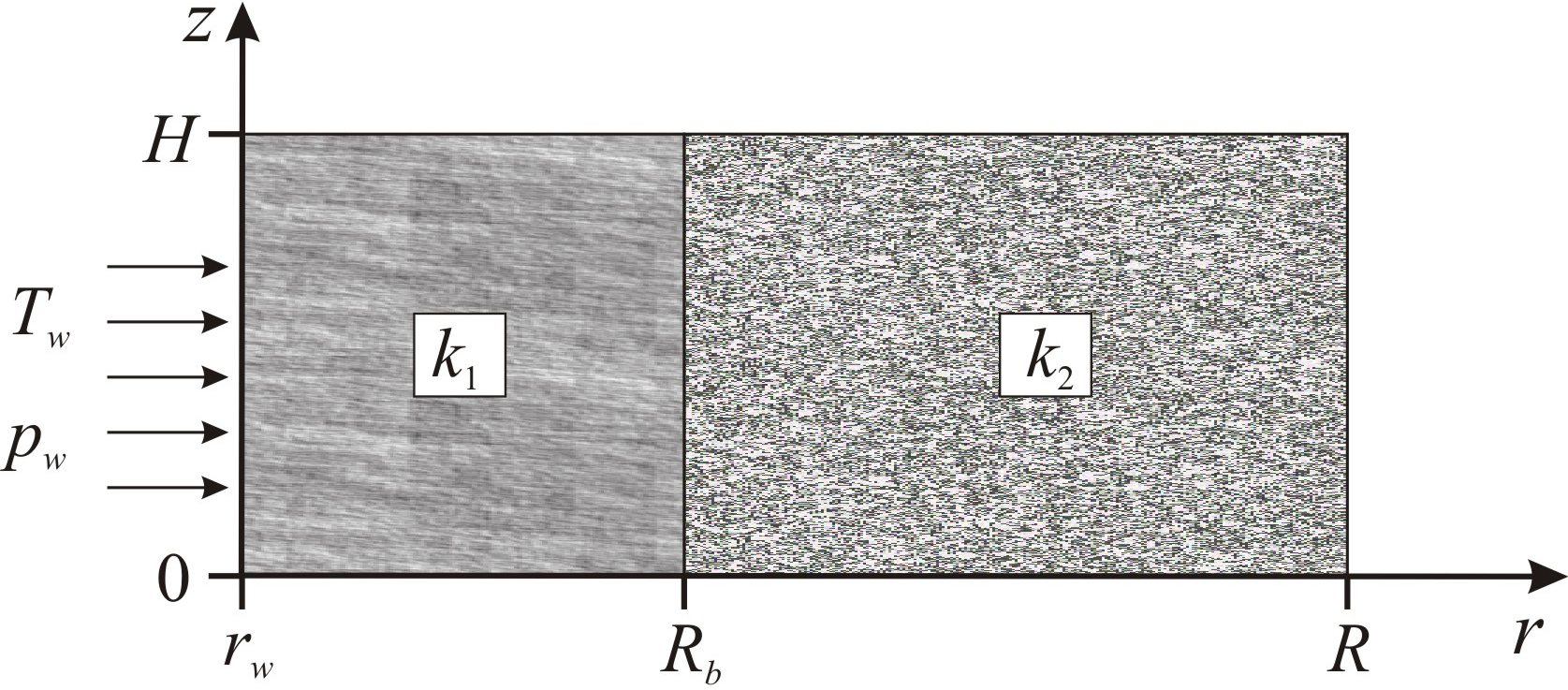
Рис. 1. Схематичное представление задачи: z и r – вертикальная и радиальная координаты; H, rw, Rb и R – высота пласта, радиус скважины, радиус первой зоны и радиус пласта соответственно; k1 и k2 – проницаемость первой и второй зоны; Tw и pw – температура закачиваемого диоксида углерода и давление его закачки
Пусть закачка газа осуществляется через скважину радиуса rw, которая вскрывает пласт на всю его высоту. Внешние границы пласта являются непроницаемыми для вещества, однако через них может происходить теплообмен с окружающими породами за счет теплопроводности. Пусть рассматриваемая сплошная среда в исходном состоянии состоит из трех фаз: из твердого каркаса (скелета), не участвующего в физико-химических превращениях, метана и воды с известной насыщенностью. Скелет пористой среды полагаем неподвижным и несжимаемым. Примем, что в начальный момент времени температура в рассматриваемом пласте и окружающих его горных породах равна T0. Фильтрация возможна только в пористом пласте, исходное давление в нем p0. Рассматриваемый пласт состоит из двух зон с различной проницаемостью k1 и k2. Пусть нагнетание диоксида углерода осуществляется при постоянном давлении pw, при этом температура на забое скважины Tw имеет постоянное значение, меньшее равновесной температуры образования гидрата CO2 для давления pw (рис. 1).
При математическом моделировании двухфазной фильтрации с учетом образования гидрата CO2 примем следующие основные допущения: газовый гидрат рассматривается как система, состоящая из воды и газа, и массовая концентрация газа в газовом гидрате G постоянна; метан не растворяется в воде; пренебрегаем испарением воды; рассматривается однотемпературная модель (температуры всех фаз в некотором малом объеме равны); пористость пласта для обеих зон пласта одинакова и постоянна; плотность воды и удельные теплоты фазовых переходов являются постоянными величинами; капиллярные эффекты не учитываются (Басниев и др., 1993; Bondarev et al., 2018). При изучении процесса закачки CO2 в пласт в отличие от работ (Цыпкин, 2014; Khasanov et al., 2019; Khasanov et al., 2020) учитывается растворимость CO2 в воде, фильтрация воды и газа, теплообмен пористого коллектора с окружающими горными породами.
Расчетные уравнения для изучаемого в работе процесса могут быть записаны на основе уравнений сохранения масс, закона Дарси, уравнения сохранения энергии (Нигматулин, 1987; Басниев и др., 1993; Бородин, Бельских, 2020; Musakaev, Borodin, 2023). При этом уравнение пьезопроводности и уравнение притока тепла, на основе которых происходит расчет изменения давления и температуры, соответственно, в отличие от работы (Musakaev, Borodin, 2023) содержат слагаемые, учитывающие интенсивность растворения диоксида углерода в воде Jgl. Соотношение для нахождения этой величины может быть записано следующим образом:
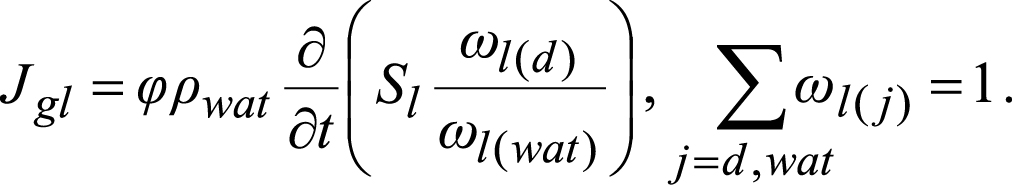
Здесь и далее индексы j = sk, g, l, h, d, m и wat относятся к параметрам скелета пористой среды, газовой фазы, жидкой фазы, газового гидрата, диоксида углерода, метана и воды, соответственно; нижние индексы в скобках означают составляющие соответствующей фазы. Jgl – интенсивность растворения CO2 в воде, кг/(м³·с); Sj ( j = g, l, h) – насыщенность пор j-ой фазой; φ – пористость пласта; ρwat – плотность воды, кг/м³; ωl(d) и ωl(wat) – массовое содержание диоксида углерода и воды в жидкой фазе, соответственно.
Используются следующие уравнения состояния для жидкой и газовой фаз (Shagapov et al., 2012; Бородин, Бельских, 2020):
![]()
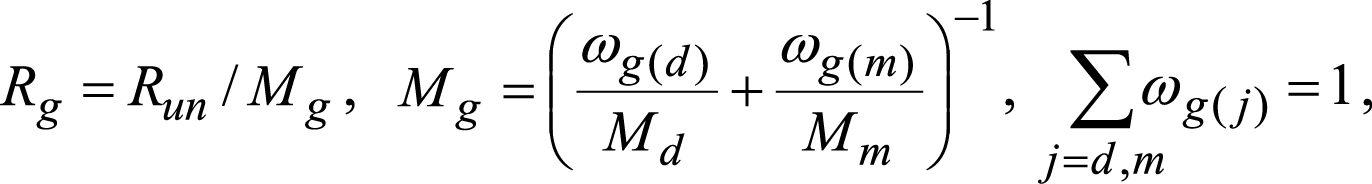
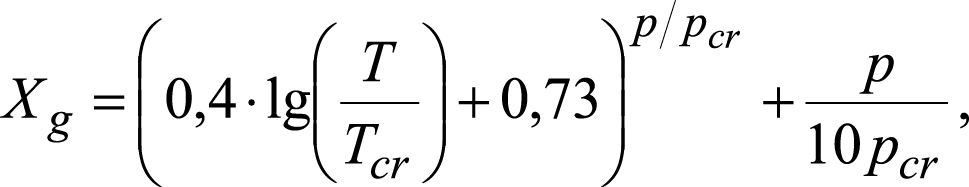
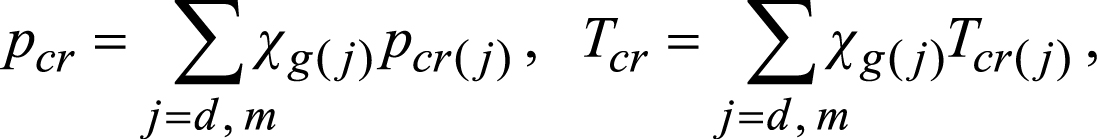

где p – давление, Па; T – температура, К; ρj ( j = sk, g, l, h) – плотность j-ой фазы, кг/м³; Rg – удельная газовая «постоянная» (этот параметр может изменяться в зависимости от состава газовой фазы), Дж/(кг·К); Run – универсальная газовая постоянная, Дж/(моль·К); Md и Mm – молярная масса диоксида углерода и метана, кг/моль; ωg(d) и ωg(m) – массовое содержание CO2 и CH4 в газовой смеси; Tcr и pcr – критическое значение температуры (К) и давления (Па) для газовой фазы; Tcr(d) и Tcr(m) – критическое значение температуры для углекислого газа и метана, К; pcr(d) и pcr(m) – критическое значение давления для CO2 и CH4, Па; χg(d) и χg(m) – мольная доля диоксида углерода и метана в газовой смеси.
Проницаемость пористой среды можно найти из соотношения (Zhang et al., 2022):
k = k0(1 – Sh)n,
где k0 – тензор проницаемости пористой среды при отсутствии газового гидрата, м²; n – показатель степени, зависящий от типа заполнения газогидратом порового пространства пласта. При проведении расчетов принято n = 3.
В работе принимается, что образование гидрата CO2 происходит в равновесном режиме (Borodin et al., 2022). Для нахождения массовой концентрации диоксида углерода в воде в зависимости от парциального давления этого газа и температуры используются эмпирические соотношения из работы (Воронов и др., 2011).
Результаты
Следующим шагом исследования процесса хранения диоксида углерода в геологических формациях в твердой газогидратной форме стало проведение вычислительных экспериментов по изучению особенностей образования гидрата CO2 при закачке диоксида углерода в пласт, в исходном состоянии насыщенный водометановой смесью. Эти расчеты производились на основе авторского компьютерного кода, численно реализующую математическую модель. Методика расчета параметров изучаемого процесса представлена авторами на Первой Российской газогидратной конференции «Газовые гидраты – энергия будущего» (Бородин, Мусакаев, 2024), и она аналогична методике, изложенной в работе (Musakaev et al., 2020). Значения параметров, используемые при проведении расчетов (если не указано дополнительно), приведены в табл. 1 (Истомин, Якушев, 1992; Бородин, Бельских, 2020; Misyura et al., 2023).

Табл. 1. Основные расчетные параметры
На рис. 2 представлены поля давления, температуры, насыщенности гидратом CO2, массовой доли CO2 в газовой смеси и массовой доли растворенного CO2 в воде для трех случаев (рис. 1).
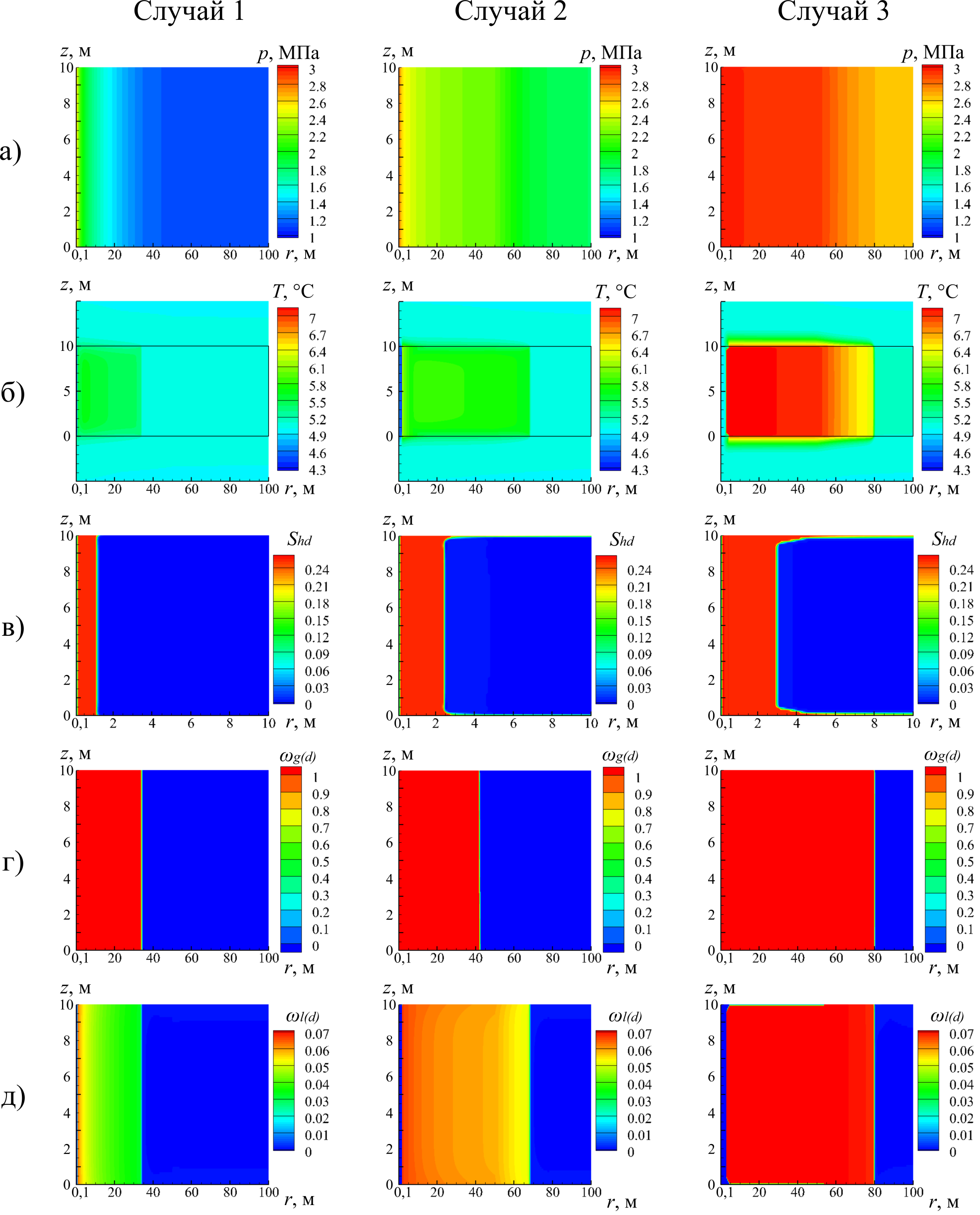
Рис. 2. Распределения в пласте давления p (а), температуры T (б), гидратонасыщенности Shd (в), массовой доли CO2 в газовой смеси ωg(d) (г) и массовой доли растворенного CO2 в воде ωl(d) (д). Распределения параметров построены на 7 сутки после начала закачки диоксида углерода пласт
Случай 1. Нагнетательная скважина, через которую происходит закачка диоксида углерода в пласт, расположена в низкопроницаемой зоне, при этом значение проницаемости k1 = 10-14 м², значение проницаемости для высокопроницаемой зоны k2 = 10-13 м².
Случай 2. Нагнетательная скважина размещена в высокопроницаемой зоне, при этом k1 = 10-13 м², k2 = 10-14 м².
Случай 3. Нагнетательная скважина также расположена в высокопроницаемой зоне, но k1 = 10-12 м², k2 = 10-14 м².
На рис. 3 Представлены распределения параметров по радиальной координате r для средней по высоте линии пласта (при z = H/2).

Рис. 3. Распределения по r при z = H/2 давления p (а), температуры T (б), гидратонасыщенности Shd (в), массовой доли CO2 в газовой смеси ωg(d) (г) и массовой доли растворенного CO2 в воде ωl(d) (д) на 7 сутки после начала закачки диоксида углерода пласт
На рис. 4 представлено изменение со временем массы CO2 в пласте.
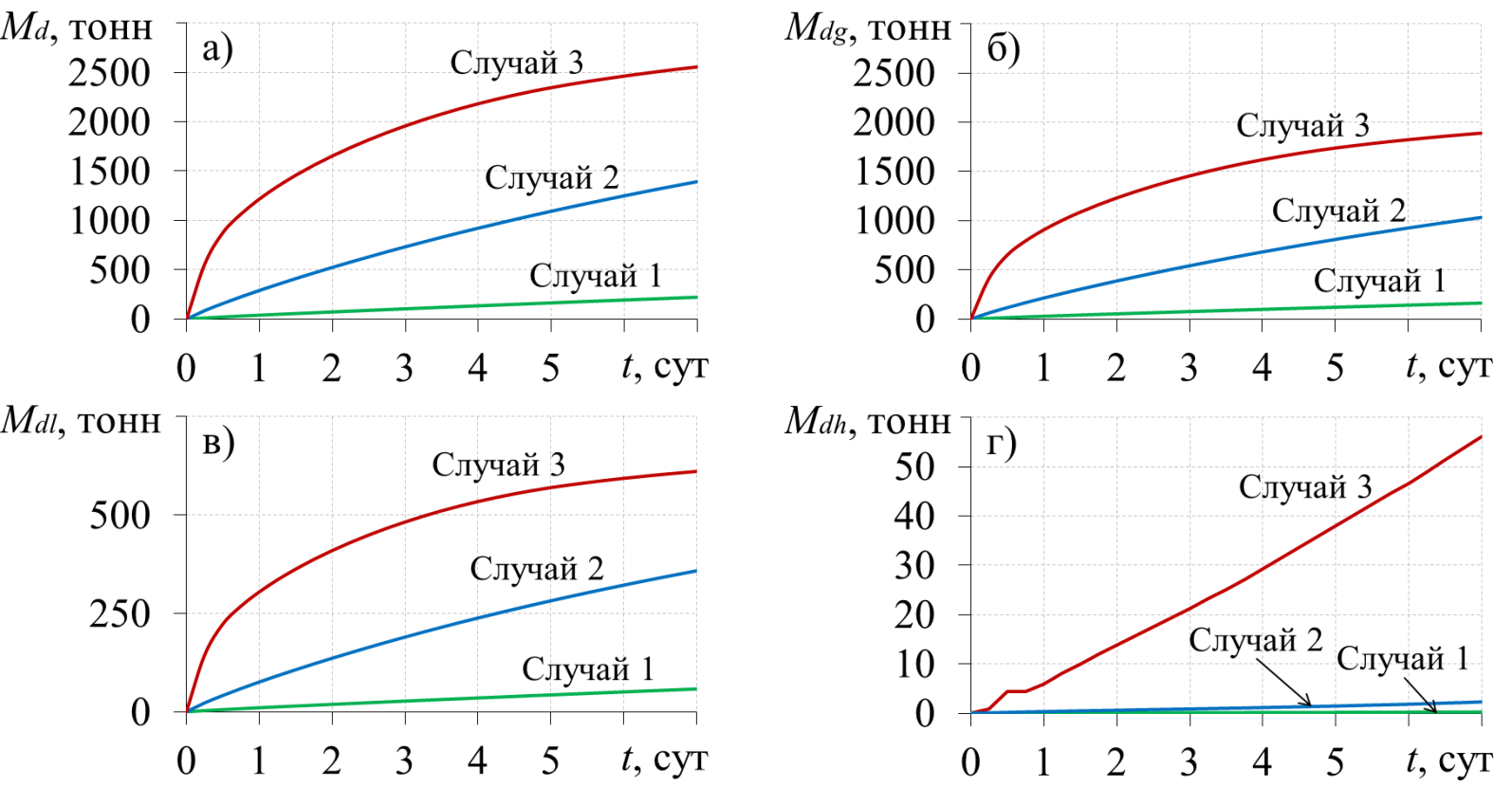
Рис. 4. Динамика изменения накопленной массы диоксида углерода в пласте: а) суммарная масса; б) в газообразном состоянии; в) в растворенном виде в воде; г) в составе газового гидрата
Обсуждение результатов
Из данных, представленных на рис. 2 и 3, видно, что закачиваемый в пористый пласт диоксид углерода вытесняет метан вглубь пласта. В пласте, поры которого до начала нагнетания СО2 заняты метаном и водой, диоксид углерода присутствует в трех состояниях: в составе газового гидрата, в растворенном виде в воде и в газообразном состоянии.
Гидратообразование происходит в основном в зоне, примыкающей к нагнетательной скважине, в этой области пласта в порах присутствуют диоксид углерода и его гидрат. Дальше (по координате r) поровое пространство заполнено СО2, гидратом СО2, водой; затем диоксидом углерода и водой; далее газовой фазой (CO2+CН4) и водой; и наконец, водометановой смесью. В первых двух отмеченных зонах из-за газогидратных отложений коллекторские свойства пласта ухудшаются, что приводит к снижению темпов фильтрации от скважины в пласт и большому градиенту давления в области с присутствием газового гидрата. Для случая расположения нагнетательной скважины в высокопроницаемой зоне (Случаи 2 и 3) вышеописанный фактор оказывает меньшее влияние, и давление во всем пласте существенно увеличивается (даже в отдаленной от скважины низкопроницаемой зоне), что свидетельствует о лучшем проникновении диоксида углерода в пласт. Также из рис. 2 и 3 видно, что температура в пласте ведет себя немонотонно. Это связано с влиянием на нее следующих факторов: эффект Джоуля-Томсона (в области больших градиентов давления температура при фильтрации реального газа существенно снижается); выделение тепла при образовании гидрата СО2; выделение тепла при растворении диоксида углерода в воде. Видно, что вблизи скважины температура снижается ниже начальной, так как в этой области наблюдается наибольший перепад давления, что приводит к наиболее интенсивному охлаждению вследствие эффекта Джоуля-Томсона. Далее наблюдается повышение температуры выше начальной вследствие фазовых переходов. Во всем пласте, где одновременно присутствуют диоксид углерода и вода, наблюдается повышение температуры выше начальной вследствие выделения тепла при растворении этого газа в воде. Причем вблизи верхней и нижней границ пласта температуры ниже, а количество растворенного CO2 в воде выше, что объясняется теплоотдачей в окружающие непроницаемые для вещества породы за счет теплопроводности. В зоне, примыкающей к нагнетательной скважине, вся вода переходит в состав газогидрата, что связано, в первую очередь, с существенным снижением температуры в этой части пласта вследствие действия эффекта Джоуля-Томсона. Таким образом, для адекватного описания температурного поля в пласте необходим учет таких факторов, как теплота, выделяемая при фазовых переходах, эффект Джоуля-Томсона, теплообмен рассматриваемого пористого коллектора с окружающими горными породами. Рисунки 2 и 3 также показывают, что вытеснение метана диоксидом углерода происходит практически в поршневом режиме. Размеры области, в которой в газовой фазе одновременно находятся CO2 и CН4, малы по сравнению с протяженностью пласта; поршневой характер вытеснения обусловлен тем, что вязкость CO2 в полтора раза выше вязкости CH4 (Цыпкин, 2014).
Из данных, представленных на рис. 4, видно, что масса захороненного диоксида углерода тем выше, чем выше проницаемость призабойной зоны скважины, поэтому при организации такого способа утилизации CO2 необходимо осуществлять закачку этого газа в высокопроницаемые зоны, т.е. для захоронения диоксида углерода с большей интенсивностью нагнетательную скважину желательно располагать в области пласта с наибольшей проницаемостью. Анализ рис. 2 и 3 позволяет сделать вывод о том, что для принятых в работе параметров, для организации эффективного газогидратного хранения диоксида углерода необходимы пористые среды с достаточно высокими значениями проницаемости. В противном случае, во-первых, вследствие низкой проницаемости время закачки необходимого объема CO2 будет существенно увеличиваться, и, во-вторых, образовавшийся газогидрат будет еще больше снижать проницаемость пористой среды, что может привести к практически полной остановке дальнейшей фильтрации CO2.
Для рассмотренного набора параметров при размещении нагнетательной скважины в низкопроницаемой зоне (k1 = 10–14 м²) диоксид углерода в составе газового гидрата на конечный момент времени (7 суток) составляет величину около 300 кг. Если же нагнетательная скважина расположена в высокопроницаемой зоне (k1 = 10–13 м²), то этот показатель имеет величину около 2300 кг. При дальнейшем увеличении проницаемости (Случай 3) накопленная масса диоксида углерода в составе газового гидрата составляет величину уже около 56000 кг. Однако, как видно, из рис. 4 для всех рассмотренных случаев масса CO2 в составе газового гидрата меньше его массы в свободном и растворенном состоянии. Это связано с тем, что на процесс образования газового гидрата в пласте существенное влияние оказывают (помимо коллекторских свойств) исходные термодинамические параметры подземного хранилища CO2. Т.е. необходимы дополнительные исследования по определению пластов с наиболее благоприятными для гидратообразования начальными термодинамическими условиями, а также по выявлению наиболее эффективных параметров закачки диоксида углерода. И комплексный учет всех этих факторов позволит обеспечить наиболее эффективное подземное газогидратное захоронение CO2.
Заключение
Статья посвящена изучению особенностей процесса хранения диоксида углерода в геологических формациях в твердой газогидратной форме. Предложена в двумерном осесимметричном приближении математическая модель неизотермической фильтрации газожидкостной смеси, в которой в отличие от предыдущих работ произведен дополнительный учет таких факторов, как наличие в пласте зон с различной проницаемостью, двухфазная фильтрация, растворимость CO2 в воде, теплоотдача (за счет кондуктивного теплообмена) из рассматриваемой области пористой среды в окружающие горные породы, неизотермические эффекты. Расчетным путем показано, что при закачке диоксида углерода в пористый пласт распределение температуры по длине пласта имеет немонотонный характер, обусловленный действием эффекта Джоуля-Томсона, выделением тепла при образовании гидрата СО2 и растворении данного газа в воде. Вблизи верхней и нижней границ пласта температуры ниже, а количество растворенного CO2 в воде выше, что объясняется теплоотдачей в окружающие непроницаемые для вещества породы за счет теплопроводности. Показано, что для более эффективной организации газогидратного хранения диоксида углерода в зонально-неоднородном пористом пласте необходимо располагать нагнетательную скважину в зоне с большими значениями проницаемости.
Финансирование
Исследование выполнено за счет гранта Российского научного фонда № 24-29-00093, https://rscf.ru/project/24-29-00093/
Публикация статьи поддержана Министерством науки и высшего образования Российской Федерации по соглашению № 075-10-2022-011 в рамках программы развития НЦМУ.
Список литературы
1. Баренблатт Г.И., Лобковский Л.И., Нигматулин Р.И. (2016). Математическая модель истечения газа из газонасыщенного льда и газогидратов. Доклады Академии наук, 470 (4), с. 458–461. https://doi.org/10.7868/S0869565216280148
2. Басниев К.С., Кочина И.Н., Максимов В.М. (1993). Подземная гидромеханика. М.: Недра, 416 с. Бородин С.Л., Бельских Д.С. (2020). Математическое моделирование равновесного полного замещения метана углекислым газом в газогидратном пласте при отрицательных температурах. Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика, 6 (2). с. 63–80. https://doi.org/10.21684/2411-7978-2020-6-2-63-80
3. Бородин С.Л., Мусакаев Н.Г. (2024). Методика расчета параметров процесса закачки углекислого газа в зонально-неоднородный пористый пласт с учетом образования газового гидрата. Материалы Первой Российской газогидратной конференции «Газовые гидраты – энергия будущего» (РГК I). СПб.: ВНИИОкеангеология, c. 51–56. https://doi.org/10.24412/cl-37274-2024-1-51-56
4. Воронов В.П., Городецкий Е.Е., Григорьев Б.А., Муратов А.Р. (2011). Экспериментальное исследование процесса замещения метана в газовом гидрате диоксидом углерода. Вести газовой науки, 2(7), с. 235–248.
5. Ибрагимов И.И., Индрупский И.М., Гарифуллина Ч.А., Халиуллин Т.Ф., Валиуллин И.В., Залятдинов А.А., Садреева Р. Х., Бурлуцкий Е.А., Мингазутдинов А.Н., Ремеев М.М., Кашапов И.Х. (2024). Экспериментальная оценка эффективности вытеснения нефти дымовыми газами для объекта разработки в карбонатных отложениях Урало-Поволжского региона. Георесурсы, 26 (1), с. 127–135. https://doi.org/10.18599/grs.2024.1.11
6. Истомин В.А., Якушев В.С. (1992). Газовые гидраты в природных условиях. М.: Недра, 235 с. Корзун А.В., Ступакова А.В., Харитонова Н.А., Асеева А.В., Осипов К.О., Пронина Н.В., Макарова Е.Ю., Вайтехович А.П., Лопатин А.Ю., Карпушин М.Ю., Перегудов Ю.Д., Сауткин Р.С., Большакова М.А., Ситар К.А., Редькин А.С. (2023). Применимость природных геологических объектов для хранения, захоронения и утилизации углекислого газа (обзор). Георесурсы, 25 (2), с. 22–35. https://doi.org/10.18599/grs.2023.2.2
7. Нигматулин Р.И. (1987). Динамика многофазных сред. М.: Наука. Цыпкин Г.Г. (2014). Математическая модель инжекции углекислого газа в пласт с образованием гидрата. Доклады Академии наук, 458(4), с. 422–425. https://doi.org/10.7868/S0869565214220113
8. Чувилин Е.М., Гурьева О.М. (2009). Экспериментальное изучение образования гидратов СО2 в поровом пространстве промерзающих и мерзлых пород. Криосфера Земли, 13(3), с. 70–79.
9. Aminu M.D., Nabavi S.A., Rochelle C.A., Manovic V. (2017). A review of developments in carbon dioxide storage. Applied Energy, 208, pp. 1389– 1419. https://doi.org/10.1016/j.apenergy.2017.09.015
10. Bondarev E.A., Rozhin I.I., Popov V.V., Argunova K.K. (2018). Underground Storage of Natural Gas in Hydrate State: Primary Injection Stage. Journal of Engineering Thermophysics, 27 (2), pp. 221–231. https://doi.org/10.1134/S181023281802008X
11. Borodin S.L., Musakaev N.G., Belskikh D.S. (2022). Mathematical Modeling of a Non-Isothermal Flow in a Porous Medium Considering Gas Hydrate Decomposition: A Review. Mathematics, 10(24), 4674. https://doi.org/10.3390/math10244674
12. Cao X., Wang H., Yang K., Wu S., Chen Q., Bian J. (2022). Hydratebased CO2 sequestration technology: Feasibilities, mechanisms, influencing factors, and applications. Journal of Petroleum Science and Engineering, 219, 111121. https://doi.org/10.1016/j.petrol.2022.111121
13. Hassanpouryouzband A., Yang J., Tohidi B., Chuvilin E., Istomin V., Bukhanov B. (2019). Geological CO2 Capture and Storage with Flue Gas Hydrate Formation in Frozen and Unfrozen Sediments: Method Development, Real Time-Scale Kinetic Characteristics, Efficiency, and Clathrate Structural Transition. ACS Sustainable Chemistry & Engineering, 7(5), pp. 5338–5345. https://doi.org/10.1021/acssuschemeng.8b06374
14. Hu T., Xu T., Tian H., Zhou B., Yang Y. (2021) A study of CO2 injection well selection in the naturally fractured undulating formation in the Jurong Oilfield, China. International Journal of Greenhouse Gas Control, 109, 103377. https://doi.org/10.1016/j.ijggc.2021.103377
15. Khasanov M.K., Musakaev N.G., Stolpovsky M.V., Kildibaeva S.R. (2020). Mathematical Model of Decomposition of Methane Hydrate during the Injection of Liquid Carbon Dioxide into a Reservoir Saturated with Methane and Its Hydrate. Mathematics, 8 (9), 1482. https://doi.org/10.3390/math8091482
16. Khasanov M.K., Stolpovsky M.V., Gimaltdinov I.K. (2019). Mathematical model of injection of liquid carbon dioxide in a reservoir saturated with methane and its hydrate. International Journal of Heat and Mass Transfer, 132, pp. 529–538. https://doi.org/10.1016/j.ijheatmasstransfer.2018.12.033
17. Kim S., Santamarina J.C. (2014). Engineered CO2 injection: The use of surfactants for enhanced sweep efficiency. International Journal of Greenhouse Gas Control, 20, pp. 324–332. https://doi.org/10.1016/j.ijggc.2013.11.018
18. Lu P., Hao Y. Bai Y., Liu W., Chen X., Zheng H., Liu J., Chen Y., Gao J. (2021). Optimal selection of favorable areas for CO2 geological storage in the Majiagou Formation in the Ordos Basin. International Journal of Greenhouse Gas Control, 109, 103360. https://doi.org/10.1016/j.ijggc.2021.103360
19. Mac Dowell N., Fennell P.S., Shah N., Maitland G.C. (2017). The role of CO2 capture and utilization in mitigating climate change. Nature Climate Change, 7, pp. 243–249. https://doi.org/10.1038/nclimate3231
20. Makogon Y.F. (2010). Natural gas hydrates - A promising source of energy. Journal of Natural Gas Science and Engineering, 2, pp. 49–59. https://doi.org/10.1016/j.jngse.2009.12.004
21. Misyura S., Strizhak P., Meleshkin A., Morozov V., Gaidukova O., Shlegel N., Shkola M. (2023). A Review of Gas Capture and Liquid Separation Technologies by CO2 Gas Hydrate. Energies, 16(8), 3318. https://doi.org/10.3390/en16083318
22. Musakaev N.G., Borodin S.L., Gubaidullin A.A. (2020). Methodology for the Numerical Study of the Methane Hydrate Formation During Gas Injection into a Porous Medium. Lobachevskii Journal of Mathematics, 41(7), pp. 1272–1277. https://doi.org/10.1134/S199508022007032X
23. Musakaev N.G., Borodin S.L. (2023). Numerical Study of the Process of Gas Extraction from a Gas Hydrate Reservoir with Inhomogeneous Permeability. Lobachevskii Journal of Mathematics, 44 (5), pp. 1765–1770. https://doi.org/10.1134/S199508022305044X
24. Shagapov V.Sh., Urazov R.R., Musakaev N.G. (2012). Dynamics of formation and dissociation of gas hydrates in pipelines at the various modes of gas transportation. Heat and Mass Transfer, 48 (9), pp. 1589–1600. https://doi.org/10.1007/s00231-012-1000-3
25. Xu G., Schwarz P., Yang H. (2020). Adjusting energy consumption structure to achieve China’s CO2 emissions peak. Renewable and Sustainable Energy Reviews, 122, 109737. https://doi.org/10.1016/j.rser.2020.109737
26. Zhang P., Liu B., Hu L., Meegoda J.N. (2022). Coupled multiphase flow and pore compression computational model for extraction of offshore gas hydrates. Computers and Geotechnics, 145, 104671. https://doi.org/10.1016/j.compgeo.2022.104671
27. Zhou X., Xu Ch., Wen H., Huang Zh., Chuvilin E., Liang D. (2024) Thermal stabilities of CH4 and CO2 hydrates in quartz sands and modeling. Fluid Phase Equilibria, 583, 114120. https://doi.org/10.1016/j.fluid.2024.114120
Об авторах
Н. Г. МусакаевРоссия
Наиль Габсалямович Мусакаев – доктор физ.-мат. наук, профессор, главный научный сотрудник
625026, Тюмень, ул. Таймырская, д. 74
С. Л. Бородин
Россия
Станислав Леонидович Бородин – кандидат физ.-мат. наук, старший научный сотрудник
625026, Тюмень, ул. Таймырская, д. 74
Рецензия
Для цитирования:
Мусакаев Н.Г., Бородин С.Л. Оценка параметров закачки диоксида углерода в насыщенный пористый пласт с неоднородной проницаемостью при наличии гидратообразования. Георесурсы. 2025;27(3):121-129. https://doi.org/10.18599/grs.2025.3.10
For citation:
Musakaev N.G., Borodin S.L. Estimation of the parameters of carbon dioxide injection into a saturated porous reservoir with heterogeneous permeability in the presence of hydrate formation. Georesursy = Georesources. 2025;27(3):121-129. https://doi.org/10.18599/grs.2025.3.10















.png)


