Перейти к:
О методике температурных исследований в буровых скважинах прецизионными термометрами
https://doi.org/10.18599/grs.2024.2.8
Аннотация
Прецизионные автономные скважинные термометры (логгеры) позволяют исследовать температурные аномалии сверхмалой амплитуды (до 1 мK), что значительно расширяет круг задач, которые может решать скважинная термометрия в разведочной геофизике, гидрогеологии, инженерной геологии, геоэкологии и др. При этом методики термокаротажа не развиваются, что не позволяет эффективно реализовать возможности этих приборов. В статье рассмотрены методические вопросы прецизионных температурных измерений в водонаполненных скважинах. Экспериментальные исследования с использованием автономного термометра rBrsolo³ T (RBR Ltd., Канада) показали, что аппаратурный отклик на изменение температуры окружающей среды (релаксация) носит сложный характер. уже через несколько секунд после погружения прибора в скважину он регистрирует температуру, близкую к температуре флюида. однако это временное «окно» достаточно быстро закрывается, и через 15–20 с измеренная температура начинает все больше отличаться от невозмущенной. следующее возвращение измеренной температуры к невозмущенной наступает через 1000–6000 с. Температурная аномалия в интервале 20–600 с осложнена непериодическими колебаниями амплитудой 0,02–0,05 К, связанными с тепловой конвекцией. Наличие временного «окна» на кривой релаксации термометра позволяет быстро и точно измерять температуру флюида в дискретном режиме. с помощью математического моделирования оценены конструктивные параметры термометров, определяющие ширину «окна». Даны рекомендации по проведению прецизионного термокаротажа скважин в непрерывном и дискретном вариантах.
Ключевые слова
Для цитирования:
Демежко Д.Ю., Хацкевич Б.Д., Факаева Н.Р., Горностаева А.А. О методике температурных исследований в буровых скважинах прецизионными термометрами. Георесурсы. 2024;26(2):92–98. https://doi.org/10.18599/grs.2024.2.8
For citation:
Demezhko D.Yu., Khatskevich B.D., Fakaeva N.R., Gornostaeva A.A. On the Method of temperature Measurements in Borehole Using Precision thermometers. Georesursy = Georesources. 2024;26(2):92–98. (In Russ.) https://doi.org/10.18599/grs.2024.2.8
Введение
Температурный каротаж – один из наиболее простых, но в то же время эффективных методов геофизических исследований скважин, широко применяется в нефтяной и промысловой геофизике (Дахнов, 1982; Kutasov, 1999), гидрогеологии (Anderson, 2005; Pehme et al., 2014; Kurylyk et al., 2019), инженерной геологии, геоэкологии, геокриологии (Prensky, 1992), при решении задач глобальной тектоники (Поляк, Хуторской, 2018), палеоклиматологии (Демежко, 2001; Исаев, 2004; Bodri, Cermak, 2007), геодинамики (Shimamura et al., 1984; Демежко и др., 2012; Li et al., 2015). Появление высокоточных автономных температурных логгеров позволяет исследовать процессы, вызывающие температурные аномалии сверхмалой амплитуды (до n·10–3 К), и одновременно исключить негативные факторы, характерные для скважинных термометров на кабеле: задержки сигнала вследствие индуктивности кабеля и шума в коллекторе каротажного подъемника. Однако при этом возникают другие явления, на которые при термокаротаже невысокой точности не обращали внимания, но которые нельзя игнорировать, проводя прецизионные исследования. Во-первых, это инерционность термометров. Требуется некоторое время для достижения датчиком температуры окружающего флюида. В первом приближении, которым обычно и ограничиваются на практике (Costain, 1970; Nielsen, Balling, 1984; Saltus, Clow, 1994), регистрируемая во времени t температура T определяется начальной температурой прибора T1, температурой окружающей среды Т2 и постоянной времени τ:
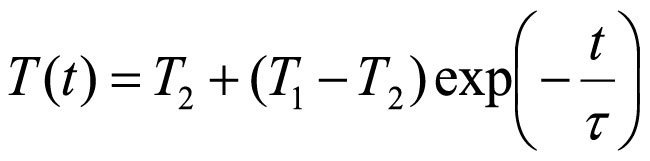 , (1)
, (1)
откуда время, необходимое для достижения требуемой точности ΔT = T(t) – T2, равно
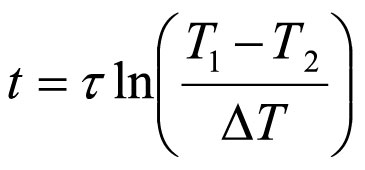 . (2)
. (2)
Так, при разности температур термометра и окружающей среды T1 – T2=1 К и τ = 10 с требуется 23 с для достижения точности 0.1 К и 46 с для достижения точности 0.01 К, при τ = 100 с – 230 и 460 с соответственно. Постоянная времени зависит от тепловой массы прибора, площади его внешней поверхности и коэффициента теплоотдачи. Величину τ определяют экспериментально и за весьма непродолжительное время. Это весьма грубое приближение, пригодное для измерений невысокой точности. Релаксационные зависимости реальных скважинных термометров сложнее, особенно по мере приближения к невозмущенной температуре.
Во-вторых, это свободная тепловая конвекция флюида вблизи датчика. Ее инициируют температурные градиенты, неизбежно возникающие около скважинного прибора, первоначально имеющего отличную от флюида температуру. Нестационарные конвективные течения проявляются в виде температурного шума в записях прибора. По нашим сведениям, это явление ранее не было описано в научной литературе. Хорошо известны температурные эффекты, вызванные свободной тепловой конвекцией в скважине с естественным положительным геотермическим градиентом, превышающим некоторое критическое значение (Gretener, 1967; Diment, 1967; Sammel, 1968; Демежко и др., 2017). Методы, позволяющие устранить или учесть эти эффекты, описаны нами ранее (Демежко и др., 2020, 2021).
В настоящей статье на опыте эксплуатации автономного температурного логгера RBRsolo³ T (RBR Ltd., Канада) и на базе математического моделирования рассмотрены методические аспекты прецизионных температурных исследований в скважинах. Отметим, что установленные закономерности и сделанные выводы не ограничиваются данным прибором и могут быть распространены на другие скважинные приборы.
Скважинный термометр и результаты эксперимента
Автономный температурный логгер RBRsolo³ T (рис. 1) на сегодняшний день обладает наиболее высокими метрологическими характеристиками из всех известных скважинных термометров: погрешность ±0,002 °C, температурное разрешение < 0,00005 °C, постоянная времени в воде ~1 с, стабильность калибровки 0,002 °C/год. Прибор имеет цилиндрический корпус диаметром 25,4 мм и длиной 210 мм, в котором размещены электронные блоки, включая память на 3·107 измерений. Специальный пластик, из которого изготовлен корпус, обеспечивает погружение прибора на глубину до 1700 м. Температурный датчик в тонкой трубке диаметром 2 мм и длиной 25 мм вынесен за пределы корпуса прибора и окружен защитным кожухом с прорезями. Несмотря на то что термометр был разработан в первую очередь для океанографических наблюдений, он широко используется в скважинных исследованиях (Fulton et al., 2013; Li et al., 2015; de La Bernardie et al., 2018; Marcos-Robredo et al., 2022).
Экспериментальные исследования для оценки температурного отклика прибора проводились в обсаженной водонаполненной скважине ИГФ-60, входящей в состав оборудования геотермического полигона Института геофизики УрО РАН (г. Екатеринбург). В течение года верхняя отметка водонаполненного интервала в скважине сохраняется на уровне 7–8 м от поверхности. Предварительно нагретый (до температуры +25 °С) или охлажденный (до –10 °С) термометр быстро опускали на глубину 20 м в воду с температурой около +6 °С. Прибор оставляли в скважине на сутки. Зарегистрированные с дискретностью 1 с изменения температуры T(t) пересчитывали в безразмерные нормализованные температуры:
 (3)
(3)
где T2 – невозмущенная температура, T1 – начальная температура прибора. За начало отсчета времени t = 0 принимался момент касания датчиком воды. Он отмечается максимальной скоростью изменения температуры (рис. 2а). Уже через несколько секунд после погружения в воду прибор регистрирует невозмущенную (на уровне 0,001) температуру, рис. 2б. Однако через 15–20 с измеренная температура начинает все больше отличаться от невозмущенной и вновь возвращается к ней только через 1000–6000 с. Температурная аномалия в интервале 20–600 с осложнена непериодическими колебаниями амплитудой 0,02–0,05, особенно заметными на кривой охлажденного термометра. Столь сложное поведение связано с бо́льшей постоянной времени корпуса прибора по сравнению с постоянной времени вынесенного датчика. Температурная аномалия, создаваемая прибором, достигает датчика лишь через некоторое время после его термализации, и следующий возврат к невозмущенным температурам происходит гораздо медленнее. Практический интерес представляет временно́е «окно», в пределах которого можно быстро и точно измерить невозмущенную температуру. Непериодические вариации обусловлены конвективными течениями флюида, вызываемыми температурными градиентами вблизи корпуса прибора.

Рис. 1. Автономный термометр (логгер) RBRsolo³ T. Фото взято с сайта https://rbr-global.com/products/compact-loggers/rbrsolo-t-2/
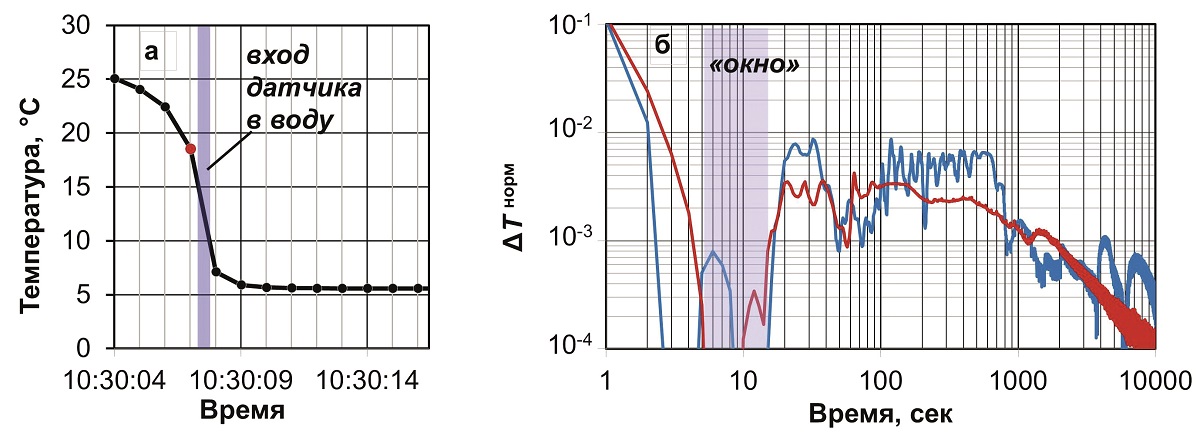
Рис. 2. Релаксационные кривые скважинного термометра RBRsolo³ T: а) изменение температуры предварительно нагретого термометра при погружении в скважину; красная точка отмечает момент перед входом в воду; б) нормализованные температуры; красная кривая – Т1 > T2, синяя – Т1 < T2
Модель
Рассмотрим основные факторы, определяющие ширину «окна». Сам датчик представим в виде тела малых размеров с экспоненциальным температурным откликом (постоянная времени τ1), рис. 3. На расстоянии z от датчика располагается торец корпуса прибора диаметром 2r. И датчик, и корпус прибора первоначально находятся при постоянной температуре Т1. После погружения в воду температура на торце также экспоненциально (с постоянной времени τ2 >> τ1) приближаетcя к невозмущенному значению.
Левые ветви релаксационных кривых на рис. 2б описываются соотношением (1). Предположим, что в момент времени t = 0 температура на торце прибора скачком меняется на небольшую величину D. Распределение температурной аномалии по оси z описывается нестационарным цилиндрически симметричным уравнением теплопроводности (Carslaw, Jaeger, 1958):
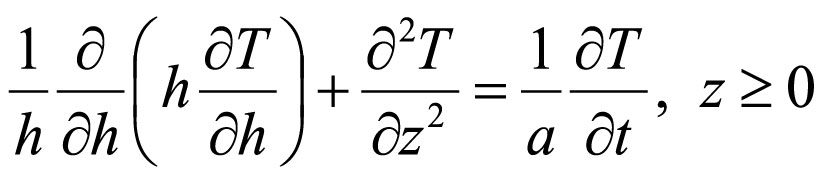 , (4)
, (4)
где T – температура, a – температуропроводность. Решение уравнения (4), удовлетворяющее начальному и граничным условиям:
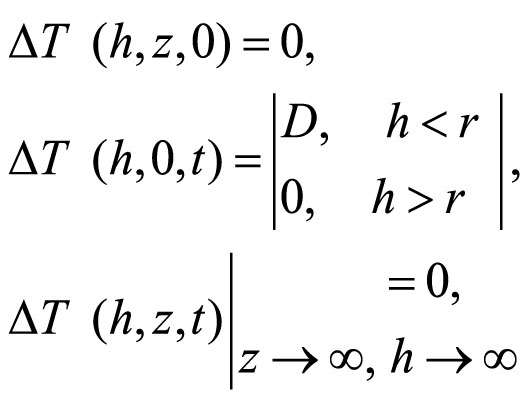 (5)
(5)
на оси симметрии h = 0, получено в (Демежко, 2001):
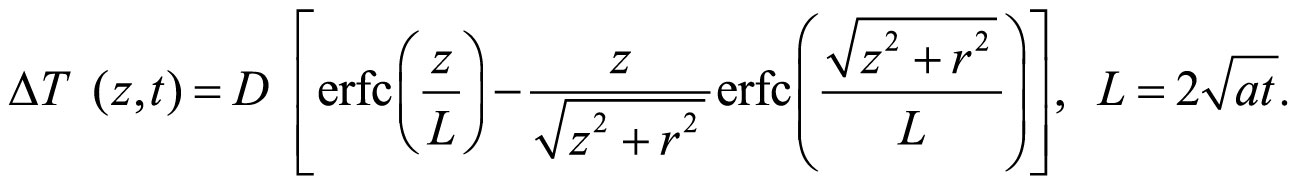 (6)
(6)
Аппроксимируя экспоненциальное изменение температуры торца прибора серией скачков Di:
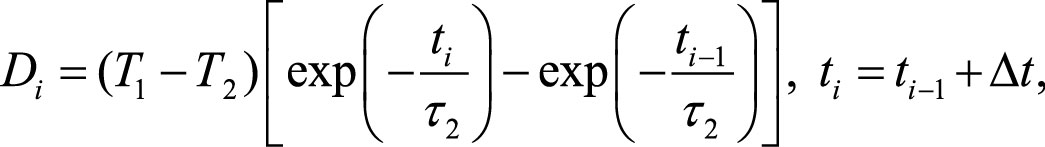 (7)
(7)
получим
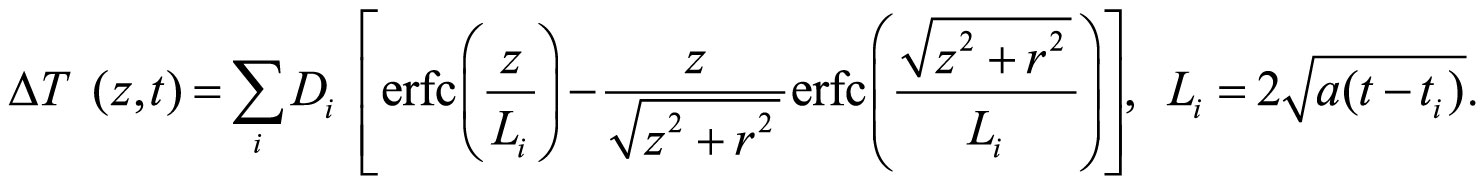 (8)
(8)
Нормализованные в соответствии с (3) зависимости релаксационных кривых от постоянных времени датчика и прибора τ1, τ2, расстояния датчика от корпуса прибора z и диаметра корпуса 2r построены в соответствии с (1) и (7)–(8), представлены на рис. 4.
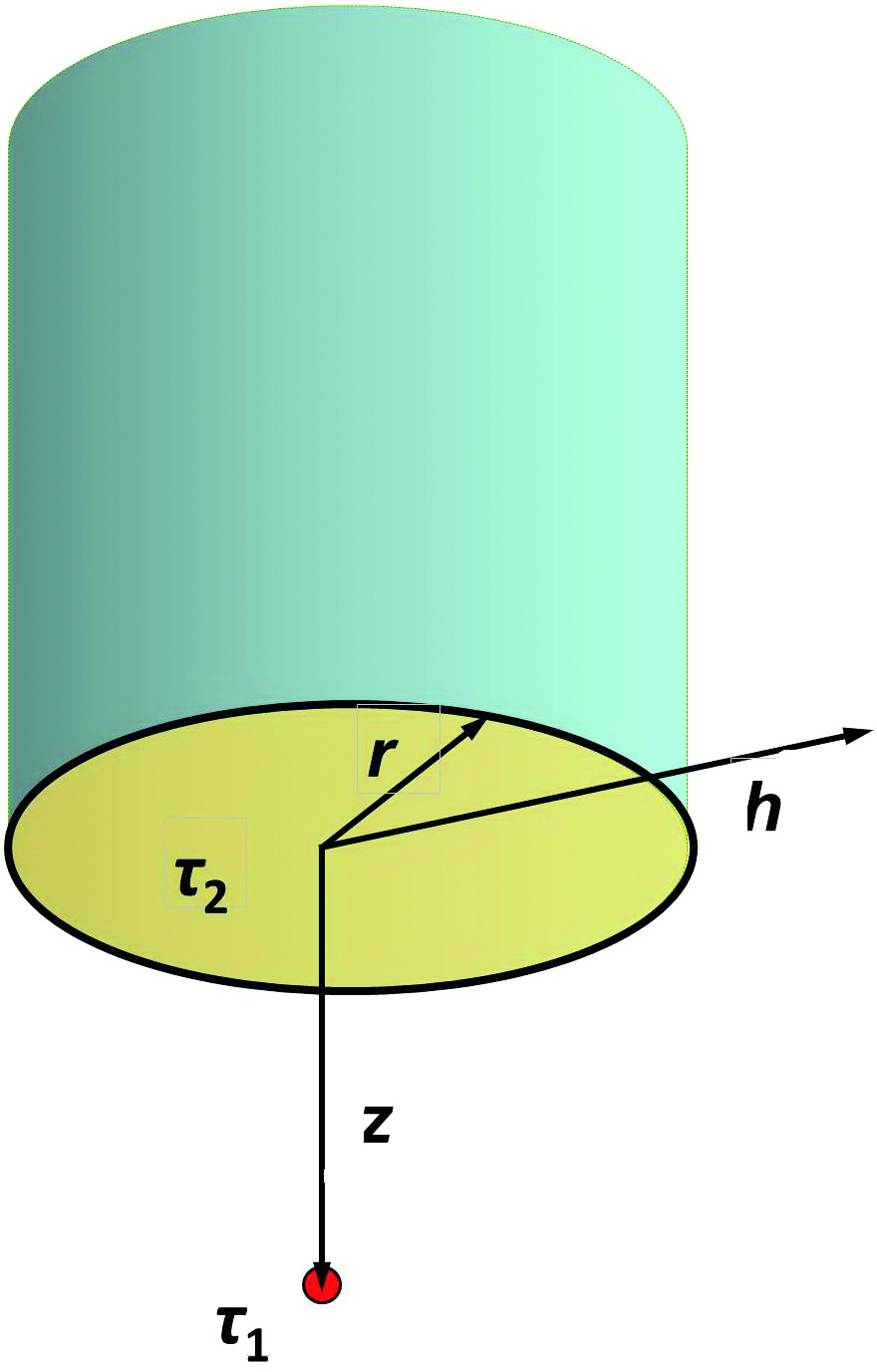
Рис. 3. Условия моделирования. Красной точкой обозначен датчик
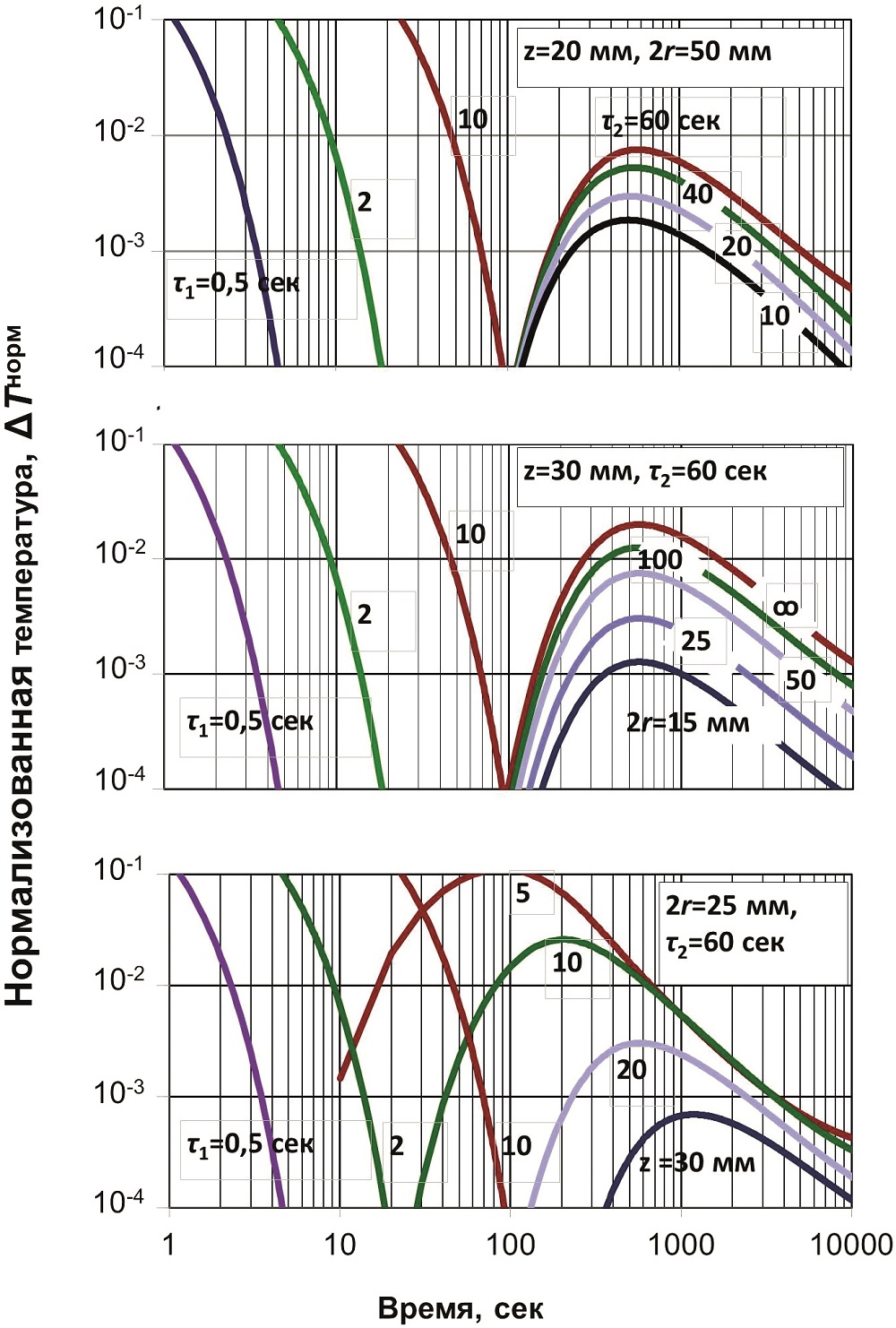
Рис. 4. Теоретические нормализованные релаксационные кривые в зависимости от постоянных времени датчика τ1 и прибора τ2, диаметра прибора 2r и длины датчика z. Температуропроводность воды принималась равной а = 1,37·10–7 м2/с
Обсуждение и рекомендации
Из анализа теоретических релаксационных кривых следует, что наибольшее влияние на ширину измерительного «окна» оказывают длина z и постоянная времени датчика τ1. Увеличение длины выносного датчика является наиболее эффективным способом увеличить ширину «окна». Возможности уменьшения постоянной времени датчика ограничены размерами существующих электронных компонентов – терморезисторов, термисторов, а также необходимостью их защиты от высоких давлений. Уменьшение массы и диаметра скважинного прибора ведет к потере его функциональности и не слишком эффективно. Определенную роль в релаксации играет не учтенный моделью охранный кожух датчика. С этим кожухом, скорее всего, связана первая температурная аномалия экспериментальных кривых на рис. 2б, проявляющаяся несколько раньше, чем предсказывает модель для параметров, близких к параметрам термометра RBRsolo³ T (τ1 = 1 с, τ2 = 60 с, 2r = 25 мм). Более легкий охранный кожух, выполненный, к примеру, из стальной проволоки и отнесенный на максимальное расстояние от датчика, также позволит увеличить измерительное «окно».
Кроме того, температурные аномалии осложнены непериодическими колебаниями (температурным шумом). Эти колебания вызваны свободной тепловой конвекцией, обусловленной температурными градиентами вблизи корпуса прибора. Конвекция в водонаполненной скважине обычно возникает при положительном вертикальном градиенте, когда более теплый (и более легкий) флюид располагается ниже холодного и плотного (Gretener, 1967; Diment, 1967; Sammel, 1968; Демежко и др., 2017). Если скважинный прибор имеет более высокую температуру по сравнению с флюидом, то интенсивная конвекция возникнет вблизи его верхнего окончания. И наоборот, в случае «холодного» прибора интенсивная конвекция возникает внизу, около температурного датчика (рис. 5). В работе (Semin, Levin, 2022) показано, что конвекция может возникнуть и при значительных горизонтальных градиентах. Видимо, влиянием охранного кожуха объясняется конвективный шум, зарегистрированный в пределах первой аномалии.
Очевидно, что наиболее эффективным способом избежать появления конвективного шума уже в начальной части релаксационной кривой является переход от дискретного к непрерывному каротажу.
Температурный каротаж проводится в выстоявшихся скважинах при спуске прибора непрерывно или дискретно. Непрерывный вариант обеспечивает более высокую производительность и позволяет избежать появления температурных аномалий, связанных с охранным кожухом и корпусом прибора. Но в случае применения автономных термометров возникают проблемы привязки по глубине, требующие равномерного спуска и точной синхронизации внутренних часов термометра с работой подъемника. Минимальная скорость каротажа Vмин, очевидно, определяется длиной датчика z и дальней границей измерительного «окна» Δt:
Vмин = z·Δt –1. (9)
Для автономного термометра RBRsolo³ T (z = 0,025 м, Δt = 12 с) получаем Vмин = 7,5 м/ч. Максимальная скорость Vмакс зависит от постоянной времени датчика τ1, геотермического градиента G и допустимой погрешности регистрации температуры ΔT (Reiter et al., 1980):
Vмакс = ΔT·G–1·τ1–1. (10)
Так, при допустимой погрешности ΔT = 0.01 К, геотермическом градиенте G = 0,1 К/м и τ1 = 1 с имеем Vмакс = 360 м/ч. Но для увеличения точности в 10 раз, равно как и при увеличении на порядок температурного градиента, например, в интервале проникновения годовой температурной волны (0–20 м) или в пределах температурной аномалии гидрогеологической природы, потребуется в 10 раз уменьшить скорость каротажа. При невозможности обеспечить необходимую скорость существует способ восстановления реальной температуры по данным, зарегистрированным в ходе непрерывного каротажа инерционными термометрами. Он основан на численном решении уравнения свертки с экспоненциальным ядром относительно подынтегральной функции T(z) (Costain, 1970; Saltus, Clow, 1994; Clow, 2014). Однако решение этой задачи является неустойчивым и требует специальных мер подавления шума.
Дискретный вариант предпочтительно использовать для термокаротажа неглубоких, в первые сотни метров, геотехнических, гидрогеологических, наблюдательных скважин, проводимого с помощью ручной лебедки. В этом случае сложно обеспечить равномерный спуск, кроме того, прибор неоднократно за непродолжительное время извлекается из скважины, подвергаясь воздействию температурных контрастов. В соответствии с выявленным характером релаксации термометра RBRsolo³ T для него можно рекомендовать следующую методику измерений.
- Часы термометра синхронизируются с хронометром оператора с точностью не хуже 1 с и задается частота 1 Гц записи температуры во внутреннюю память.
- Фиксируется время установки на верхней точке водонаполненного интервала скважины.
- Термометр выдерживается на верхней точке 10–15 мин. За это время в значительной степени термализуется корпус прибора.
- На каждой последующей точке термометр выдерживается около 20 с, при этом также фиксируется время остановки. Из полученной записи выбирается один или несколько (с последующим их усреднением) отсчетов, зарегистрированных в пределах «окна», т.е. через 5–12 с после каждой остановки прибора.
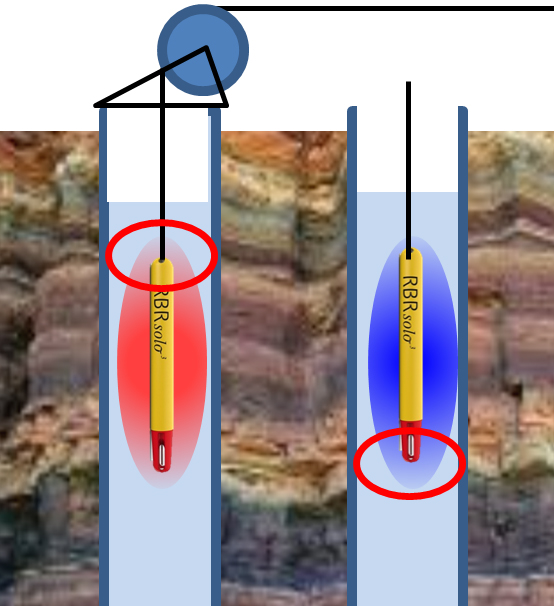
Рис. 5. Схема, поясняющая возникновение свободной тепловой конвекции при остановке «теплого» (Т1 > T2, слева) и «холодного» (Т1 < T2 ) скважинного прибора
Заключение
Несмотря на появление высокоточных автономных скважинных термометров, имеющиеся методики термокаротажа не совершенствуются и не позволяют эффективно использовать потенциал этих приборов. Считается, что отклик прибора на изменение температуры окружающей среды носит монотонный, как правило, экспоненциальный характер. На этом основано распространенное мнение: чем больше время выдержки термометра, тем выше точность измерений. Исследования, проведенные с использованием автономного термометра RBRsolo³ T, показали, что это не соответствует действительности. Наличие «окна», в котором измеряемая температура быстро приближается к невозмущенной, может обеспечить высокую производительность и точность термокаротажа как в непрерывном, так и в дискретном вариантах. Очевидно, что и другие термометры, состоящие из массивного корпуса и вынесенного за его пределы термодатчика, имеют подобный характер релаксации. Применение прецизионных термометров по описанной методике позволит существенно расширить круг задач, решаемых скважинной термометрией, например выделять заколонные перетоки, вызывающие аномалии малой интенсивности, водоносные горизонты в обсаженном интервале гидрогеологической скважины. Повышение точности измерений дает возможность оценивать температурный градиент на коротких интервалах, что, мы надеемся, позволит на новом уровне возродить не применяемый в настоящее время геотермический метод литологического расчленения разреза скважины. Описанные теоретические зависимости ширины «окна» от конструктивных параметров (постоянных времени датчика и прибора, расстояния датчика от корпуса прибора и диаметра корпуса) могут быть полезны разработчикам скважинных термометров.
Список литературы
1. Дахнов В.Н. (1982). Интерпретация результатов геофизических исследований разрезов скважин. М.: Недра, 448 с.
2. Демежко Д.Ю. (2001). Геотермический метод реконструкции палеоклимата (на примере урала). екатеринбург: ИГФ уро рАН, 143 с.
3. Демежко Д.Ю., Миндубаев М.Г., Хацкевич Б.Д. (2017). Температурные эффекты свободной тепловой конвекции в буровых скважинах. Геология и геофизика, 58(10), с. 1602–1610. https://doi.org/10.15372/GiG20171012
4. Демежко Д.Ю., Хацкевич Б.Д, Миндубаев М.Г. (2021). Квазистационарный эффект свободной тепловой конвекции в водонаполненных буровых скважинах. Известия Томского политехнического университета. Инжиниринг георесурсов, 332(7), с. 131–139. https://doi.org/10.18799/24131830/2021/7/3271
5. Демежко Д.Ю., Хацкевич Б.Д., Миндубаев М.Г. (2020). Методы подавления свободной тепловой конвекции в водонаполненных скважинах при проведении температурных исследований. Георесурсы, 22(1), c. 55–62. https://doi.org/10.18599/grs.2020.1.55-62
6. Демежко Д.Ю., Юрков А.К., уткин В.И., Щапов В.А. (2012). Температурные изменения в скважине kun-1 (о. Кунашир), вызванные землетрясением Тохоку (11.03.2011 г., M = 9.0). Доклады Академии наук, 445(2), с. 200–204.
7. Исаев В.И. (2004). Палеотемпературное моделирование осадочного разреза и нефтегазообразование. Тихоокеанская геология, 23(5), с. 101–115. Поляк Б.Г., Хуторской М.Д. (2018). Тепловой поток из недр – индикатор глубинных процессов. Георесурсы, 20(4), Ч. 2, c. 366–376. https://doi.org/10.18599/grs.2018.4.366-376
8. Anderson M.P. (2005). Heat as a ground water tracer. Groundwater, 43(6), pp. 951–968. https://doi.org/10.1111/j.1745-6584.2005.00052.x
9. Bodri L., Cermak V. (2007). Borehole climatology: A new method how to reconstruct climate. Elsevier. 352 p. https://doi.org/10.1016/B978-0-08045320-0.X5000-5
10. Carslaw H., Jaeger J.C. (1958). Conduction of heat in soils. Clarendon Press, Oxford. 510 p.
11. Clow G.D. (2014). Temperature data acquired from the DOI/GTN-P Deep Borehole Array on the Arctic Slope of Alaska, 1973–2013. Earth System Science Data, 6(1), pp. 201–218. https://doi.org/10.5194/essd-6-201-2014
12. Costain J.K. (1970). Probe response and continuous temperature measurements. Journal of Geophysical Research, 75(20), pp. 3969–3975. https://doi.org/10.1029/JB075i020p03967
13. de La Bernardie J., Bour O., Le Borgne T., Guihéneuf N., Chatton E., Labasque T., Le Lay H., Gerard M.F. (2018). Thermal attenuation and lag time in fractured rock: Theory and field measurements from joint heat and solute tracer tests. Water Resources Research, 54(12), pp. 10053–10075. https://doi.org/10.1029/2018WR023199
14. Diment W.H. (1967). Thermal regime of a large diameter borehole: Instability of the water column and comparison of airand water-filled conditions. Geophysics, 32(4), pp. 720–726. https://doi.org/10.1190/1.1439885
15. Fulton P.M., Brodsky E.E., Kano Y., Mori J., Chester F., Ishikawa T., Harris R.N., Lin W., Eguchi N., Toczko S., and Expedition 343, 343T, and KR13-08 Scientists. (2013). Low coseismic friction on the Tohoku-Oki fault determined from temperature measurements. Science, 342(6163), pp. 1214–1217. https://doi.org/10.1126/science.1243641
16. Gretener P.E. (1967). On the thermal instability of large diameter wells – an observational report. Geophysics, 32(4), pp. 583–787. https://doi.org/10.1190/1.1439886
17. Kurylyk B.L., Irvine D.J., Bense V.F. (2019). Theory, tools, and multidisciplinary applications for tracing groundwater fluxes from temperature profiles. WIREs Water, 6(1), e1329. https://doi.org/10.1002/wat2.1329
18. Kutasov I.M. (1999). Applied geothermics for petroleum engineers. Elsevier, 346 p.
19. Li H., Xue L., Brodsky E.E., Mori J.J., Fulton P.M., Wang H., Kano Y., Yun K., Harris R.N., Gong Z., Li C. (2015). Long-term temperature records following the Mw 7.9 Wenchuan (China) earthquake are consistent with low friction. Geology, 43(2), pp. 163–166. https://doi.org/10.1130/G35515.1
20. Marcos-Robredo G., Rey-Ronco M.Á., Castro-García M.P., AlonsoSánchez T. (2022). A Device to Register Temperature in Boreholes in Northwest Spain for Geothermal Research. Sensors, 22(13), 4945. https:// doi.org/10.3390/s22134945
21. Nielsen S.B., Balling N. (1984). Accuracy and resolution in continuous temperature logging. Tectonophysics, 103(1–4), pp. 1–10. https://doi.org/10.1016/0040-1951(84)90069-6
22. Pehme P., Parker B.L., Cherry J.A., Blohm D. (2014). Detailed measurement of the magnitude and orientation of thermal gradients in lined boreholes for characterizing groundwater flow in fractured rock. Journal of Hydrology, 513, pp. 101–114. https://doi.org/10.1016/j.jhydrol.2014.03.015
23. Prensky S. (1992). Temperature measurements in boreholes – An overview of engineering and scientific applications. The Log Analyst, 33(3), pp. 313–333.
24. Reiter M., Mansure A.J., Peterson B.K. (1980). Precision continuous temperature logging and comparison with other types of logs. Geophysics, 45(12), pp. 1857–1868. https://doi.org/10.1190/1.1441070
25. Saltus R.W., Clow G.D. (1994). Deconvolution of continuous borehole temperature logs: Example from the Greenland GISP2 icecore hole. Department of the Interior. U.S. Geological Survey Open-File Report, 94–254, 42 p. https://pubs.usgs.gov/of/1994/0254/report.pdf
26. Sammel E.A. (1968). Convective flow and its effect on temperature logging in small-diameter wells. Geophysics, 33(6), pp. 1004–1012. https://doi.org/10.1190/1.1439977
27. Semin M., Levin L. (2022). Study of the Influence of Thermal Convection on Temperature Measurement in Thermal Control Boreholes during Artificial Ground Freezing. Fluids, 7(9), 298. https://doi.org/10.3390/fluids7090298
28. Shimamura H., Ino M., Hikawa H., Iwasaki T. (1984). Groundwater microtemperature in earthquake regions. Pure and Applied Geophysics, 122(6), pp. 933–946. https://doi.org/10.1007/BF00876394
Об авторах
Д. Ю. ДемежкоРоссия
Дмитрий Юрьевич Демежко – доктор геол.-минерал. наук, главный научный сотрудник лаборатории геодинамики
620016, Екатеринбург, ул. Амундсена, д. 100
Б. Д. Хацкевич
Россия
Богдан Дмитриевич Хацкевич – научный сотрудник лаборатории геодинамики
620016, Екатеринбург, ул. Амундсена, д. 100
Н. Р. Факаева
Россия
Нелли Рафаэлевна Факаева – младший научный сотрудник лаборатории геодинамики
620016, Екатеринбург, ул. Амундсена, д. 100
А. А. Горностаева
Россия
Анастасия Александровна Горностаева – кандидат физ.-мат. наук, старший научный сотрудник лаборатории геодинамики
620016, Екатеринбург, ул. Амундсена, д. 100
Рецензия
Для цитирования:
Демежко Д.Ю., Хацкевич Б.Д., Факаева Н.Р., Горностаева А.А. О методике температурных исследований в буровых скважинах прецизионными термометрами. Георесурсы. 2024;26(2):92–98. https://doi.org/10.18599/grs.2024.2.8
For citation:
Demezhko D.Yu., Khatskevich B.D., Fakaeva N.R., Gornostaeva A.A. On the Method of temperature Measurements in Borehole Using Precision thermometers. Georesursy = Georesources. 2024;26(2):92–98. (In Russ.) https://doi.org/10.18599/grs.2024.2.8















.png)


