Перейти к:
Применение статистических методов оценки трещиноватых коллекторов по промысловым данным
https://doi.org/10.18599/grs.2025.1.3
Аннотация
В трещиноватых коллекторах наличие трещин может оказывать как негативное, так и положительное влияние на технико-экономические показатели разработки месторождения, поэтому важным условием является ранняя классификация трещин. Идентификация типа трещиноватого коллектора на начальных стадиях разработки является ключом к подбору оптимального типа модели и системы разработки месторождения. В статье проведена оценка применимости показателя накопленной добычи и коэффициента продуктивности по скважинам для определения типа трещиноватого коллектора с использованием статистического метода анализа кривой Лоренца и коэффициента Джини (в применении к определению влияния трещин) при небольших выборках данных и на начальных стадиях разработки. Для исследования коэффициента влияния трещин при небольшом фонде скважин в статье использован метод математической статистики – бутстреп-метод. Этот метод основан на многократной генерации множества случайных выборок из исходных данных и на их последующем статистическом анализе. Моделирование выборок проводилось при помощи генератора случайных чисел в электронных таблицах. По результатам исследований установлено, что применение для идентификации трещиноватых коллекторов при небольшом количестве скважин таких показателей, как накопленная добыча и коэффициент продуктивности, показало сопоставимые результаты. Для повышения достоверности классификации при небольшом количестве скважин требуется выборка данных, которая будет наиболее полно описывать месторождение. Получить представительную выборку данных для объективного анализа распределения и влияния систем трещин возможно размещением скважин с охватом всей площади месторождения. На ранних стадиях разработки из-за незначительных объемов добываемой продукции и небольших сроков работы скважин для анализа рекомендовано использовать коэффициент продуктивности.
Ключевые слова
Для цитирования:
Щекин А.И. Применение статистических методов оценки трещиноватых коллекторов по промысловым данным. Георесурсы. 2025;27(1):275-283. https://doi.org/10.18599/grs.2025.1.3
For citation:
Shchekin A.I. Applying Statistical Methods to Assess Fractured Reservoirs Relying on Field Data. Georesursy = Georesources. 2025;27(1):275-283. (In Russ.) https://doi.org/10.18599/grs.2025.1.3
Введение
В последнее время в мире отмечается растущее внимание многих исследователей к роли трещин при разработке месторождений углеводородов. Повышенный интерес к трещиноватым коллекторам вызван прежде всего увеличением числа месторождений и проектов по увеличению нефтеотдачи в сложных коллекторах с естественной трещиноватостью, часто представленных карбонатными (Spence et al., 2014; Manrique et al., 2010). Высокая неопределенность при исследовании распределения трещинных систем в объеме породы-коллектора и сложность прогнозирования поведения пласта при его разработке являются причинами снижения коэффициента извлечения нефти или газа. Трещиноватость коллектора – это основной параметр, определяющий распределение фильтрационно-емкостных свойств (ФЕС), от степени изучения которого зависит успешность разработки того или иного месторождения (Bourbiaux, 2010; Narr et al., 2006). Для точной оценки параметров трещин в скважинах разработан и применяется широкий спектр геофизических, петрофизических и инженерных методов (Lorenz, Cooper, 2020).
Одними из первых исследований, в которых подчеркнута целесообразность рассмотрения трещиноватых коллекторов как отдельной самостоятельной категории, были работы (Aguilera, 1995) и (Nelson, 1985). На тот момент они обобщили имеющийся объем исследований и опыт разработки месторождений в трещиноватых коллекторах, что позволило заложить основу для дальнейшего развития данного научного направления.
Последующие тематические работы посвящены различным аспектам теоретического и прикладного характера изучения трещиноватых пород. Так, в статье (Baker, Kuppe, 2000) предложена методология объединения «прямого» и «обратного» подхода по исследованию трещинного пустотного пространства, характеристики матрицы и трещин и параметров их взаимодействия. Прямой подход направлен на изучение различных причин происхождения естественных трещин и их свойств (геологические, геофизические и петрофизические исследования), тогда как обратный подход заключается в оценке отклика (эффекта), создаваемого при разработке месторождения (история добычи, гидродинамические, трассерные исследования и др.). В обзоре (Spence et al., 2014) обобщены основные достижения, связанные с развитием интегрированных междисциплинарных подходов по изучению трещиноватых коллекторов. Внедрение подобного подхода по изучению трещиноватых коллекторов, как считают авторы работы (Spence et al., 2014), прежде всего обусловлено снижением неопределенности и максимизацией извлечения углеводородов и должно быть направлено на повышение точности количественной оценки сети трещин и использования этих данных для построения моделей. В целом в научных работах подчеркивается важность и актуальность объединения усилий ученых из различных областей для изучения особенностей, присущих трещиноватым коллекторам.
Результаты оценки распределения систем трещин и степени их влияния на ФЕС или движение флюидов позволили разработать различные критерии, применяемые для классификации трещиноватых коллекторов. При этом существует два основных направления в идентификации трещиноватых коллекторов: первое ориентировано на типизацию трещиноватых коллекторов по результатам изучения свойств трещин по данным геолого-геофизических и петрофизических методов, второе – на оценку степени вклада трещин и матрицы в разработку месторождения и работу скважин (инженерные или промысловые классификации). Предварительная диагностика типа трещиноватого коллектора по анализу параметров разработки скважин позволяет обоснованно определить оптимальную стратегию освоения месторождения. Целью данной статьи является исследование проблем идентификации трещиноватых коллекторов и оценки влияния трещин по промысловым данным при небольшом количестве скважин и на ранних стадиях разработки с применением статистических методов.
Особенности классификации трещиноватых коллекторов по промысловым данным
Наиболее распространенную промысловую классификацию трещиноватых коллекторов представил Нельсон (Nelson, 2001), где в качестве первоначальной концепции были использованы принципы разделения трещиноватых коллекторов, предложенные Хаббертом и Уиллисом (Nelson, 2020). Ими были выделены только две группы трещиноватых коллекторов: в одной трещины обеспечивают и пористость, и проницаемость коллектора, во второй трещины обеспечивают проницаемость, а матрица – пористость. Основная идея детализированной классификации Нельсона для трещиноватого коллектора состоит не в том, чтобы идентифицировать и присвоить тип коллектора, а в том, чтобы оценить степень влияния трещин на процесс извлечения углеводородов. В работах (Nelson, 2001; Baker, Kuppe, 2000; Tiab, Donaldson, 2015; Ahr, 2011) представлены основные характеристики типов трещиноватых коллекторов, их диагностические признаки и потенциальные проблемы, которые могут наблюдаться при разработке коллекторов того или иного типа. При таком подходе на основе изучения подобных месторождений идентификация типа трещиноватых коллекторов позволяет осуществить подбор оптимальной стратегии освоения месторождений с учетом влияния трещиноватости.
В усовершенствованной классификации Нельсона выделяют четыре типа трещиноватых коллекторов (Nelson, 2001; Щекин и др., 2021):
- тип I – трещины обеспечивают основную пористость и проницаемость коллектора, матрица характеризуется низкими значениями пористости и проницаемости;
- тип II – трещины обеспечивают основную проницаемость коллектора, а матрица – основную пористость, которая может изменяться в широком диапазоне;
- тип III – трещины дополняют проницаемость коллектора и повышают экономическую рентабельность разработки коллектора, который в целом характеризуется хорошими значениями пористости и проницаемости;
- тип IV – трещины не обеспечивают дополнительной пористости и проницаемости, но формируют значительную анизотропию коллектора (барьеры для потока).
На рис. 1 представлена графическая визуализация выделенных типов трещиноватых коллекторов с указанием положения каждого типа в процентах от общей пористости и процента от общей проницаемости. Если первые три типа трещиноватого коллектора описывают положительные коллекторские свойства системы трещин, то последний тип введен для описания влияния трещин на анизотропию коллекторских свойств.

Рис. 1. Схематическое распределение трещиноватых коллекторов по типам (Nelson, 2020). Обозначения: kf – проницаемость трещин, km – проницаемость матрицы, ϕf – пористость (пустотность) трещин, ϕm – пористость матрицы, I, II, III, IV – типы трещиноватых коллекторов.
Одно из основных преимуществ применения подобных промысловых классификаций по определению типа трещиноватого коллектора заключается в возможности подбора концепции моделирования и разработки объекта с учетом влияния трещинных систем. В работе (Nelson, 2020) представлены рекомендации по предпочтительному виду геолого-гидродинамической модели для конкретных типов трещиноватого коллектора. По мнению автора (Nelson, 2020), это позволит повысить точность прогнозирования запасов и степени их извлечения при правильным задании трещин в модели. Например, для первого типа трещиноватых коллекторов рекомендуется применять модель одинарной пористости, что позволит смоделировать фильтрацию только при наличии одной среды, в данном случае трещин. Для второго типа трещиноватого коллектора, где необходимо учесть наличие матрицы, рекомендуется модель двойной пористости. Наиболее сложным строением с точки зрения моделирования фильтрации являются коллектора третьего типа, когда необходимо учитывать ФЕС и матрицы, и трещин, в том числе их взаимодействие. В таком случае автором (Nelson, 2020) наряду с вышеперечисленными моделями предлагается также рассматривать модель двойной пористости и двойной проницаемости. В свою очередь, как отмечается в работе (Закревский, Кундин, 2016), классифицирование сложных коллекторов также может быть связано с созданием концептуальной модели трещинообразования. В целом необходимость комплексного изучения трещиноватых коллекторов прежде всего направлена на повышение точности количественной оценки распределения систем трещин в объеме резервуара и использование этих данных для построения моделей.
На базе этой классификации опубликованы научные работы (Allan, Sun, 2003; Sun, Sloan, 2003) с обобщением истории разработки месторождений в трещиноватых коллекторах. Авторами выполнен анализ влияния на коэффициент нефтеизвлечения различных свойств коллекторов и флюидов, систем трещин, а также вида режимов разработки месторождений по типам трещиноватых коллекторов. Как показывают результаты анализа, прогнозирование показателей разработки и конечных величин извлечения нефти в трещиноватых коллекторах характеризуется высокой неопределенностью, и, как следствие, это может привести к проблемам при разработке коллектора. Подобные исследования опыта разработки месторождений углеводородов в трещиноватых коллекторах дают возможность сформировать базу «лучших практик» для дальнейшего применения в качестве аналогов на более сложных по геологическому строению объектах.
Основным недостатком классификации Нельсона является отсутствие понятных критериев по выделению коллекторов определенного типа. Так, в работе (Nelson, 2001) для идентификации типа трещиноватого коллектора предложено использовать статистический анализ параметров разработки месторождений, в частности, накопленной добычи нефти. Статистический метод на основе кривой Лоренца, как правило, демонстрирует резкое отличие в параметрах работы скважин в результате неоднородного распределения трещин, в данном случае в значениях накопленной добычи (рис. 2). Как известно, при построении кривой Лоренца по оси абсцисс отображается накопленный процент количества анализируемых скважин, упорядоченных по возрастанию накопленной добычи, по оси ординат – процент от общей накопленной добычи нефти, т.е. их вклад в общую добычу. Линия, проведенная под углом 45 градусов, является линией однородного коллектора, если кривая отдаляется от линии однородного коллектора в сторону абсцисс, то возрастает неравномерность в распределении накопленной добычи по скважинам. Трещиноватые коллектора характеризуются наибольшим отклонением кривой, матричные – наименьшим, приближаясь к прямой линии. На рис. 2 показаны кривые Лоренца и границы типов трещиноватых коллекторов. Дополнительно на график нанесены примеры месторождений из РФ и других стран, с характерным трещиноватым строением коллектора (Мартюшев, 2014; Akhkubekov, Vasilyev, 2010; Toledo-Piña et al., 2014; Marchal et al., 2005). Красная пунктирная линия указывает 50% накопленную добычу по скважинам, т.е. пересечение кривой конкретного месторождений с этой линией отражает то количество скважин, к которым приурочен остальной 50% объем накопленной добычи нефти. Таким образом, в основе данного подхода лежит предположение, что основной объем добычи приходится на небольшое количество скважин, расположенных в высокопродуктивных зонах, как правило, вскрывающих системы трещин.

Рис. 2. Кривые Лоренца и границы типов трещиноватых коллекторов
Оценка степени влияния трещинной неоднородности по кривой Лоренца сопровождается определением коэффициента Джини или коэффициента влияния трещин. Коэффициент влияния трещин принимает значения от 0 (для однородного коллектора) до 1. Увеличение значения данного коэффициента указывает на существенное влияние системы трещин на распределение объемов добываемых углеводородов по скважинам. В работе (Щекин и др., 2021) авторами были представлены примерные диапазоны изменения коэффициента влияния трещин по типам трещиноватых коллекторов:
- I тип – более 0,7;
- II тип – 0,5–0,7;
- III тип – 0,2–0,5;
- IV тип – менее 0,2.
В других тематических исследованиях для идентификации типа коллектора по Нельсону исследователи определяют численное соотношение коэффициентов проницаемости и пористости матрицы и трещин (рис. 1), либо используют производные их показатели.
Авторы научного исследования (Sun, Pollitt, 2021) отмечают ряд недостатков существующих классификаций трещиноватых коллекторов, в том числе и классификации Нельсона:
- классификация Нельсона сосредоточена на изучении параметров трещин с точки зрения их емкости и проницаемости, не учитывая при этом свойства матрицы, которая часто оказывает не меньшее влияние на продуктивность пласта;
- разницу между II и III типами можно субъективно определить только по данным показателей экономической рентабельности месторождения.
Как считают авторы работы (Sun, Pollitt, 2021), хотя трещинная проницаемость и имеет решающее значение для определения типа трещиноватых коллекторов, именно параметры матрицы будут определять их основные свойства. На основе изучения истории разработки более чем 310 объектов и с учетом вышеприведенных недостатков классификации Нельсона, авторами (Sun, Pollitt, 2021) предложен несколько иной подход к выделению типов трещиноватых коллекторов на основе классификации матрицы: тип I (плотная матрица), тип II (макропористая матрица) и тип III (микропористая матрица). Следует отметить, что для разделения II-го и III-го типов коллектора предложен численный критерий – размер пор, который составляет для II-го типа более 20 мкм, для III-го типа – менее 20 мкм.
Проблемы идентификации трещиноватых коллекторов по промысловым данным
Многими исследователями подчеркивается необходимость классификации и идентификации типа трещиноватого коллектора. Наличие трещин может оказать как негативное, так и положительное влияние на технико-экономические показатели разработки месторождения, поэтому важным условием является ранняя оценка степени влияния трещин. Диагностика трещин и идентификация типа трещиноватого коллектора на начальных стадиях разработки является ключом к подбору оптимального типа модели и системы разработки.
Как было показано выше, основным показателем для построения диаграммы Лоренца и выделения типа трещиноватого коллектора с определением коэффициента влияния трещин (Nelson, 2001) является накопленная добыча по скважинам. Проведем оценку применимости показателя накопленной добычи по скважинам для определения типа трещиноватого коллектора с использованием статистического метода анализа кривой Лоренца и коэффициента Джини (коэффициента влияния трещин) при небольших выборках данных и на начальных стадиях разработки. На рис. 3 представлена динамика коэффициента влияния трещин с начала разработки, рассчитанного по значениям накопленной добычи нефти, на примере фундамента месторождения Белый тигр, в частности, центрального блока (Щекин и др., 2021). Как видно, с увеличением фонда скважин и накопленной добычи коэффициент влияния трещиноватости резко возрастает и достигает более-менее объективных значений через 8 лет с начала разработки. Дальнейший равномерный рост коэффициента влияния трещин на протяжении разработки характеризует вовлечение краевых зон с более низкими значениями ФЕС. Эти данные объясняются увеличением доли низкодебитных скважин в низкопродуктивных зонах к концу разработки и соответственно повышением степени влияния неоднородности. Недостаточные и неравномерные объемы добычи нефти по скважинам предопределяют низкую достоверность при оценке коэффициента влияния трещин с построением кривой Лоренца на ранних стадиях разработки. Основываясь на этом, исследование влияния трещинных систем на параметры работы скважин и, соответственно, идентификация типа коллектора возможна на месторождениях с довольно длительным периодом разработки.
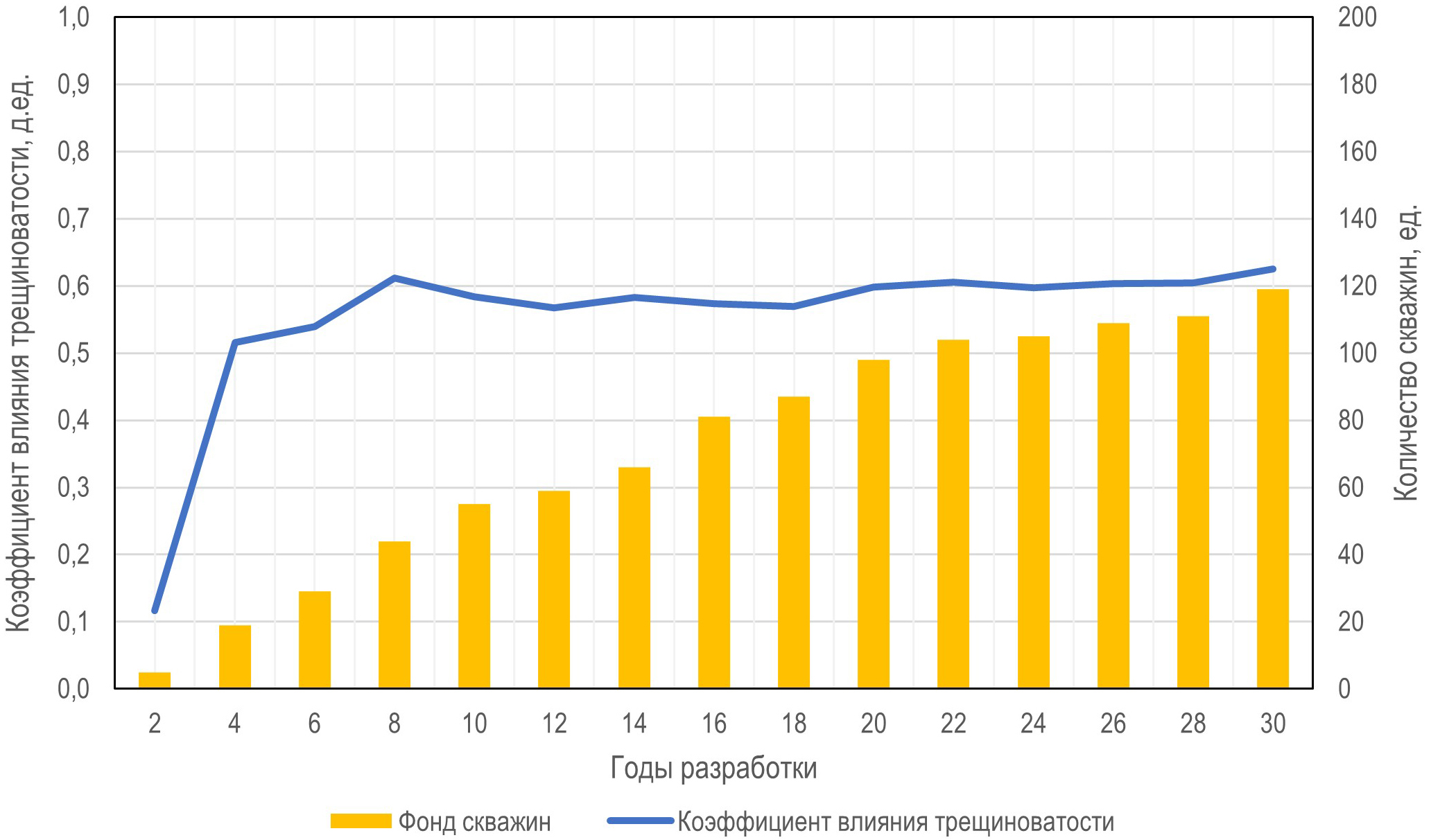
Рис. 3. Динамика коэффициента влияния трещин G с начала разработки, рассчитанного по значениям накопленной добычи нефти
Согласно (Щекин и др., 2021), использование таких показателей, как накопленная добыча и максимальный дебит по скважинам, не может объективно отражать распределение трещинной неоднородности по коллекторам. В целом, на величину накопленной добычи нефти по скважинам оказывает влияние ряд факторов, таких как: внедрение методов увеличения нефтеотдачи, преждевременное обводнение, сроки ввода и выбытия скважин, проведение геолого-технических мероприятий и т.п. В работе (Щекин и др., 2021) для корректного анализа и объективной оценки влияния трещинной неоднородности предложено пользоваться таким параметром, как коэффициент продуктивности. Коэффициент продуктивности характеризует фильтрационные свойства пласта и влияние систем трещин, вскрытых скважиной, и по сравнению с накопленной добычей может быть получен по скважинам в начальные периоды разработки. На рис. 4 представлена динамика коэффициента влияний трещин по годам, рассчитанная на основе данных по коэффициенту продуктивности. Как видно из анализа рисунка, динамика коэффициента влияния трещин, в данном случае, имеет существенно иную картину, чем рассмотренная ранее. Коэффициент влияния трещин по коэффициенту продуктивности на первый год разработки при 5 скважинах составляет 0,584 и характеризуется тенденцией к росту с увеличением фонда скважин и охватом разбуриваемой площади месторождения, достигая значения 0,744 д.е. на конец анализируемого периода.
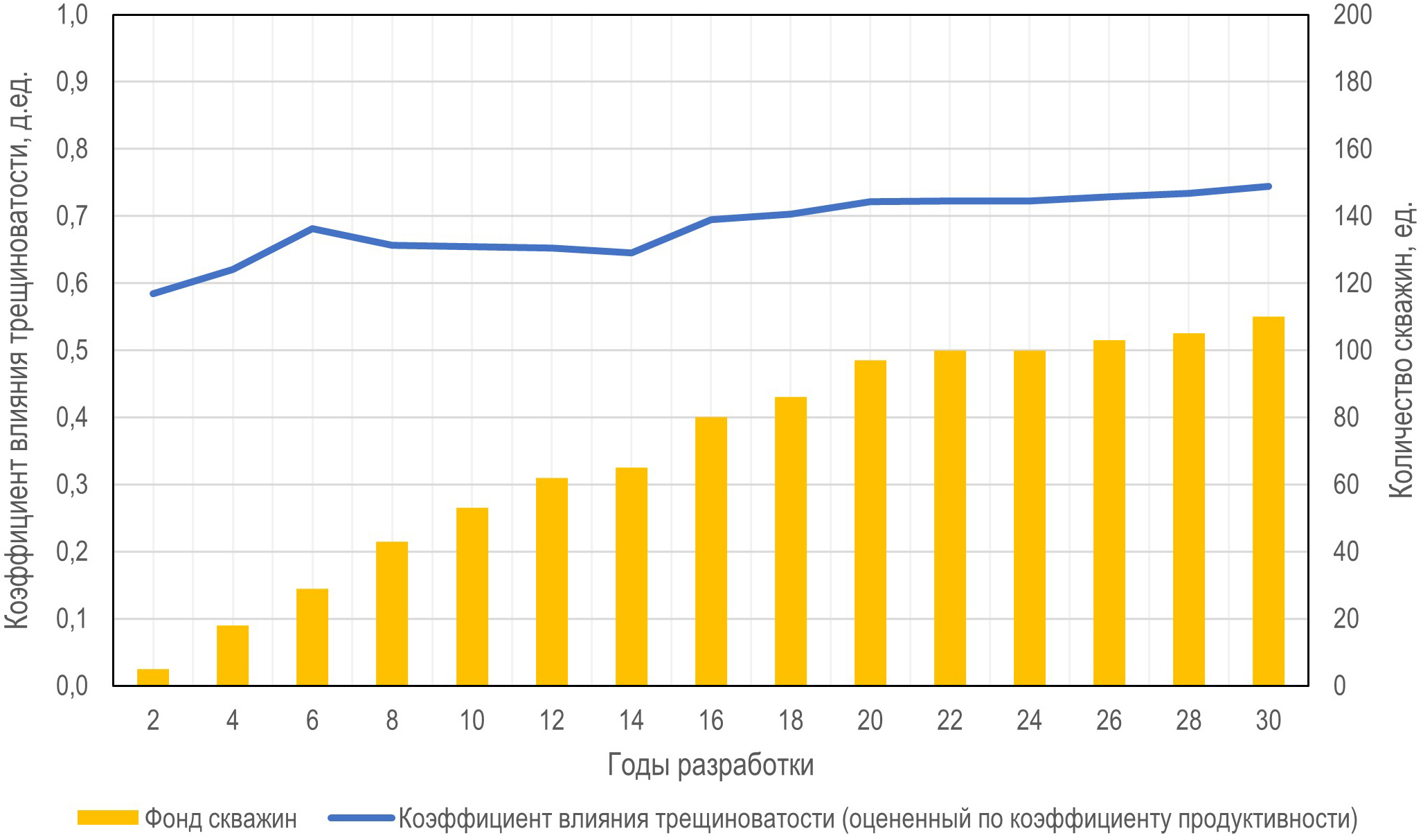
Рис. 4. Динамика коэффициента влияний трещин GPI по годам, рассчитанная на основе распределения коэффициента продуктивности
Таким образом, с одной стороны, низкие значения коэффициента влияния трещин можно объяснить недостаточной историей разработки и, соответственно, накопленной добычи нефти за рассматриваемый период, с другой стороны, – недостаточным количеством скважин для анализа. И если определение типа трещиноватого коллектора путем анализа накопленной добычи может решаться по мере накопления промысловых данных, то в случае залежей, находящихся на ранних стадиях разработки, с малочисленным фондом скважин, доступным для анализа, расчет коэффициента влияния трещин все еще остается нерешенной проблемой.
Результаты исследования применимости статистических методов оценки трещиноватых коллекторов при небольшом фонде скважин
Для исследования коэффициента Джини (коэффициента влияния трещин в рассматриваемом контексте) при малых выборках применяется один из методов математической статистики – бутстреп метод (Yitzhaki, Schechtman, 2013). Суть метода заключается в многократной генерации из исходного набора данных множества случайных выборок с возвратом того же размера, что и исходный набор данных с последующей статистической обработкой сгенерированных выборок.
Обсуждение и обоснование возможности использования указанного метода при расчете коэффициента Джини для выборок малого размера приведено в (Dixon et al., 1987). Согласно (Dixon et al., 1987), по результатам бутстрепинга по каждой сгенерированной выборке определяются значения коэффициента Джини, которые далее используются для расчета и анализа доверительных интервалов этого коэффициента. При этом, если для каждого набора сгенерированных выборок данных из всей популяции рассчитан доверительный интервал, то многократно повторяя процесс генерации выборок, можно определить количество доверительных интервалов, включающих истинное значение коэффициента Джини всей популяции.
При помощи бутстрепинга проведена оценка применимости кривой Лоренца и коэффициента влияния трещин при небольшом количестве скважин. Моделирование проводилось при помощи генератора случайных чисел в электронных таблицах (Mélard, 2014). Состоятельность метода оценивалась попаданием известного коэффициента влияния трещин начальной выборки, содержащей полный набор данных, в рассчитанные доверительные интервалы по сгенерированным случайным выборкам малого объема. Для расчета коэффициента Джини использовалась классическая формула:
![]()
где ![]() – среднее значение, при этом для обеспечения несмещенности рассчитанное значение коэффициента G дополнительно умножалось на поправку n/(n – 1), как это, в частности, сделано в (Dixon et al., 1987).
– среднее значение, при этом для обеспечения несмещенности рассчитанное значение коэффициента G дополнительно умножалось на поправку n/(n – 1), как это, в частности, сделано в (Dixon et al., 1987).
Для исследования была использована исходная выборка скважин с накопленной добычей за более чем 20-летний период разработки месторождения в трещиноватых коллекторах (Щекин и др., 2021). Значение коэффициента влияния трещин по исходной выборке составляет G = 0,625. После ранжирования скважин исходной совокупности от меньшего к большему значению по накопленной добыче выполнено создание интервальной выборки путем регулярного отбора каждой шестой скважины из исходного списка. Такой подход позволяет увеличить границы формируемой совокупности данных. Интервальная выборка включает 20 скважин с накопленной добычей, такой же, как и в начальной выборке. Коэффициент влияния трещин интервальной совокупности скважин составляет G = 0,634, что характеризует достаточно близкие значения сравниваемых выборок при сокращении количества скважин. В данном случае интервальная выборка является репрезентативной.
Далее с применением метода бутстрепинга выполнена серия расчетов с генерацией случайных выборок на основе исходной и интервальной совокупностей данных. Результаты моделирования представлены в табл. 1.
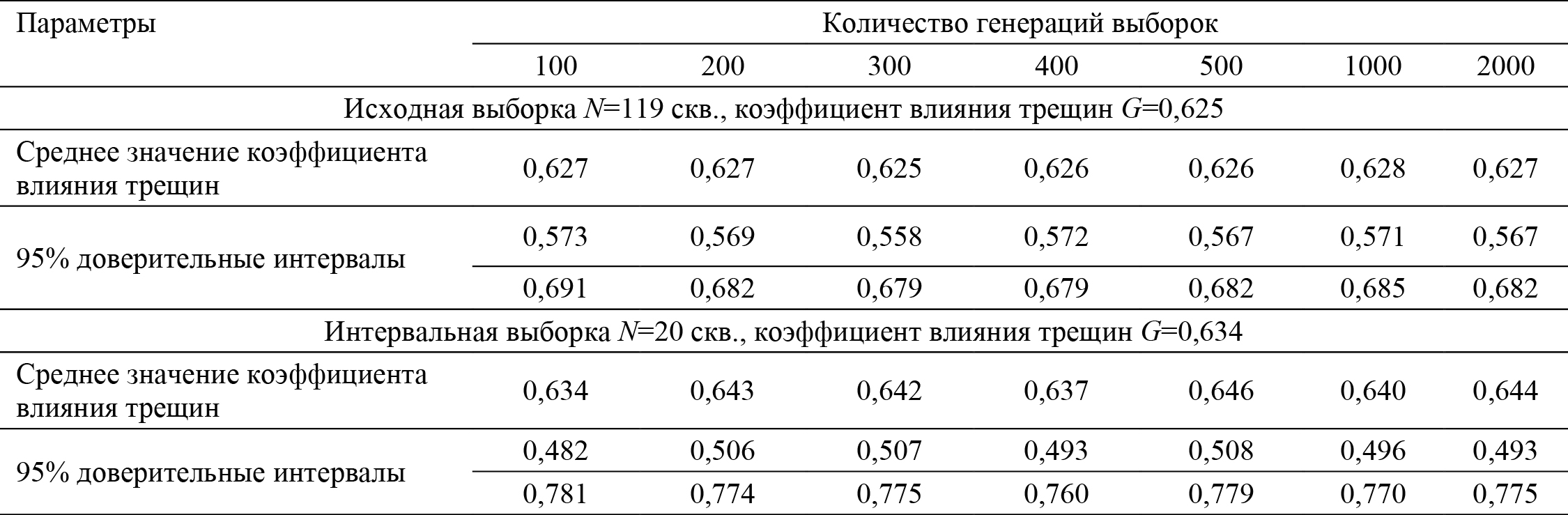
Табл. 1. Результаты бутстрепинга выборки скважин по накопленной добыче
Как показывает анализ результатов моделирования, исходное значение коэффициента влияния трещин попадет в доверительные интервалы, полученные по сгенерированным интервальным выборкам методом бутстрепинга. С увеличением количества генераций выборок значения доверительных интервалов существенно не меняются. Результаты моделирования свидетельствуют о возможности использования такого параметра как накопленная добыча для идентификации типа трещиноватого коллектора при небольшом количестве скважин. Следует отметить, что исследуемая совокупность скважин должна быть представительной и характеризовать исследуемый объект в полной мере.
Для оценки применимости при классификации трещиноватых коллекторов на ранних стадиях разработки такого показателя, как коэффициент продуктивности, выполним аналогичные исследования с уменьшением размеров выборок.
С применением бутстрепинга выполнена серия расчетов для начальных совокупностей данных по скважинам, соответствующих различным годам разработки:
- выборка из 110 скважин (30 год разработки), коэффициент влияния трещин по коэффициенту продуктивности GPI = 0,744;
- выборка из 53 скважин (10 год разработки), коэффициент влияния трещин по коэффициенту продуктивности GPI = 0,654;
- выборка из 12 скважин (3 год разработки), коэффициент влияния трещин по коэффициенту продуктивности GPI = 0,604.
Результаты моделирования представлены в табл. 2.
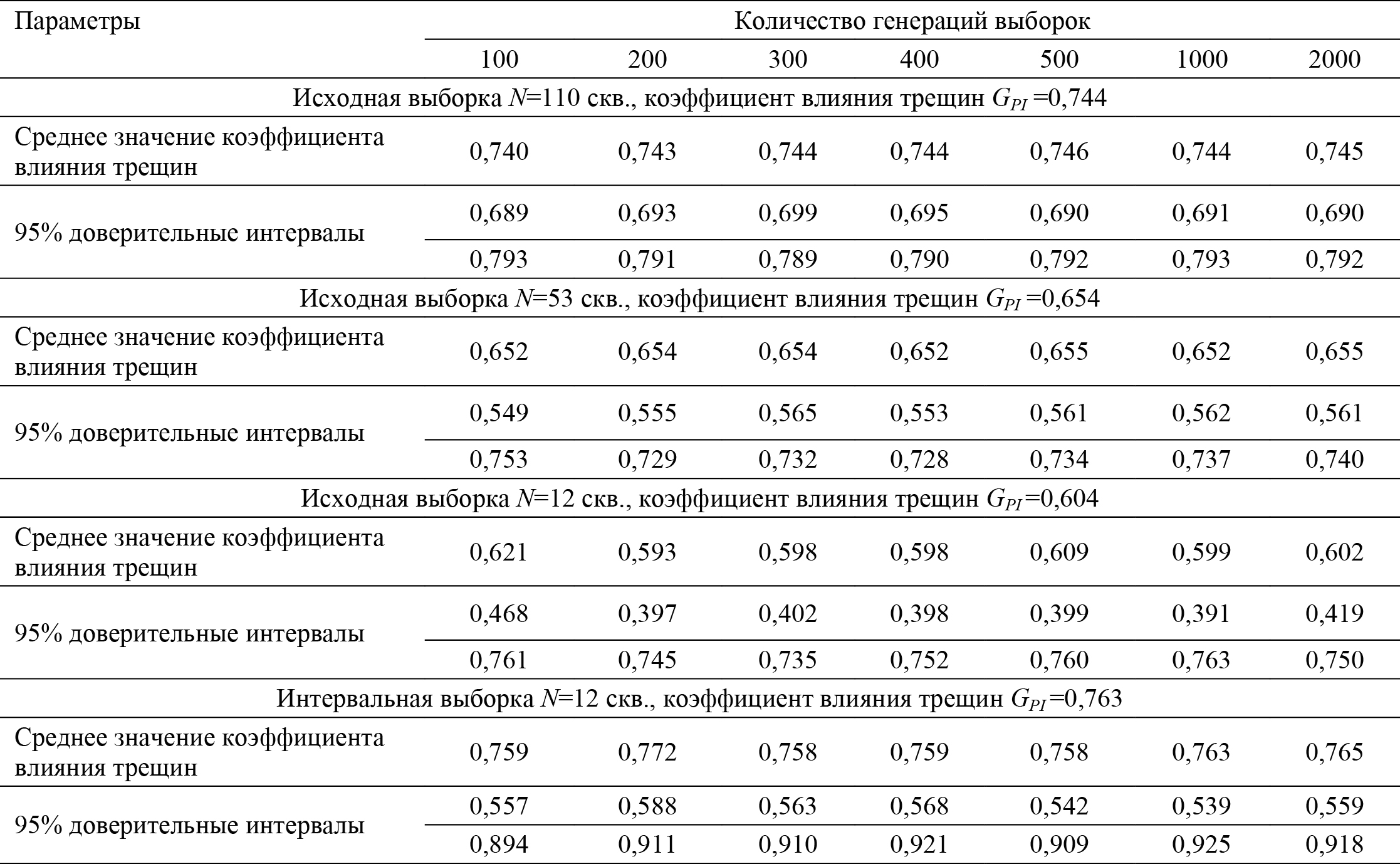
Табл. 2. Результаты бутстрепинга выборок скважин по коэффициенту продуктивности
Проанализировав результаты моделирования, можно отметить, что исходное значение коэффициента влияния трещин по коэффициенту продуктивности в большинстве случаев попадает в доверительные интервалы при исследовании выборки из 12 скважин в начальный период разработки.
Далее для подтверждения полученных выводов на основе выборки из 110 скважин после ранжирования их от меньшего к большему значению по коэффициенту продуктивности, выполнено создание интервальной выборки путем регулярного отбора каждой десятой скважины из исходного списка. Интервальная выборка включает 12 скважин, как и в выборке скважин на третий год разработки. Коэффициент влияния трещин интервальной совокупности скважин составил GPI = 0,763 (табл. 2). Как и в предыдущем случае при анализе накопленной добычи, использование такого подхода позволяет исследовать влияние увеличения границ формируемой совокупности данных. Сравнение результатов моделирования исходных выборок с интервальной показывает, что значение коэффициента влияния трещин (GPI = 0,744) попадает в доверительные интервалы по выборкам, сгенерированным методом бутстрепинга.
С одной стороны, результаты бутстрепинга исходных выборок данных по коэффициенту продуктивности на различные годы уверенно указывают на возможность использования такого параметра как коэффициент продуктивности для идентификации типа трещиноватого коллектора при небольшом количестве скважин. С другой стороны, результаты, полученные с использованием интервальной выборки, подтверждают, что для лучшего описания распределения трещиноватости по площади месторождения необходимо наличие представительной выборки данных.
Таким образом, для идентификации типа трещиноватого коллектора на ранних стадиях разработки с использованием коэффициента продуктивности необходимо обеспечить репрезентативную выборку скважин. Этого можно достичь путем размещения скважин по всей площади месторождения, даже при небольшом их количестве, что не противоречит принципам геологической разведки.
Заключение
Статья посвящена проблемам классификации трещиноватых коллекторов с использованием промысловых данных. Проведены исследования по оценке применимости показателя накопленной добычи и коэффициента продуктивности по скважинам для определения типа трещиноватого коллектора с использованием статистического метода анализа кривой Лоренца и коэффициента Джини (коэффициента влияния трещин) при небольших выборках данных и на начальных стадиях разработки.
Результаты предварительных исследований показали, что недостаточные и неравномерные накопленные объемы добычи нефти по скважинам показывают низкую достоверность для оценки коэффициента влияния трещин и построения кривой Лоренца на ранних стадиях разработки, поэтому когда накопленная добыча не может объективно отражать распределение трещинной неоднородности по коллекторам на ранних стадиях разработки, предлагается использовать коэффициент продуктивности скважин.
Для исследования коэффициента Джини (коэффициент влияния трещин) при небольшом фонде скважин использован один из методов математической статистики – бутстреп метод. Данный метод основан на многократной генерации множества случайных выборок из исходных данных и на их последующем статистическом анализе. Моделирование выборок проводилось при помощи генератора случайных чисел в электронных таблицах. Для исследования была использована исходная выборка скважин за более чем 20 летний период разработки месторождения в трещиноватых коллекторах.
По результатам исследований установлено, что применение для идентификации трещиноватых коллекторов при небольшом количестве скважин таких показателей, как накопленная добычи и коэффициент продуктивности, показало сопоставимые результаты. Для повышения достоверности классификации при небольшом количестве скважин требуется представительная выборка данных, которая будет наиболее полно описывать месторождение, что достигается путем размещения скважин на всей площади месторождения. На ранних стадиях разработки из-за незначительных объемов добываемой продукции и небольших сроков работы скважин для анализа рекомендовано использовать коэффициент продуктивности. Определение типа трещиноватого коллектора с начала разработки дает возможность предвидеть вероятное влияние трещин и запланировать пути решения потенциальных проблем, характерных для того или иного типа коллектора.
Благодарности
Автор выражает благодарность канд. техн. наук А.В. Хандзелю за многочисленные предложения и помощь в проведении моделирования.
Список литературы
1. Закревский К.Е., Кундин А.С. (2016). Особенности геологического 3D-моделирования карбонатных и трещинных резервуаров. М.: ООО «Белый Ветер», 404 с.
2. Мартюшев Д.А. (2014). Оценка трещиноватости карбонатных коллекторов вероятностно-статистическими методами. Нефтяное хозяйство, 4, с. 51–53.
3. Щекин А.И., Васильев В.А., Николайченко А.С., Коломийцев А.В. (2021). Промысловая классификация трещиноватых коллекторов кристаллического фундамента. Георесурсы, 23 (3), с. 90–98. doi: 10.18599/grs.2021.3.12
4. Aguilera R. (1995). Naturally fractured reservoirs. Tulsa, Oklahoma: PennWell Publishing Company, p. 521.
5. Ahr Wayne M. (2011). Geology of carbonate reservoirs: the identification, description, and characterization of hydrocarbon reservoirs in carbonate rocks. John Wiley & Sons, Inc, p. 296.
6. Akhkubekov A. E., Vasilyev V. N. (2010). Acid Tunneling Technology: Application Potential in Timan-Pechora Carbonates. SPE Russian Oil and Gas Conference and Exhibition. Moscow, Russia. doi: 10.2118/135989-MS
7. Allan Jack, Sun S. Qing. (2003). Controls on Recovery Factor in Fractured Reservoirs: Lessons Learned from 100 Fractured Fields. SPE Annual Technical Conference and Exhibition. Denver, Colorado. doi: 10.2118/84590-MS
8. Baker Richard O., Kuppe Frank (2000). Reservoir Characterization for Naturally Fractured Reservoirs. SPE Annual Technical Conference and Exhibition. Dallas, Texas. doi: 10.2118/63286-MS
9. Bourbiaux B. (2010). Fractured Reservoir Simulation: a Challenging and Rewarding Issue.Oil and Gas Science and Technology, 65(2), pp. 227–238. doi: 10.2516/ogst/2009063.
10. Dixon Philip M., Weiner Jacob, Mitchell-Olds Thomas, Woodley Robert. (1987). Bootstrapping the Gini Coefficient of Inequality. Ecology, 68(5), pp. 1548–1551. doi: 10.2307/1939238
11. Lorenz John C., Cooper Scott P. (2020). Applied Concepts in Fractured Reservoirs. John Wiley & Sons, Ltd, p. 240.
12. Manrique E., Thomas C., Ravikiran R., Izadi M., Lantz M., Romero J., Alvarado V. (2010). EOR: Current status and opportunities. SPE Symposium on Improved Oil Recovery. Tulsa, Oklahoma, USA, pp. 1584–1604. doi: 10.2118/130113-MS
13. Marchal D., Gonzalez I., Benito J., Balseiro P. (2005). Technologies and Exploitation Strategies Applied to the Development of a Naturally Fractured Carbonate Reservoir: The Cretaceous Cogollo Group in La Concepción Field, Maracaibo Basin, Venezuela. SPE Latin American and Caribbean Petroleum Engineering Conference. Rio de Janeiro, Brazil. doi: 10.2118/97384-MS
14. Mélard G. (2014). On the accuracy of statistical procedures in Microsoft Excel 2010. Computational Statistics, 29(5), pp. 1095–1128. doi: 10.1007/s00180-014-0482-5
15. Narr Wayne, Schechter David S., Thompson Laird B. (2006). Naturally Fractured Reservoir Characterization. Society of Petroleum Engineers, p. 112.
16. Nelson Ronald A. (1985). Geologic Analysis of Naturally Fractured Reservoirs. Gulf Publishing Company, Book Division, p. 320.
17. Nelson Ronald A. (2001). Geologic analysis of naturally fractured reservoirs. Gulf Professional Publishing, p. 352.
18. Nelson Ronald A. (2020). Static Conceptual Fracture Modeling: Preparing for Simulation and Development. John Wiley & Sons Ltd. doi: 10.1002/9781119596875.index
19. Spence Guy H., Couples Gary D., Bevan Tim G., Aguilera Roberto, Cosgrove John W., Daniel Jean-Marc, Redfern Jonathan (2014). Advances in the study of naturally fractured hydrocarbon reservoirs: A broad integrated interdisciplinary applied topic. Geological Society Special Publication, 374(1), pp. 1–22. doi: 10.1144/SP374.19
20. Sun S. Qing, Sloan Rod (2003). Quantification of Uncertainty in Recovery Efficiency Predictions: Lessons Learned from 250 Mature Carbonate Fields. SPE Annual Technical Conference and Exhibition. Denver, Colorado. doi: 10.2118/84459-MS
21. Sun Shaoqing, Pollitt David A. (2021). Optimising Development and Production of Naturally Fractured Reservoirs Using a Large Empirical Dataset. Petroleum Geoscience, 27(2). doi: 10.1144/petgeo2020-079
22. Tiab D., Donaldson E.C. (2015). Petrophysics. Gulf Professional Publishing. doi: 10.1016/C2014-0-03707-0
23. Toledo-Piña R., Leon-García A., Padilla-Sixto R. (2014). Water Injection in Offshore Naturally Fractured Reservoirs Associated to a Common Aquifer. SPE Latin America and Caribbean Petroleum Engineering Conference. Maracaibo, Venezuela. doi: 10.2118/169275-MS
24. Yitzhaki S., Schechtman E. (2013). The Gini methodology. A primer on a statistical methodology. New York: Springer, p. 548. doi: 10.1007/978-1-4614-4720-7
Об авторе
А. И. ЩекинРоссия
Александр Иванович Щекин, кандидат тех. наук, доцент
кафедра разработки и эксплуатации нефтяных и газовых месторождений
355035; пр. Кулакова, д. 16/1; Ставрополь
Рецензия
Для цитирования:
Щекин А.И. Применение статистических методов оценки трещиноватых коллекторов по промысловым данным. Георесурсы. 2025;27(1):275-283. https://doi.org/10.18599/grs.2025.1.3
For citation:
Shchekin A.I. Applying Statistical Methods to Assess Fractured Reservoirs Relying on Field Data. Georesursy = Georesources. 2025;27(1):275-283. (In Russ.) https://doi.org/10.18599/grs.2025.1.3
















.png)


