Перейти к:
Решение обратной задачи определения начального компонентного состава углеводородов газоконденсатного месторождения по известным промысловым данным
https://doi.org/10.18599/grs.2024.3.9
Аннотация
Работа посвящена вопросу определения композиционного состава пластового газа для газоконденсатных месторождений. Предложена методика планирования газоконденсатных исследований (ГКИ), которая позволяет оценить возможность получения кондиционных проб пластового флюида. Для случая, когда отбор кондиционных проб невозможен, разработан подход для их интерпретации. На первом шаге предлагается численно создавать набор композиционных составов добавлением к лабораторному составу «обедненного» газа некоторого количества равновесного ему конденсата. Получаемые композиционные составы имеют различные давления начала конденсации выше давления начала конденсации лабораторного газа. На втором шаге для каждого из полученных составов проводится гидродинамическое (ГД) моделирование и выбирается состав, для которого расчетные значения дебитов конденсата, газа и газоконденсатного фактора (ГКФ) близки к данным ГКИ. Анализ численных экспериментов на синтетических данных для характерной скважины показал существенную зависимость ГКФ от компонентного состава и малую чувствительность к изменениям основных параметров ГД-модели. При настройке ГД-модели на фактические замеры предложено сначала из набора восстановленных составов выбрать состав, для которого модельные значения ГКФ будут наиболее близкими к фактическим, затем при фиксированном выбранном составе производить подбор остальных параметров ГД-модели по данным дебитов газа и конденсата. Предложенная методика апробирована для одной реальной скважины для определения компонентного состава и основных параметров пласта по данным ГКИ.
Ключевые слова
Для цитирования:
Гимазов А.А., Имомназаров Б.Х., Старовойтова Б.Н., Байкин А.Н., Бабин В.М., Хамидуллин Д.Ф., Купоросов Д.Н. Решение обратной задачи определения начального компонентного состава углеводородов газоконденсатного месторождения по известным промысловым данным. Георесурсы. 2024;26(3):73-86. https://doi.org/10.18599/grs.2024.3.9
For citation:
Gimazov A.М., Imomnazarov B.Kh., Starovoytova B.N., Baykin A.N., Babin V.M., Khamidullin D.F., Kuporosov D.N. Solution of the Inverse Problem of Determining the Initial Hydrocarbons Composition in a Gas-Condensate Reservoir Using Field Data. Georesursy = Georesources. 2024;26(3):73-86. (In Russ.) https://doi.org/10.18599/grs.2024.3.9
Введение
Получение корректных данных по составу и свойствам пластового газа на газоконденсатных объектах имеет принципиально важное значение. Широкий диапазон неопределенности в этих данных существенно повышает риски неверных инвестиционных решений, ошибочных прогнозных профилей добычи газа и в особенности конденсата. Однако в условиях низкой проницаемости и высокого потенциального содержания тяжелых компонент в пластовом газе отбор кондиционных проб затруднен и часто невозможен по объективным причинам. Отбор лабораторных проб при высоких депрессиях приводит к выпадению (потери) тяжелых компонент (С5+-фракций), которые играют важную роль в определении термофизических (PVT) свойств газоконденсатной смеси (ГКС). Например, давление начала конденсации (Pнк) пластового флюида зависит от мольного содержания и молекулярного веса тяжелых фракций (Elsharkawy, 2002).
В таких случаях можно использовать подход, когда проводится отбор обедненных проб пластового флюида с последующим их «донасыщением» до состояния пластового газа. Подход к решению задачи донасыщения должен быть комплексным и включающим в себя планирование исследований в поле и лабораторных условиях, а также последующую их интерпретацию. Для этого требуется дополнительная информация, которая в стандартных исследованиях не всегда фиксируется, поэтому необходимо проводить планирование исследования, которое будет учитывать типы компоновки и заканчивания скважины, даст оценку возможности отбора кондиционных проб и способно спрогнозировать осложнения, которые могут возникнуть в ходе проведения исследования.
В работе (Osfouri, Azin, 2016) рассмотрены основные проблемы, возникающие при заборе и последующей рекомбинации лабораторных проб. Подчеркнута важность требования, чтобы газ сепарации и конденсат находились в состоянии термодинамического равновесия в момент отбора. В (Reffstrup, Olsen, 1994) предложена следующая методика восстановления пластового флюида: газ сепарации и равновесный ему конденсат пошагово рекомбинируются до давления начала конденсации, равного пластовому давлению. В (Fevang, Whitson, 1994) представлены экспериментальные подходы к восстановлению составов исходной газоконденсатной смеси по известным составам газа сепарации и стабильного конденсата для случая, когда давление пласта ниже давления начала конденсации и в пласте имеется выпавший конденсат. Однако эти подходы не апробировались на реальных данных. В работе (Bonyadi et al., 2014) описана численная и экспериментальная методика одновременного донасыщения отобранных на сепараторе проб газа равновесным ему конденсатом и определения газоконденсатного фактора (ГКФ). В работах (Брусиловский, Промзелев, 2013; Брусиловский, Ющенко, 2016; Schebetov et al., 2010; Promzelev et al., 2018) представлены численные методики восстановления композиционных составов, позволяющие поднять давление начала конденсации до пластового давления с использованием только PVT-данных флюида. Следует подчеркнуть, что во всех методиках донасыщения истинным давлением начала конденсации считается пластовое давление, а влияние процессов фильтрации в пласте и данные газоконденсатных исследований (ГКИ) не учитываются. Однако, как показывает практика, газоконденсатные месторождения могут характеризоваться недонасыщенностью (Лапшин и др., 2019), и для таких месторождений Pнк пластового флюида не равно пластовому давлению.
Целью настоящей работы является разработка способа подбора начального компонентного состава пластового газа по данным исследования проб, «обедненных» вследствие выпадения конденсата при высоких депрессиях отбора, методом сравнения результатов гидродинамического (ГД) моделирования ГКИ с фактическими данными дебитов газа и конденсата. Аналогичный подход применялся в (Yang et al., 2020), где использовался генетический многокритериальный оптимизационный алгоритм для определения композиционного состава в пласте на примере одного из месторождений Китая. Однако в указанной работе предполагалось, что существуют репрезентативные пробы, отобранные в соответствии с рекомендациями (Osfouri, Azin, 2016) в начальный период разработки пласта. Подбор исходного композиционного состава осуществлялся с помощью ГД-моделирования с момента запуска скважины в работу до момента забора пробы по минимизации разницы между модельным и промысловым дебитом газа и минимизации суммарной покомпонентной невязки между искомым составом и составом пробы.
В настоящей работе сначала проведено сравнение двух численных подходов к донасыщению тяжелыми компонентами композиционного состава реального пластового флюида при наличии некондиционной пробы. Далее разработанный способ подбора подходящего состава ГКС на основе решения обратной задачи гидродинамического моделирования проверен на корректность на синтетических данных. Предложенная методика апробирована на данных с реальной скважины.
Материалы и методы
В работе предполагается, что пробы пластового газа отобраны при больших депрессиях и поэтому являются обедненными. Для этих проб проведены лабораторные исследования, создана и настроена PVT-модель флюида. Под настройкой PVT-модели понимается калибровка свойств тяжелых компонент и коэффициентов бинарного взаимодействия таким образом, чтобы результаты численного моделирования с помощью уравнения состояния экспериментов типа дифференциального разгазирования (CVD) и контактного разгазирования (CCE) совпадали с данными лабораторных исследований.
Предлагается определять исходный компонентный состав пластового газа, объединив методику численного донасыщения отобранных проб тяжелыми компонентами и ГД-моделирование ГКИ:
1) на первом шаге для обедненного начального композиционного состава проводится его численное донасыщение тяжелыми компонентами в несколько шагов и создаются N различных составов с разными давлениями начала конденсации от начального до пластового.
2) на втором шаге для каждого из полученных N составов-кандидатов проводится ГД-моделирование, и композиционный состав, при использовании которого ГД-модель дает показатели дебитов, наиболее близкие к данным геологического журнала (ГЖ), считается искомым.
Таким образом, задача определения исходного композиционного состава пластового газа относится к классу обратных задач, когда входные параметры модели определяются по данным наблюдения.
В работе используется PVT-модель реальной скважины с месторождения X, компонентный состав которой и основные свойства компонент представлены в табл. 1.
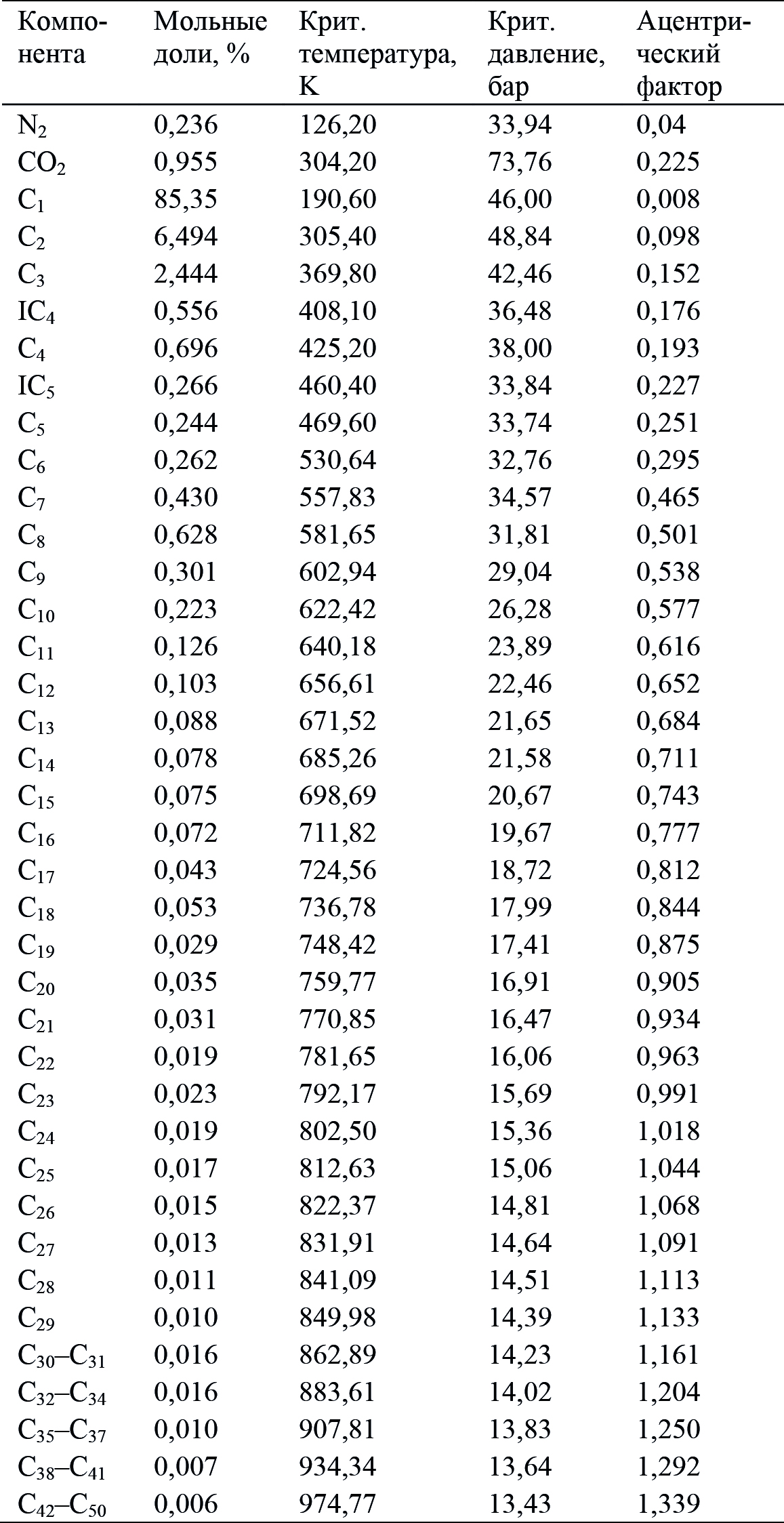
Табл. 1. Компонентный состав и основные свойства
компонент газоконденсатной смеси с реальной скважины месторождения X
Гидродинамическая модель пласта считается упрощенной в том смысле, что пласт представляется однородным, однослойным и изолированным, вода присутствует только в виде остаточной насыщенности, а пластовый флюид представлен фазами конденсата и газа. При этом параметры пласта и относительных фазовых проницаемостей (ОФП) выбираются средними, характерными для данного месторождения.
Для решения обратной задачи о нахождении компонентного состава необходимо сформулировать прямую задачу о фильтрации ГКС в пласте и притоке к горизонтальной скважине.
1.1 Постановка прямой задачи о течении многокомпонентного флюида в пласте
Рассмотрим задачу о притоке газоконденсатной смеси к одиночной горизонтальной скважине, на которой проведен множественный гидроразрыв пласта (МГРП). Предположим, что имеется однородный и однослойный продуктивный пласт мощности H, который представляется в виде пористой среды c пористостью ϕ и проницаемостью k. В порах горной породы находится углеводородная смесь из Nc компонент, которые могут находиться в газообразной (газ) или жидкой (конденсат) фазах. Фильтрация данного флюида в пласте моделируется на основе двухфазной композиционной модели (газ и конденсат). Для каждой из компонент выполняется закон сохранения массы, а движение фаз подчиняется закону Дарси. Вода присутствует как неподвижная пассивная фаза с заданной начальной насыщенностью. Кроме того, предполагается, что в любой момент времени система газ – конденсат находится в термодинамическом равновесии. Для замыкания системы уравнений необходимо задать уравнение состояния пластового флюида, например Пенга – Робинсона, и зависимости капиллярного давления и ОФП от насыщенности газом. Рассматриваемый сектор месторождения считается изолированным, поэтому на всех внешних границах задается условие непротекания. Данная система уравнений является общепринятой и описана подробно во многих источниках, например в (Myron, 2021).
Закрепленные трещины гидроразрыва пласта (ГРП) ориентированы перпендикулярно скважине и характеризуются полудлиной xf, эффективной шириной wf и проницаемостью проппантной пачки kf. Течение в каждой трещине подчиняется соответствующим усредненным по трещине законам сохранения массы и закону Дарси.
На скважине давление в фазах полагается равным забойному давлению Pзаб, заданному одинаковым вдоль всей горизонтальной части ствола без учета трения.
В начальный момент времени давление в пласте полагается равным Pпл и считается, что изначально в пласте находился только газ с остаточной водной фазой фиксированной насыщенности.
В настоящей работе расчет прямой задачи проводится с использованием академической лицензии симулятора tNavigator (tNavigator 23.1, 2023).
Результаты и обсуждение
2.1 Методика планирования ГКИ
При планировании ГКИ необходимо учитывать промысловые и технологические ограничения. Так, согласно Инструкции Газпрома (Р-Газпром, 2011), при проведении ГКИ создаваемая на пласт депрессия должна быть не более 10% для полностью насыщенных залежей. Существует также ограничение на минимально необходимую скорость восходящего потока на башмаке насосно-компрессорной трубы (НКТ), определенную по критериям сохранения дисперсно-кольцевого потока в вертикальных трубах – не менее 2,5 м/с, согласно Инструкции Газпрома. Минимальную скорость также можно рассчитать по другим методикам (Turner et al., 1969; Коротаев, Ширковский, 1984).
Однако для низкопроницаемых коллекторов не всегда возможно удовлетворить одновременно критерию минимальной скорости выноса с башмака НКТ (требуется высокая депрессия и дебит) и ограничению максимальной депрессии на пласт (требуется не превысить рекомендованную депрессию). На рис. 1. приведен пример характеристик двух скважин: высоко- и низкопродуктивной. Для высокопродуктивной скважины режимы с достаточной скоростью на башмаке НКТ (Коротаев, Ширковский, 1984) достигаются при дебитах, находящихся правее точки А (рис. 1). Режимы с депрессией менее 10% (от величины пластового давления) – левее точки В. Таким образом, для высокопродуктивной скважины существует некоторый диапазон для проведения ГКИ. Однако для низкопродуктивной скважины минимальная скорость выноса достигается лишь при депрессии более 60%, что приводит к отбору некондиционной пробы.
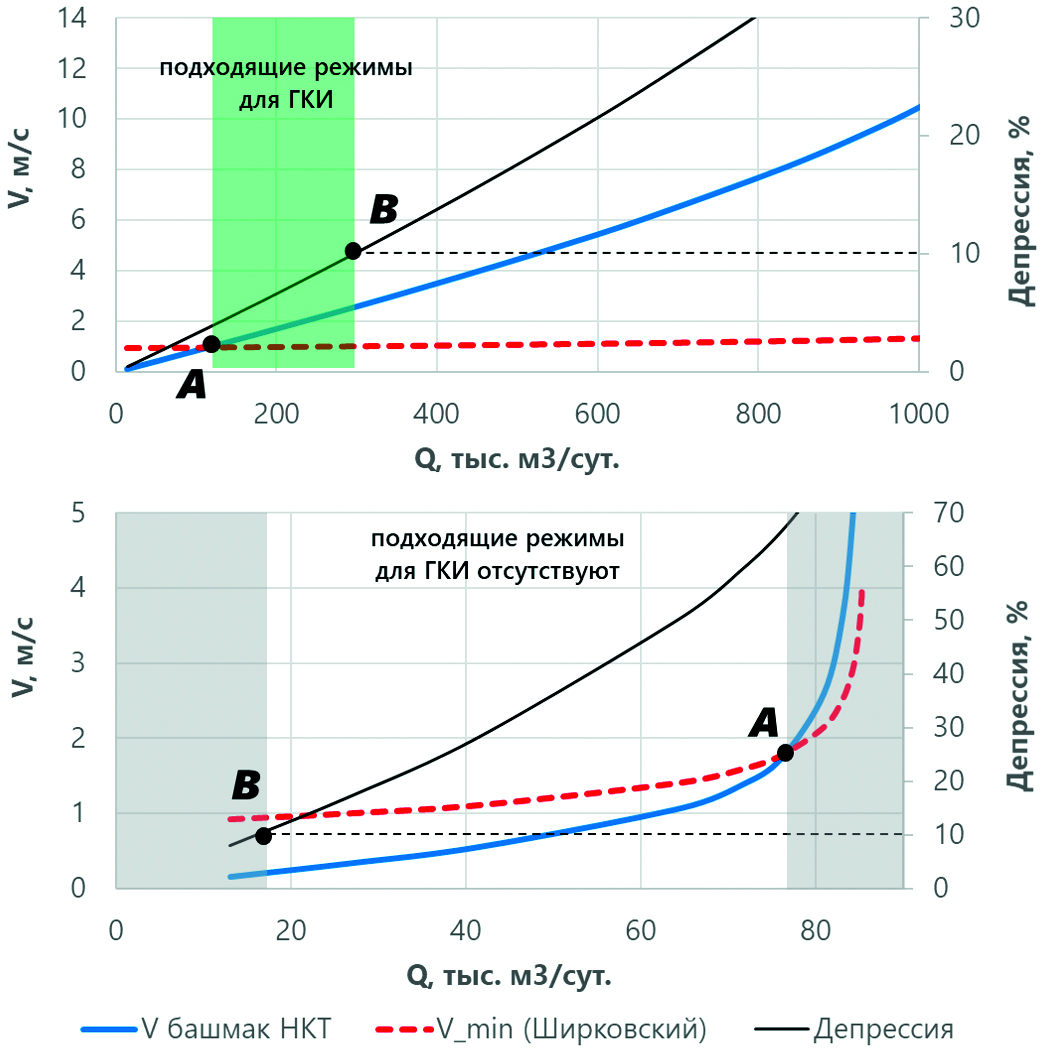
Рис. 1. Пример подбора режимов ГКИ
для высокопродуктивной скважины (сверху)
и низкопродуктивной скважины (снизу).
Зеленым отмечен допустимый диапазон для проведения ГКИ
Таким образом, возникает задача определения истинного композиционного состава пластового флюида по его некондиционным пробам.
При отборе проб существуют также другие ограничения, связанные с работой оборудования на поверхности: унос капель жидкости в газе, гидратообразование в поверхностной обвязке, выпадение парафинов в сепарационной емкости, а также ограничения по скорости течения в трубах. Влияние данных ограничений на планирование ГКИ и выбор режимов будут рассмотрены в отдельной работе.
2.2 Методика восстановления состава пластовой газоконденсатной смеси
Во всех численных и экспериментальных методиках восстановления пластового флюида (Брусиловский, Промзелев, 2013; Брусиловский, Ющенко, 2016; Schebetov et al., 2010) предлагается смешивать состав лабораторного газа с равновесным ему конденсатом, повышая тем самым давление начала конденсации получающейся смеси. Пусть имеется начальный газ (Газ0) с компонентным составом C0, пластовой температурой Т0 и давлением начала конденсации Pнк0 ниже заданного пластового давления Pпл. Требуется получить набор композиционных составов {Газ1, Газ2, Газ3,…, ГазN} с давлениями начала конденсации равными Pнк0 < Pнк1 < Pнк2 <… < PнкN = Pпл соответственно. Указанное множество давлений начала конденсации считается заданным. Рассматривается изотермический случай, когда температура всех составов равна температуре начального состава T0.
В работах (Брусиловский, Промзелев, 2013; Promzelev et al., 2018) предлагается последовательно добавлять на i-м шаге к пластовому газу Газi с Pнкi такое количество равновесного ему конденсата, чтобы получался новый состав газа Газi+1 с требуемым давлением начала конденсации Pнкi+1. Такой подход назовем подходом 1 со схемой довосстановления, приведенной на рис. 2. Таким образом, композиционный состав с давлением начала конденсации, равным пластовому давлению, получается последовательным восстановлением составов.
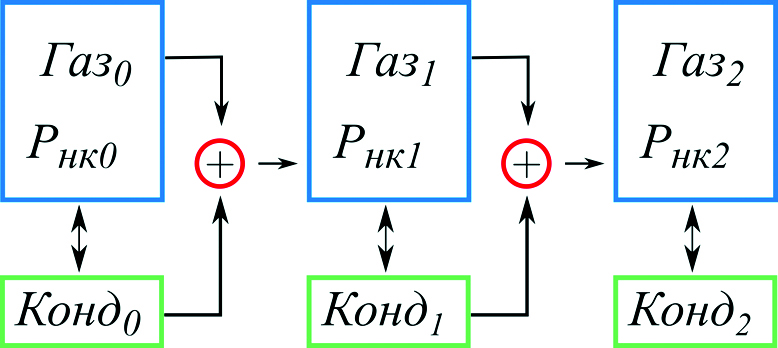
Рис. 2. Схема довосстановления составов для подхода 1.
Кондi обозначает равновесный к Газi конденсат.
Однонаправленные стрелки обозначают смешивание (+) и получение нового состава.
Двунаправленные стрелки обозначают равновесность
В настоящей работе предлагается альтернативный метод, аналогичный (Schebetov et al., 2010), когда довосстановление производится до требуемого давления Pнкi за один шаг. Считается, что начальный состав С0 может быть получен обеднением некоторых различных составов C1, C2, …, CN с разными давлениями начала конденсации, равными соответственно Pнк1, Pнк2,…, PнкN. Иными словами, при приведении этих различных составов к давлению p = Pнк0 они все дают исходный состав С0. Таким образом, составы с разными Pнк получаются в результате смешивания Газ0 и Конд0 в разных пропорциях. Схема довосстановления составов при таком подходе, который назовем подход 2, приведена на рис. 3.
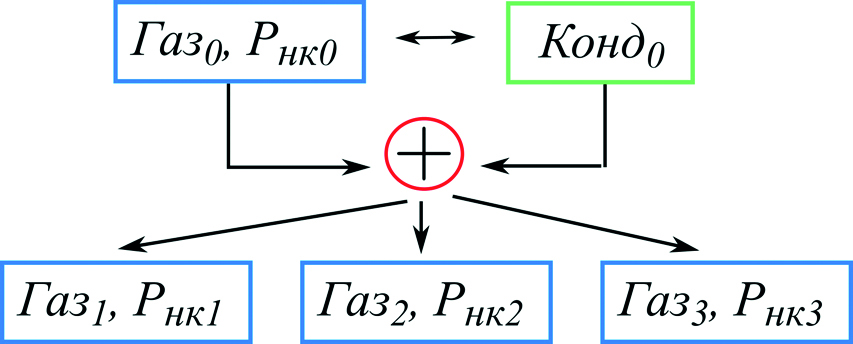
Рис. 3. Схема довосстановления составов для подхода 2.
Обозначения см. на рис. 2
Критерием состоятельности процедуры довосстановления композиционного состава является требование того, чтобы восстановленный состав при его приведении к начальному давлению p = Pнк0 соответствовал поведению начального состава С0. При разработке газоконденсатных месторождений важной характеристикой являются оценка потенциального содержания тяжелых компонент на пластовый газ (ПС5+) и кривая потерь конденсата, поэтому при анализе методик довосстановления состава будем опираться на эти кривые.
Предлагается сравнить две методики довосстановления на PVT-модели реального пластового флюида (табл. 1) с пластовой температурой 109 °С и Pнк = 537 бар. Исходный компонентный состав (табл. 1) в PVT-дизайнере (tNavigator 23.1, 2023) приводится к термодинамическому равновесию при давлении в 250 бар. Получаемый при этом состав газа принимается за обедненный начальный состав C0 с Pнк0 = 250 бар. Затем проводятся процедуры довосстановления состава C0 до исходного с Pнк = 537 бар двумя подходами, так чтобы давления начала конденсации Pнкi были равны 284, 349, 405, 442, 470, 493, 512, 527, 537 бар. Восстановленные составы, полученные с помощью подхода 1 и подхода 2, назовем как состав 1 и состав 2 соответственно и проведем их сравнение с исходным.
Кривые потери конденсата и ПС5+ рассчитываются по результатам моделирования процесса разгазирования (CVD) в PVT-дизайнере (tNavigator 23.1, 2023) с шагом по давлению в 20 бар, т.е. всего 27 ступеней с давлениями 537, 517, 497, …, 17 бар. На каждой ступени по определяемому компонентному составу газа рассчитывается ПС5+ в соответствии с (ГОСТ Р 57851.4–2017, 2017).
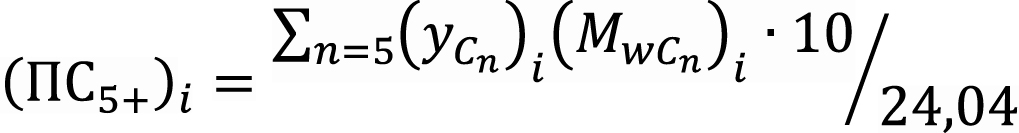 , (1)
, (1)
где i – номер ступени разгазирования, i = 0 соответствует давлению 537 бар, n – карбоновое число, (yCn)i и (MwCn)i – молярная доля (%) компоненты с карбоновым числом n и ее молекулярная масса (г/моль) на i-й ступени соответственно, 24,04 – молярный объем в стандартных условиях (дм3/моль). Потери конденсата рассчитываются как разница между ПС5+ состава при стартовом давлении в 537 бар и ПС5+ состава газа на каждой ступени.
На рис. 4 приведены кривые ПС5+ и потерь конденсата в зависимости от давления для исходного состава и для восстановленных составов по двум подходам. Графики на рис. 4 демонстрируют, что кривые ПС5+ и потерь конденсата (кривые 1 и 3 соответственно) для исходного и восстановленного по подходу 2 составов совпадают. Довосстановление по подходу 1 дает более «бедный» по ПС5+ состав (кривая 2), чем по подходу 2, и занижает потери конденсата (кривая 4) по сравнению с исходным составом.
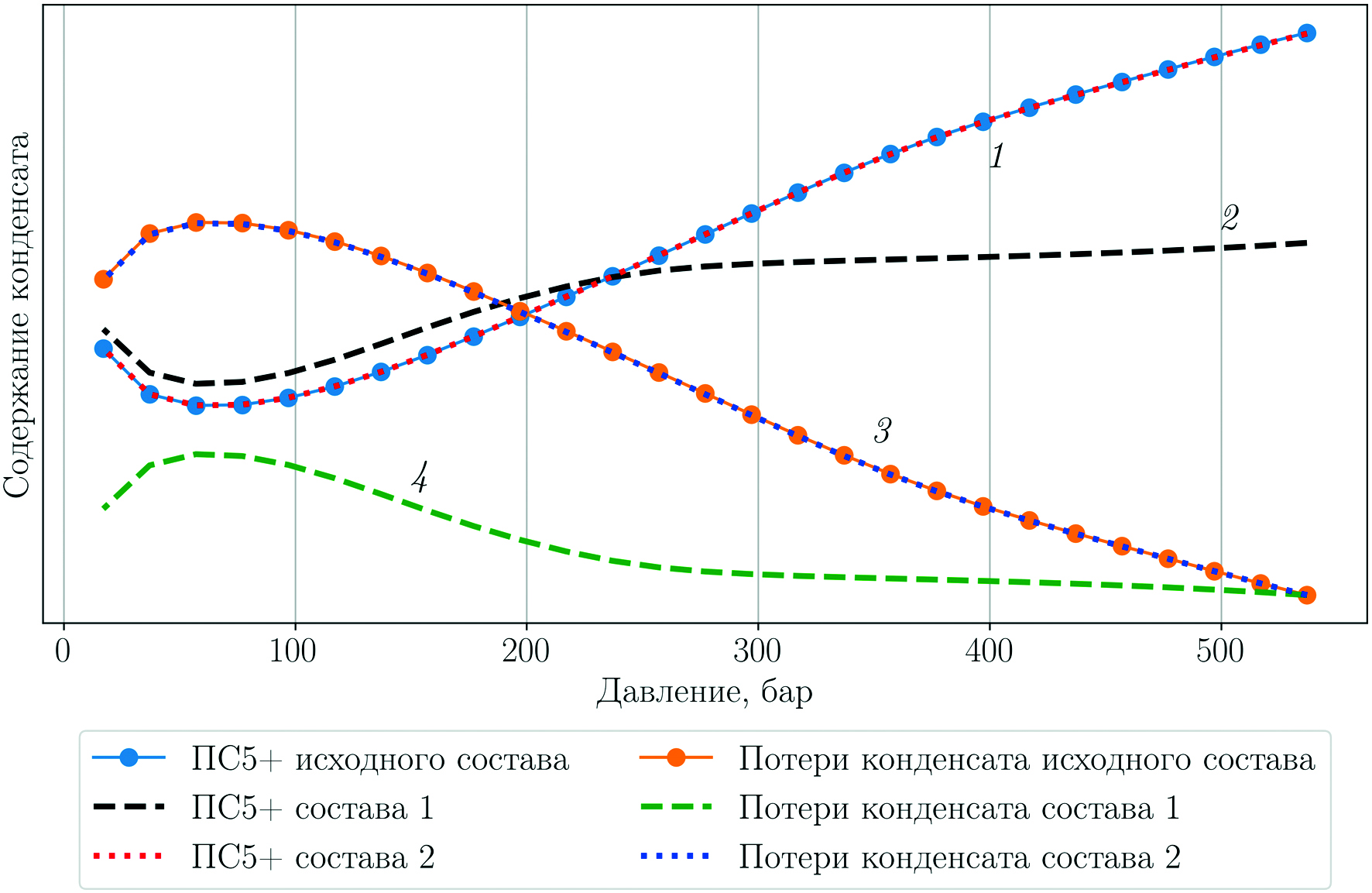
Рис. 4. Кривые ПС5+ и потерь конденсата для исходного состава
и восстановленных по подходу 1 (состав 1) и по подходу 2 (состав 2).
Цифрами обозначены линии для удобства описания в тексте
Покомпонентные ошибки в процентах для восстановленных по двум подходам составов по отношению к исходному составу представлены на рис. 5, где величина ошибки по оси Oy откладывается в логарифмическом масштабе. Углеводородные компоненты упорядочены по возрастанию карбонового числа.
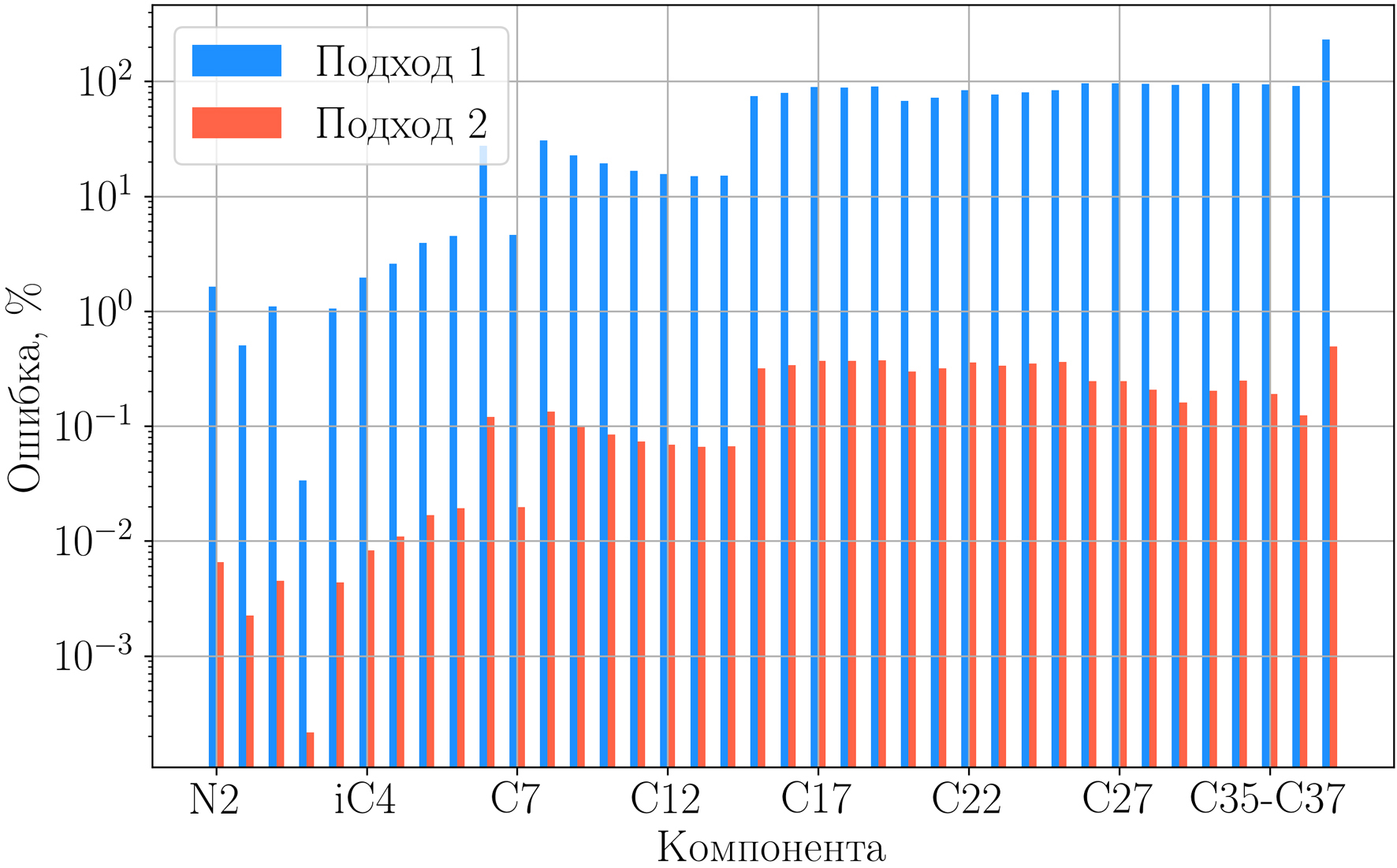
Рис. 5. Относительная ошибка мольного содержания компонент
по отношению к исходному составу для восстановленных по двум подходам составов
Отметим, что ошибки по легким компонентам до nC5 включительно для обоих подходов малы. Однако с ростом карбонового числа покомпонентная ошибка по подходу 1 растет и в последней псевдокомпоненте С45–С50 достигает 200%. В свою очередь, подход 2 дает состав практически идентичный исходному, поскольку разброс ошибки по мольным долям не превышает 0,5%. Таким образом, подход 1 хотя и дает состав с Pнк равным исходному, но не воспроизводит показатели ПС5+ и дает большую погрешность в мольных долях компонент. В дальнейшем будет использоваться только подход 2.
2.3 Решение обратной задачи об определении начального компонентного состава на синтетических данных
Проведем апробацию предлагаемого в работе подхода к определению композиционного состава на синтетических данных. Для такой постановки задачи фактические исторические данные дебитов газа и конденсата генерируются расчетом на ГД-модели при подстановке некоторого компонентного состава в качестве фактического. Пластовое давление принимается равным 600 бар и используется PVT-модель из табл. 1.
Вначале генерируются 3 обедненных состава приведением исходного (табл. 1) к давлению 250, 300, 350 бар соответственно. Затем проводится довосстановление этих обедненных составов подходом 2, и создается 25 композиционных составов с разными давлениями Pнк от давлений (250, 300, 350 бар) до пластового. В качестве фактического выбирается состав с Pнк = 506,08 бар (табл. 2), восстановленный от обедненного состава с Pнк = 250 бар и исключенный в дальнейшем из перебора.
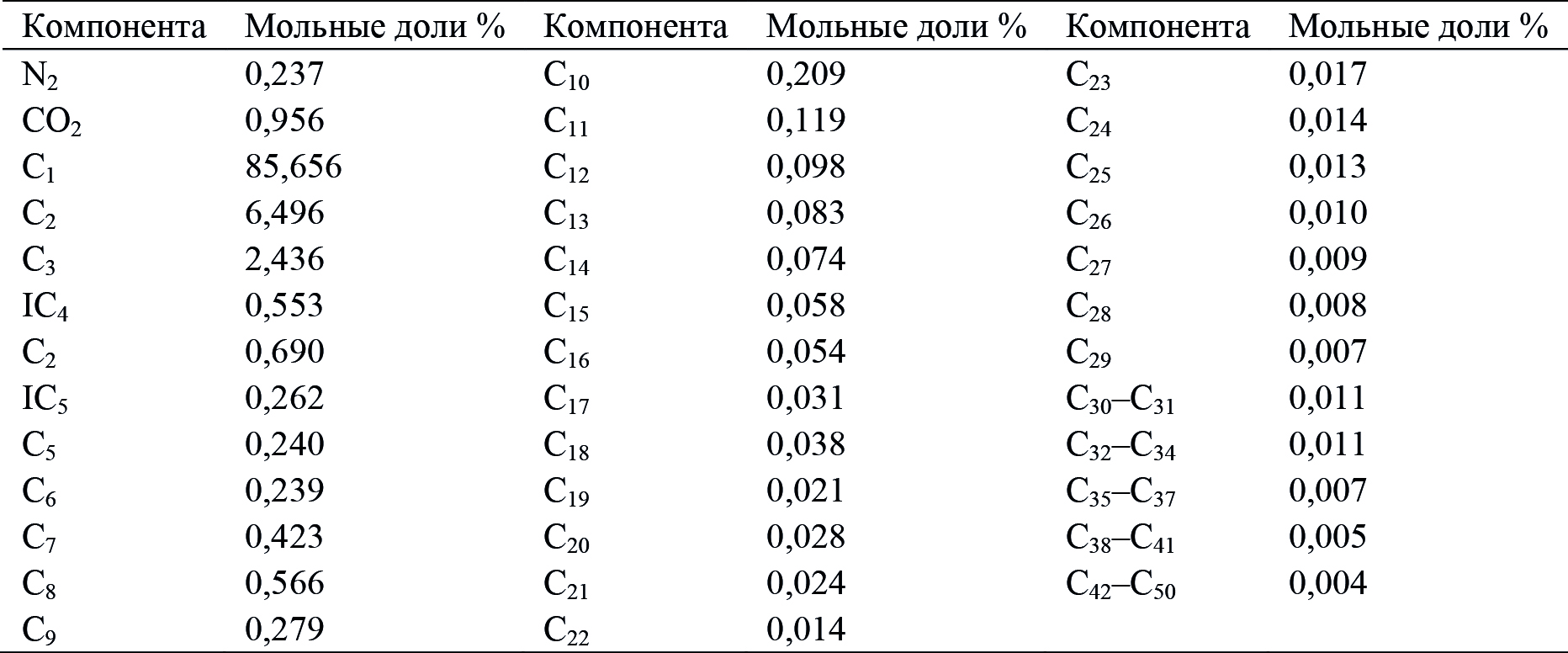
Табл. 2. Фактический композиционный состав,
используемый при решении обратной задачи на синтетических данных
2.3.1 Гидродинамическая модель в симуляторе tNavigator
Для решения прямой задачи как элемента решения обратной создается ГД-модель в симуляторе tNavigator. В рамках рассматриваемой постановки задачи о моделировании газоконденсатных исследований будем предполагать, что продуктивный пласт является однородным и представляет собой параллелепипед размером 4000 × 4000 × 25 м по осям X, Y, Z соответственно. Ось Z направлена вниз. Горизонтальная скважина находится в центре пласта. На скважине проведен МГРП с 6 трещинами ГРП, расположенными равноудаленно друг от друга и ориентированными перпендикулярно стволу. Основные параметры пласта и трещин приведены в табл. 3.
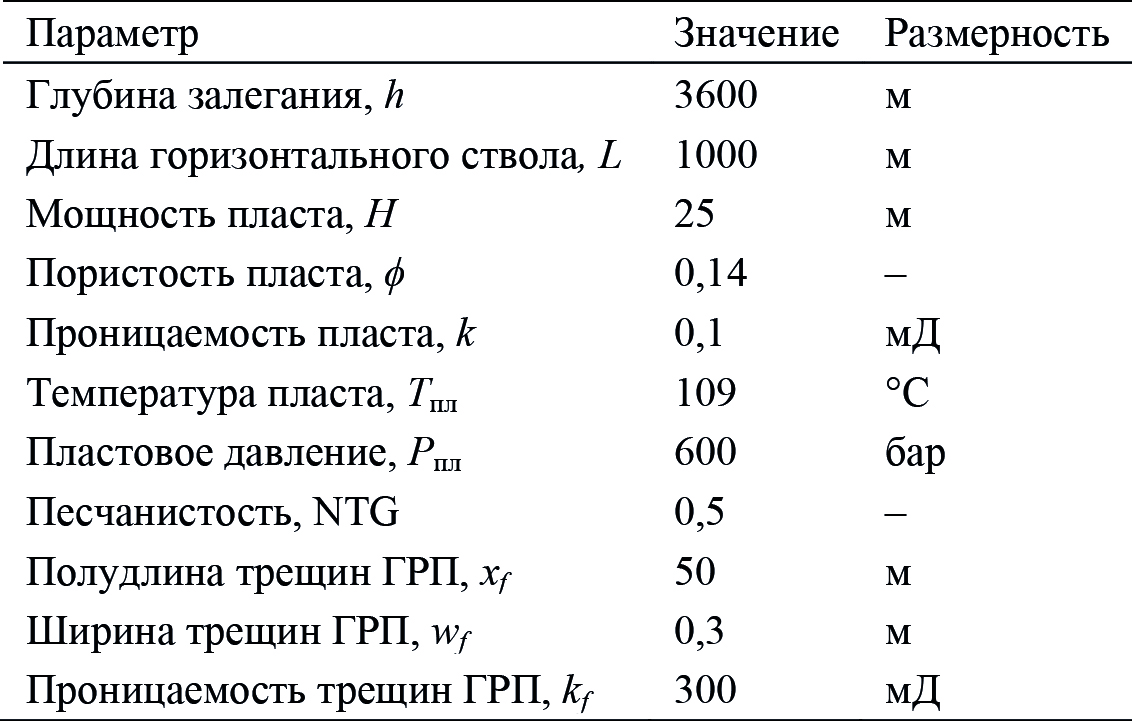
Табл. 3. Параметры пласта и трещин, используемые в ГД-модели по умолчанию
Дискретизация области и уравнений модели производится согласно функциональности симулятора tNavigator. Вдоль ствола скважины и в окрестности трещин размер ребра расчетных блоков составляет 10 м. В остальных частях расчетной области размер блока увеличивается по мере удаления от ствола скважины до 200 м на границе области. Схема пласта вблизи скважины и поле давления в плоскости XY в некоторый момент времени t приведены на рис. 6.
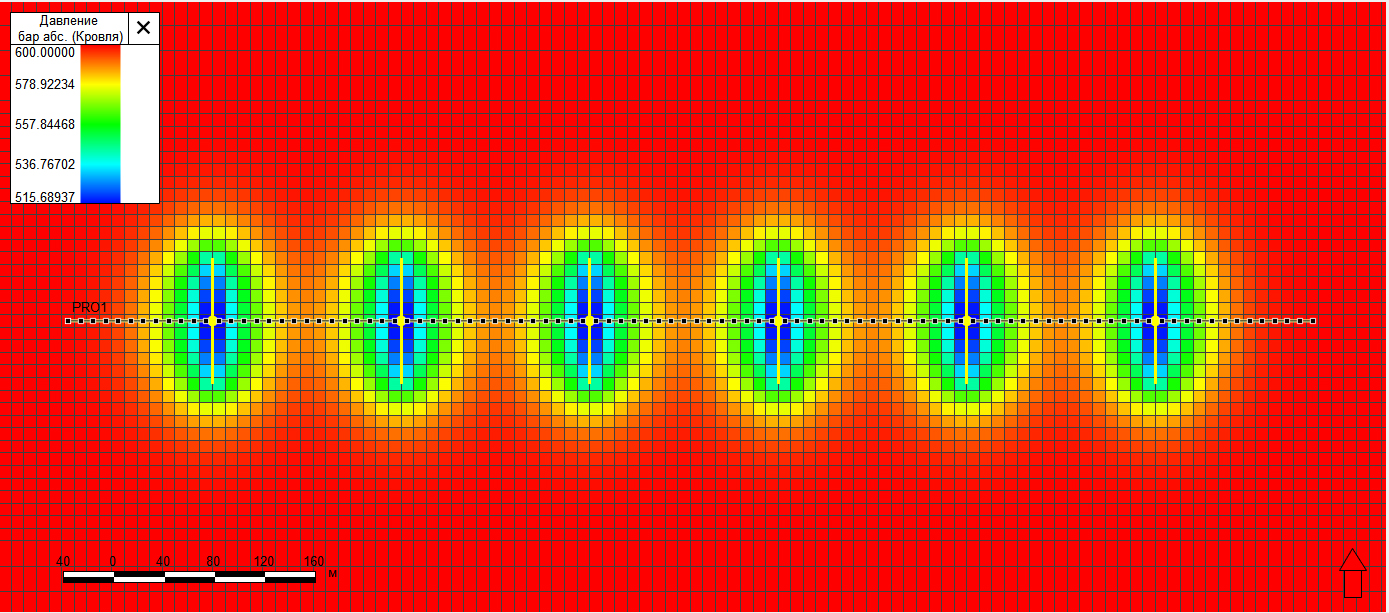
Рис. 6. Схема пласта в окрестности скважины c МГРП в сечении плоскостью XY.
Картой показан расчет давления в tNavigator в некоторый момент времени
Относительные фазовые проницаемости моделируются корреляциями Кори для систем газ – конденсат и вода – конденсат со значениями концевых точек ОФП, представленными в табл. 4. Здесь для системы газ – конденсат введены следующие обозначения: SGL, SGU, SGCR – минимальная, максимальная и критическая насыщенности газом соответственно, SOGCR – критическая насыщенность конденсатом, krGR, krORG, nG, nOG – проницаемость по газу при остаточной насыщенности конденсатом, проницаемость по конденсату при остаточной насыщенности газом, степени Кори по газу и конденсату соответственно, pcOG, npG – значение капиллярного давления и степень для капиллярного давления соответственно. Для системы вода – конденсат параметры SWL, SWU, SWCR, SOWCR, krWR, krORW, nW, nOW, pcOW, npW имеют аналогичный смысл.
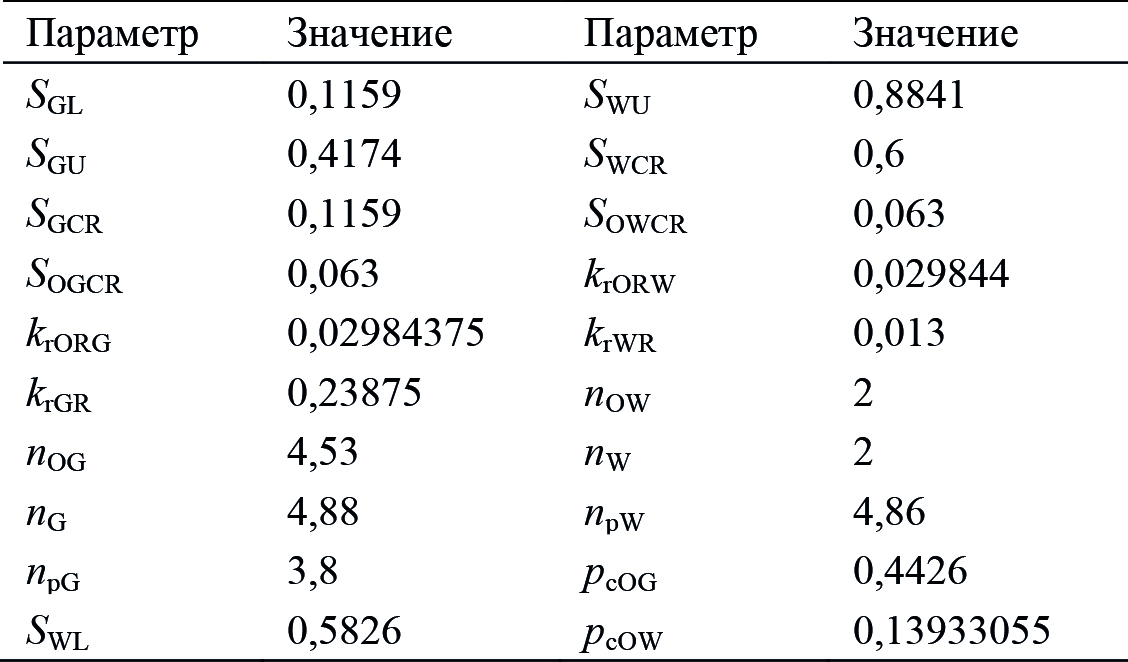
Табл. 4. Значения концевых точек ОФП
Исследование скважины моделируется четырьмя режимами работы скважины с различными значениями депрессий, равными 72, 108, 153 и 109,5 бар, и продолжительностью 2, 2, 3 и 5 дней соответственно.
2.3.4 Решение обратной задачи по подбору состава в отсутствии неопределенности в остальных параметрах модели
Для решения обратной задачи использован модуль адаптации симулятора tNavigator (tNavigator 23.1, 2023). При этом в качестве составов-кандидатов взяты восстановленные составы, приведенные в табл. 5 с указанием номера состава, давления начала конденсации начального состава (от которого проводилось восстановление), давления начала конденсации восстановленного состава и его ошибка по ПС5+ в процентах по отношению к фактическому составу. В качестве метода адаптации выбирается перебор по сетке составов, а для целевых функций используются невязки по дебитам газа, конденсата и ГКФ.
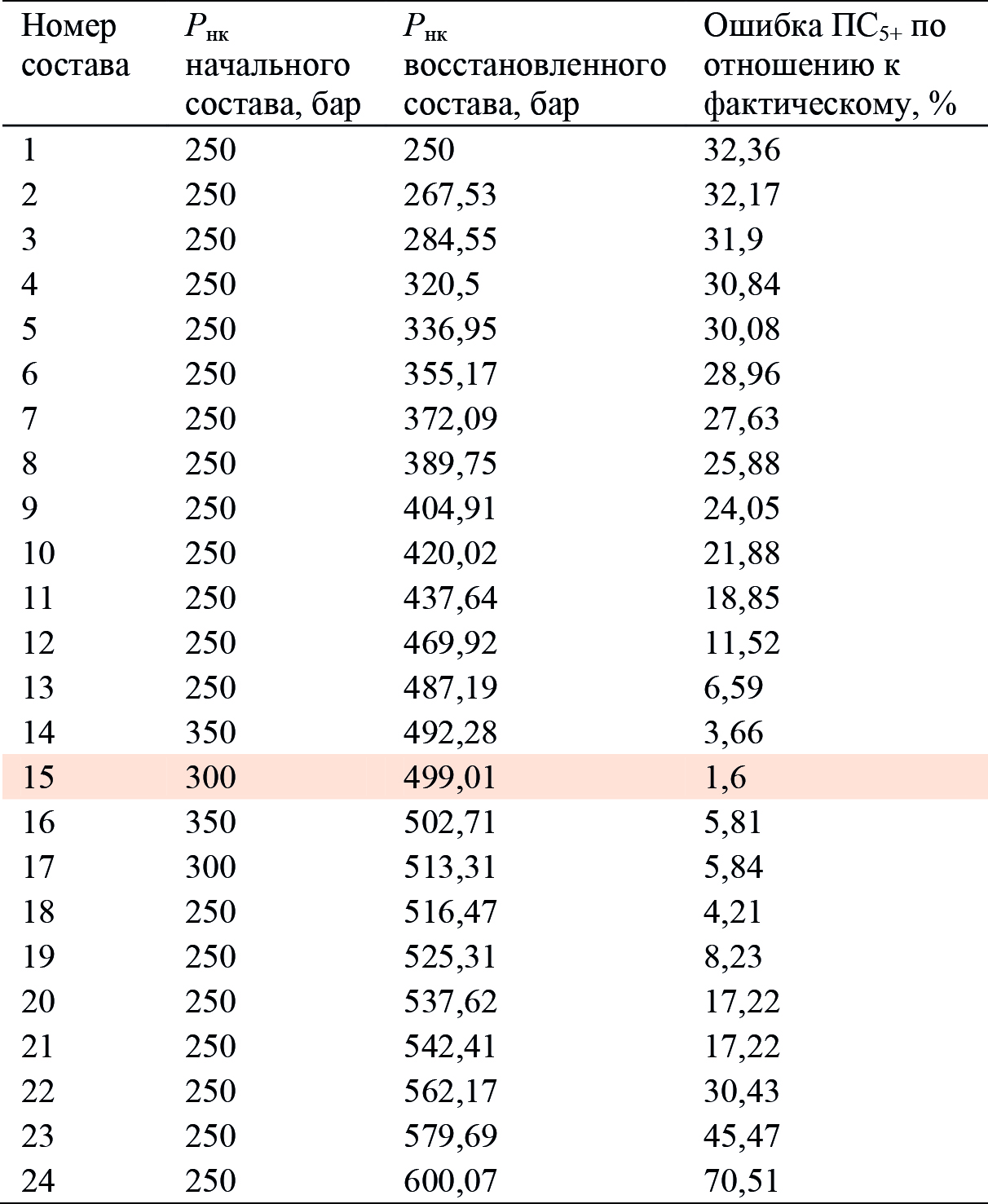
Табл. 5. Составы в соответствии с их Pнк и порядковым номером
при переборе в процессе решения обратной задачи (адаптации)
В результате численных экспериментов замечено, что модуль адаптации в программе tNavigator при минимизации любой из невязок выбирает состав с порядковым номером 15 (табл. 5), соответствующий Pнк = 499,01 бар (рис. 7). Отметим, что в данном случае варьируются только компонентные составы, а остальные параметры гидродинамической модели фиксируются.
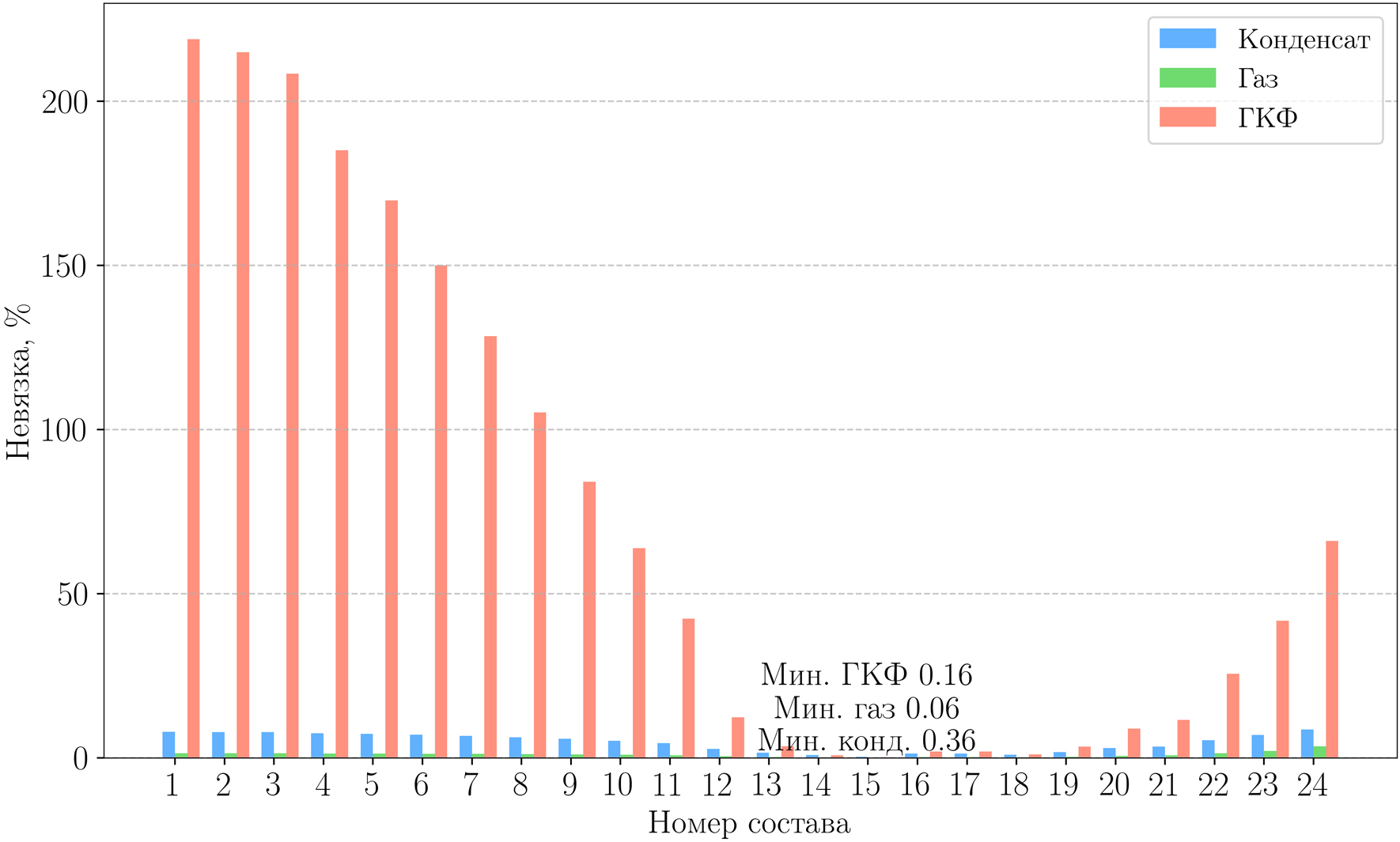
Рис. 7. Относительные невязки по дебиту газа, конденсата и ГКФ
для каждого из составов-кандидатов
Если дополнительно вычислить среднюю покомпонентную относительную ошибку по каждому из составов-кандидатов в сравнении с фактическим компонентным составом (рис. 8), то можно заметить, что модуль адаптации выбирает состав со сравнительно меньшим значением Pнк в качестве наиболее близкого к фактическому, у которого Pнк = 506,08 бар. Тем не менее с точки зрения метрики близости значения ПС5+ найденный состав является самым подходящим из приведенных.
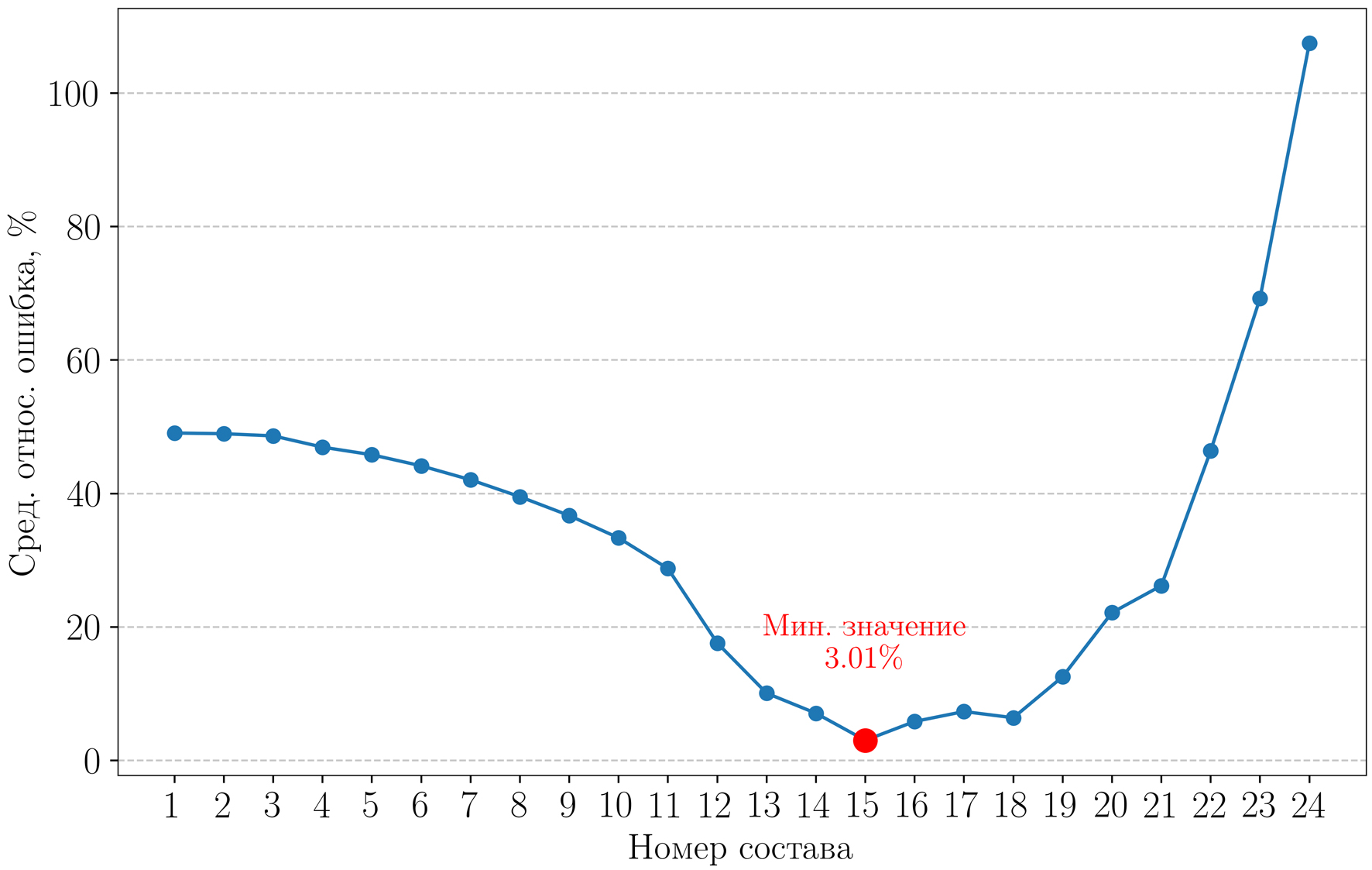
Рис. 8. Средняя покомпонентная относительная ошибка в процентах
относительно фактического состава для каждого из 24 составов
Отметим, что для применения методики возникают дополнительные требования к проведению ГКИ: подробная запись датчиков глубинного давления, полная запись показаний расходомеров по газу, замеров конденсата по сепаратору, определение плотностей газа и конденсата и т.д. Требования связаны с необходимостью наличия подробного набора данных для адаптации.
2.4 Анализ чувствительности решения обратной задачи к неопределенности в параметрах модели
Для анализа чувствительности решения обратной задачи к неопределенности в неварьируемых параметрах модели выбран метод «One at time». При таком подходе фиксируется некоторый срединный набор параметров ГД-модели и находится решение задачи, называемое срединным, а затем параметры варьируются в заданных пределах по одному за раз при фиксированных остальных и отслеживается степень изменения решения задачи относительно срединного решения. В данном случае используемые срединные значения параметров пласта, трещин ГРП и ОФП заданы в табл. 3, 4. Поскольку для этих фиксированных значений параметров решением обратной задачи является состав 15 (табл. 5) с Pнк = 499,01 бар, то состав 15 и будет считаться срединным композиционным составом.
В численных экспериментах каждый из параметров (табл. 3, 4) варьируется на 20% в большую и меньшую сторону за исключением проницаемости пласта. В силу особенностей данной неопределенности проницаемость изменяется от 0,05 до 1 мД.
Чувствительность решения обратной задачи к некоторому параметру предлагается определять по составу, который выбирается в качестве решения при изменении значения этого параметра, и численно оценить эту чувствительность можно по изменению величины ПС5+. Таким образом, для 14 приведенных параметров (табл. 3, 4) получается 28 численных экспериментов, проведенных в модуле адаптации tNavigator. Для каждого эксперимента запускается решение обратной задачи по нахождению компонентного состава перебором по сетке (24 состава из табл. 5).
Результаты решения обратной задачи при изменении параметров ГД-модели (внесение неопределенности) представлены в табл. 6, где приведены значения варьируемого параметра, невязки по дебиту газа, дебиту конденсата и ГКФ, а также номер выбираемого состава по каждой из невязок. Отсюда следует, что при наличии неопределенностей в параметрах задачи выбор невязки, по минимизации которой проводится выбор композиционного состава, имеет большое значение. Если, например, в качестве значения проницаемости взять 1 мД и целевой функцией задать невязку по дебиту конденсата, то после решения обратной задачи получим 1-й состав, а если целевой функцией взять невязку по дебиту газа, то определяется 24-й состав (рис. 9). Отметим, что оба выбираемые состава, и 1-й, и 24-й состав, имеют большую погрешность по ПС5+ в сравнении с фактическим составом (табл. 5, последний столбец).
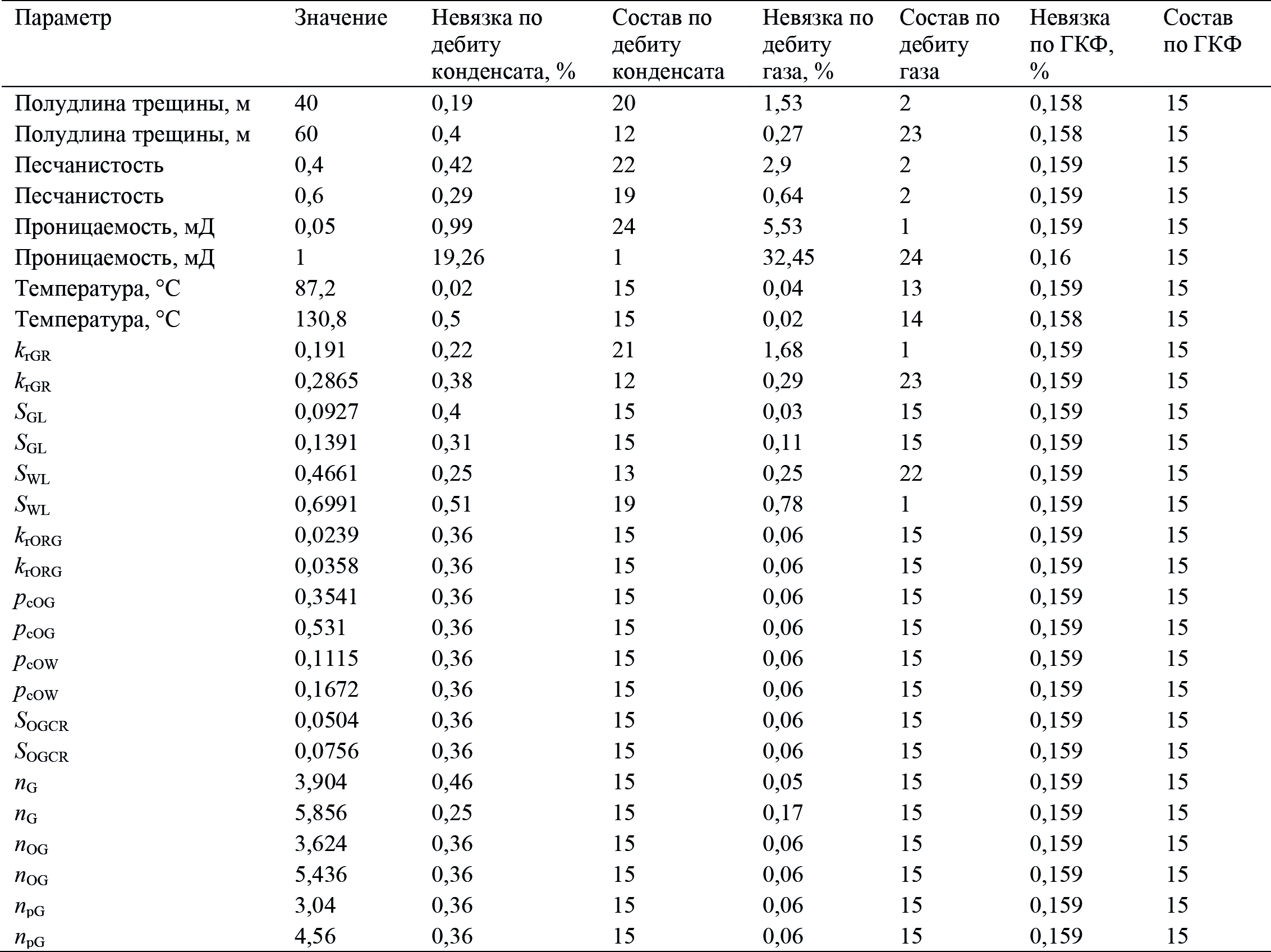
Табл. 6. Невязки по дебитам газа, конденсата, ГКФ и номера выбранных составов,
найденные при решении обратной задачи при изменении параметров ГД-модели
в рамках анализа чувствительности
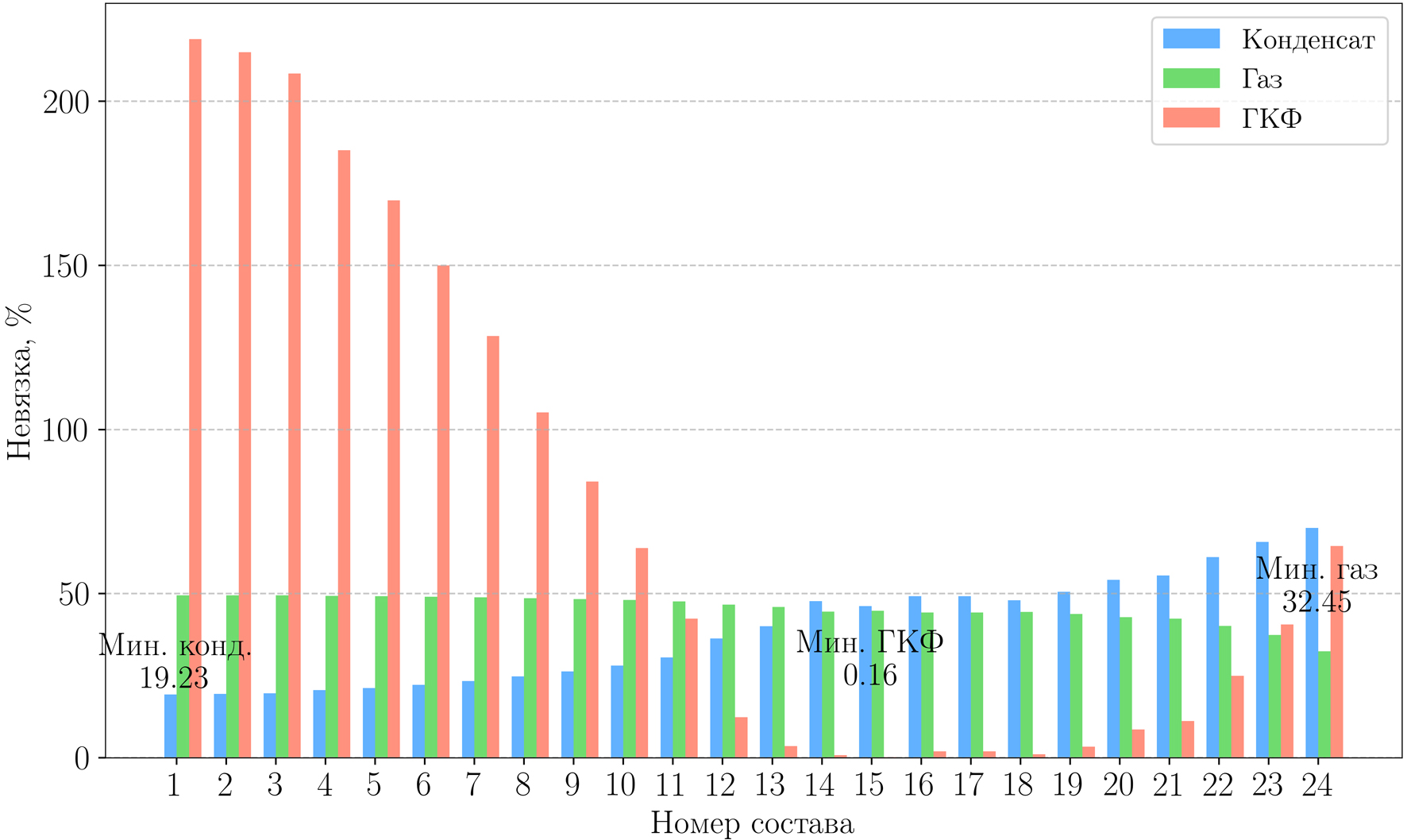
Рис. 9. Относительные невязки по дебиту газа, конденсата и ГКФ
для каждого из составов-кандидатов при значении проницаемости 1 мД в ГД-модели
Кроме того, анализ данных табл. 6 показывает, что решение обратной задачи (выбираемый состав) по дебитам газа и конденсата меняется при изменении таких параметров, как полудлина трещины ГРП, песчанистость, температура пласта и два параметра ОФП (минимальная насыщенность водой SWL и относительная фазовая проницаемость по газу при остаточной насыщенности конденсатом krGR). Изменение других параметров в указанных пределах не вносит ошибку в решение обратной задачи в том смысле, что выбирается срединный состав.
Следует подчеркнуть, что в качестве решения обратной задачи по невязке по ГКФ вне зависимости от значения варьируемого параметра выбирается один и тот же 15-й состав, который и является срединным. Таким образом, решение обратной задачи об определении компонентного состава по невязке по ГКФ является малочувствительным к изменению остальных параметров ГД-модели.
2.5 Влияние неопределенности в ГКФ на решение обратной задачи
Предположим, что в исторических значениях ГКФ есть погрешность в пределах 10%. Такая ситуация моделируется следующим образом. В фактические значения ГКФ искусственно вносится погрешность порядка ±10%, или, иными словами, ГКФ равномерно по всем временным точкам уменьшается или увеличивается на 10%. На основании фактических дебитов конденсата и измененного ГКФ пересчитываются фактические дебиты газа. Для таких измененных дебитов газа, дебитов конденсата и ГКФ при срединных параметрах ГД-модели (табл. 3, 4) запускается процесс подбора наиболее подходящего композиционного состава по минимизации невязки по ГКФ и получаются следующие результаты. Вместо 15-го состава модуль адаптации определяет либо 13-й, либо 19-й состав (табл. 7). При этом ошибка в ПС5+ по отношению ПС5+ фактического и срединного (15-го) составов составляет от 6% до 9%.

Табл. 7. Результаты решения обратной задачи о нахождении компонентного состава
при внесении погрешности фактического ГКФ в интервале ±10%
На рис. 10 приведены относительные покомпонентные ошибки выбираемых 13-го и 19-го составов, а также срединного 15-го по отношению к фактическому. Углеводородные компоненты упорядочены по возрастанию карбонового числа. Из гистограммы на рис. 10 следует, что ошибка в определении ГКФ приводит либо к завышенной, либо к заниженной оценке содержания тяжелых компонент. Отметим, что для углеводородных компонент с С1 по С14 покомпонентные ошибки обоих составов (13-й и 19-й) не превышают 7%, а ошибка для более тяжелых компонент может превышать 25%. При этом суммарное мольное содержание в процентах углеводородных компонент с iС5 по С14 для фактического, 15-го, 13-го и 19-го составов имеют близкие значения, равные 2,59%, 2,64%, 2,54% и 2,68% соответственно. Суммарные мольные доли оставшихся тяжелых углеводородных компонент (с С15 по С42–С50) не превышают 0,5% и ошибки в определении содержания этих компонент в составах не приводят к значительным ошибкам в оценке ПС5+.
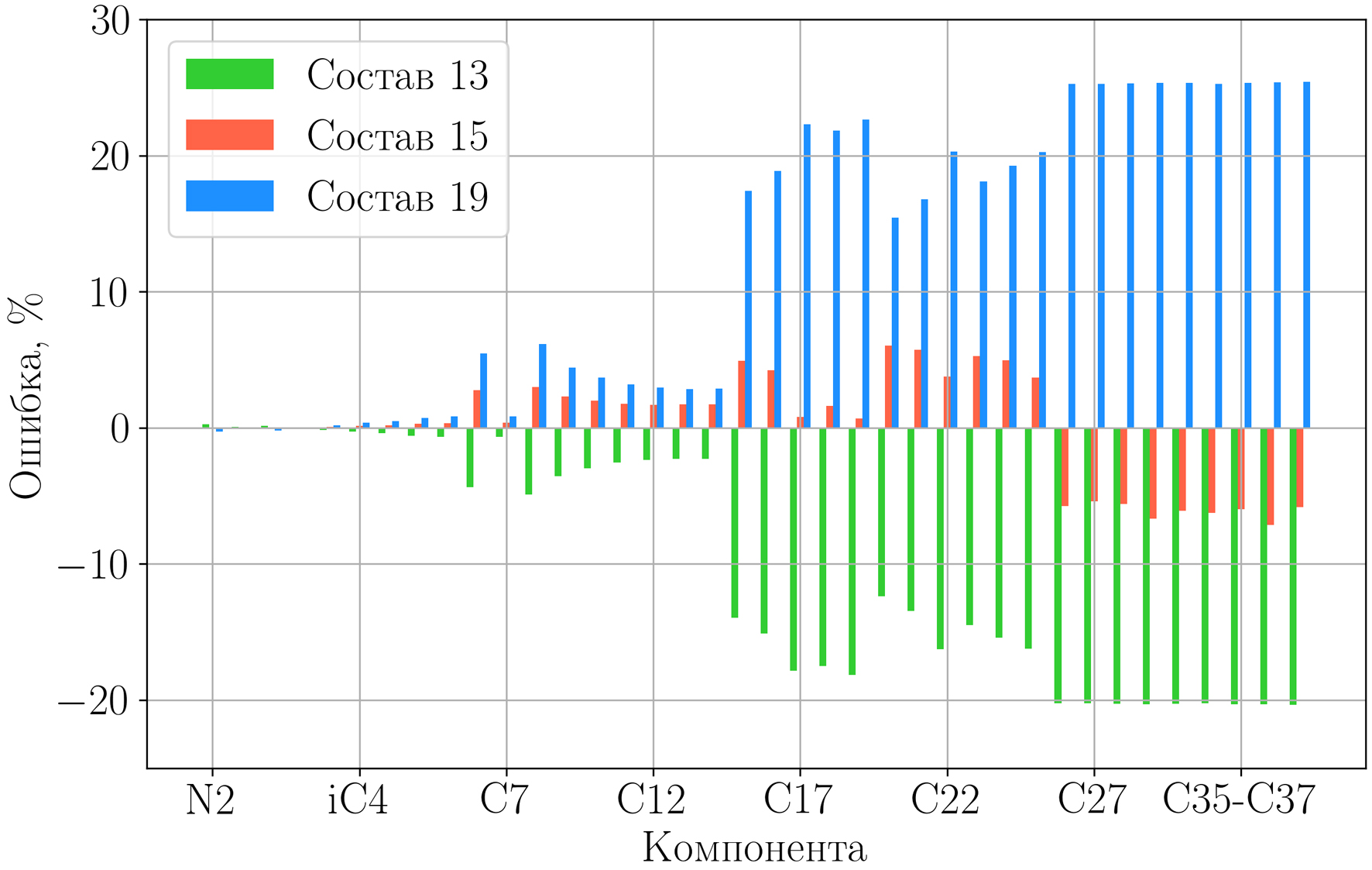
Рис. 10. Относительные ошибки мольного содержания компонент в процентах
для 13-го, 15-го и 19-го составов по отношению к фактическому составу
2.6 Применение методики к реальным данным
На основании проведенного анализа чувствительности решения обратной задачи на синтетических данных (п. 2.5) можно сделать вывод, что при наличии существенных неопределенностей в основных параметрах модели уточнение компонентного состава нельзя проводить по невязкам дебитов конденсата или газа. Кроме того, оказывается, что ГКФ малочувствителен к изменениям основных параметров ГД-модели, что позволяет корректно определять компонентный состав вне зависимости от неопределенности в параметрах пласта, трещин и ОФП.
Таким образом, задачу подбора параметров ГД-модели при наличии неопределенности в композиционном составе пластового флюида предлагается разделить на две независимые подзадачи:
1) первоначальный подбор композиционного состава путем минимизации невязки по ГКФ из предварительно созданного набора составов, полученных донасыщением некоторого начального газа тяжелыми компонентами;
2) последующий подбор остальных параметров ГД-модели по дебитам газа и/или конденсата при фиксированном найденном на предыдущем шаге композиционном составе.
Предложенная методика апробирована на промысловых данных, полученных при исследовании скважины Х27 с горизонтальным окончанием месторождения X. Для рассматриваемой скважины отсутствовала точная информация об основных параметрах пласта, трещин ГРП, ОФП и состава газоконденсатной смеси. На практике в таких случаях используют данные скважин-аналогов и композиционные составы-аналоги. Составом-аналогом для Х27 является состав, приведенный в табл. 1, а параметры скважин-аналогов приведены в табл. 3, 4.
Данные, собранные в ходе ГКИ, включают значения устьевых давлений, дебитов газа, измеренных с помощью расходомера, дебитов стабильного конденсата, замеренных по сепаратору. Пластовое давление для Х27 оценивается в 600 бар, а давление на забое пересчитывается по устьевым давлениям. Из данных по давлению исключены аномальные значения и выбросы и выделены четыре режима работы скважины в ходе ГКИ, которые отражены на рис. 11.
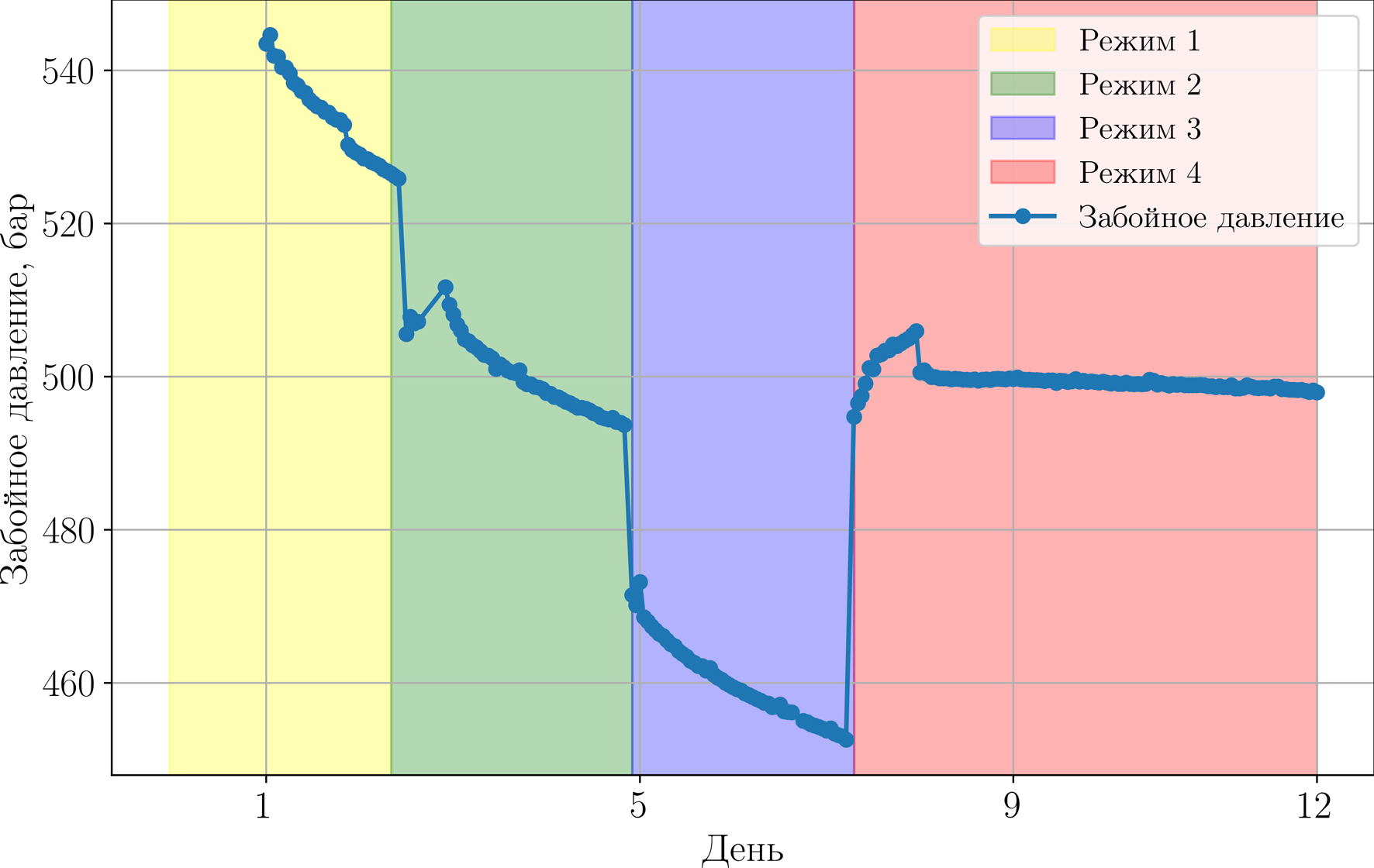
Рис. 11. Зависимость забойного давления от времени для скважины X27
при проведении ГКИ
Для расчета прямой задачи используется ГД-модель, аналогичная построенной в п. 2.3.1, в которой число трещин ГРП увеличено до 9 и реализован режим изменения забойного давления в соответствии с графиком на рис. 11. Кроме того, в модели установлены параметры двухступенчатого сепаратора для дальнейшего пересчета дебитов при заданных термобарических условиях. Давление и температура первой ступени сепаратора на каждом из четырех режимов задается согласно ГЖ, вторая ступень сепаратора соответствует стандартным условиям (давление 1,01325 бар, температура 20 °С). В качестве фактического исторического ГКФ принимается отношение дебитов газа по расходомеру в м3 и стабильного конденсата по сепаратору в м3, приведенных в стандартные условия.
Такая модель способствует более реалистичному описанию процессов и позволяет учитывать специфику каждого режима отдельно. Однако следует отметить, что рассматривается упрощенная постановка, поскольку моделируется одиночная скважина в однородном пласте и предполагается, что в начальный момент времени в пласте находится однофазный флюид – газ. Давление в пласте начинает падать за счет отбора флюида только после запуска скважины с первого режима.
В силу широкой неопределенности по давлению начала конденсации пластового флюида число составов (табл. 5) расширено до 39 (табл. 8) так, чтобы Pнк не только покрывало широкий диапазон значений от 250 бар до пластового, равного 600 бар, но и присутствовала вариативность компонентного состава.
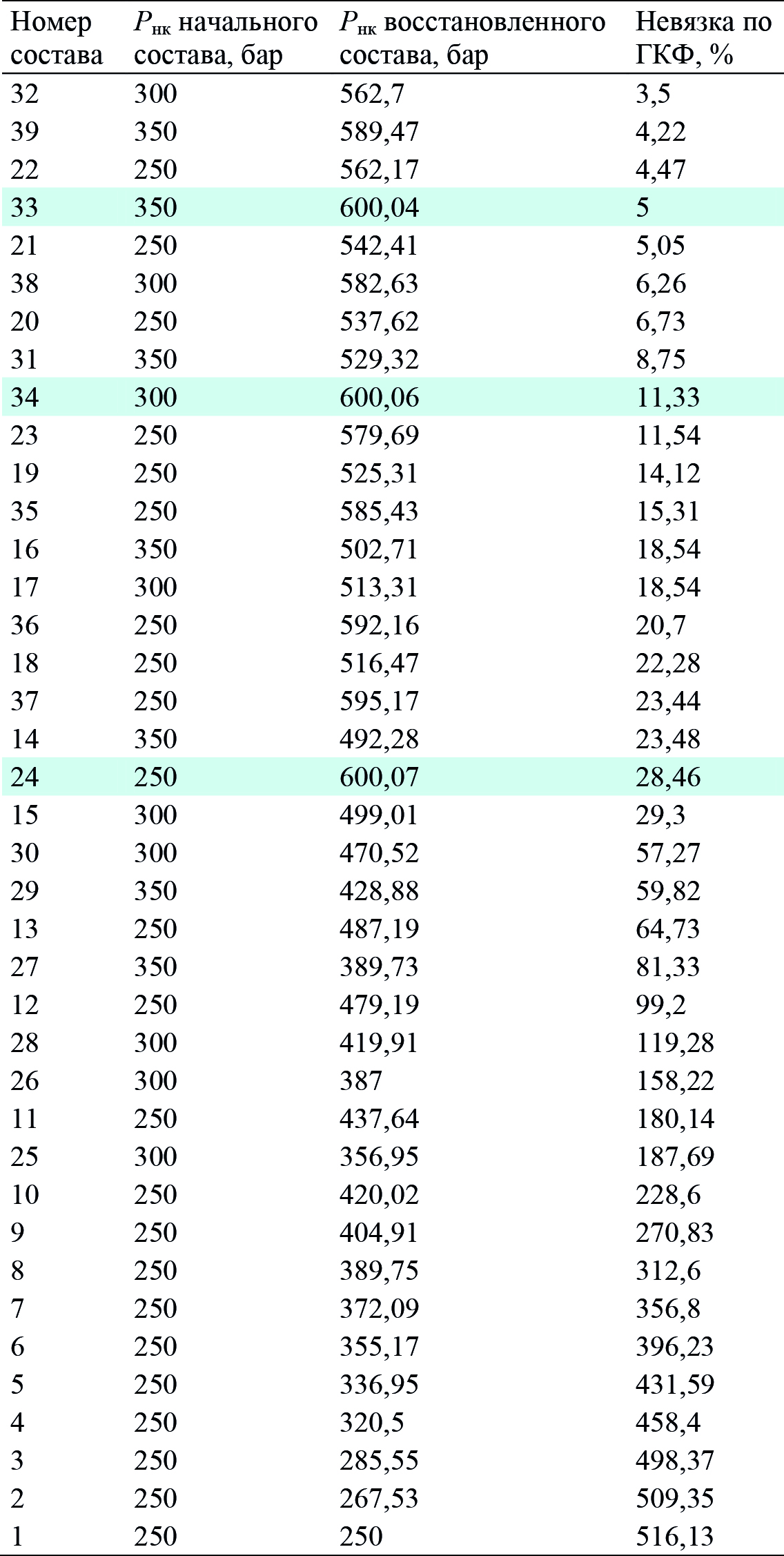
Табл. 8. Восстановленные составы и результаты работы модуля адаптации
при апробации разработанной методики на реальных данных
На рис. 12 приведены реальные показатели ГКФ по ГКИ, которые отмечены черными точками, и профили ГКФ по расчету на ГД-модели для некоторых составов из табл. 8. Следует отметить зависимость ГКФ от композиционного состава. Так, например, 24-й и 33-й составы, восстановленные из начальных составов с Pнк 250 и 350 бар соответственно, имеют Pнк, близкое к 600 бар, но при этом у них различное мольное содержание тяжелых компонент, и они дают разные значения ГКФ.
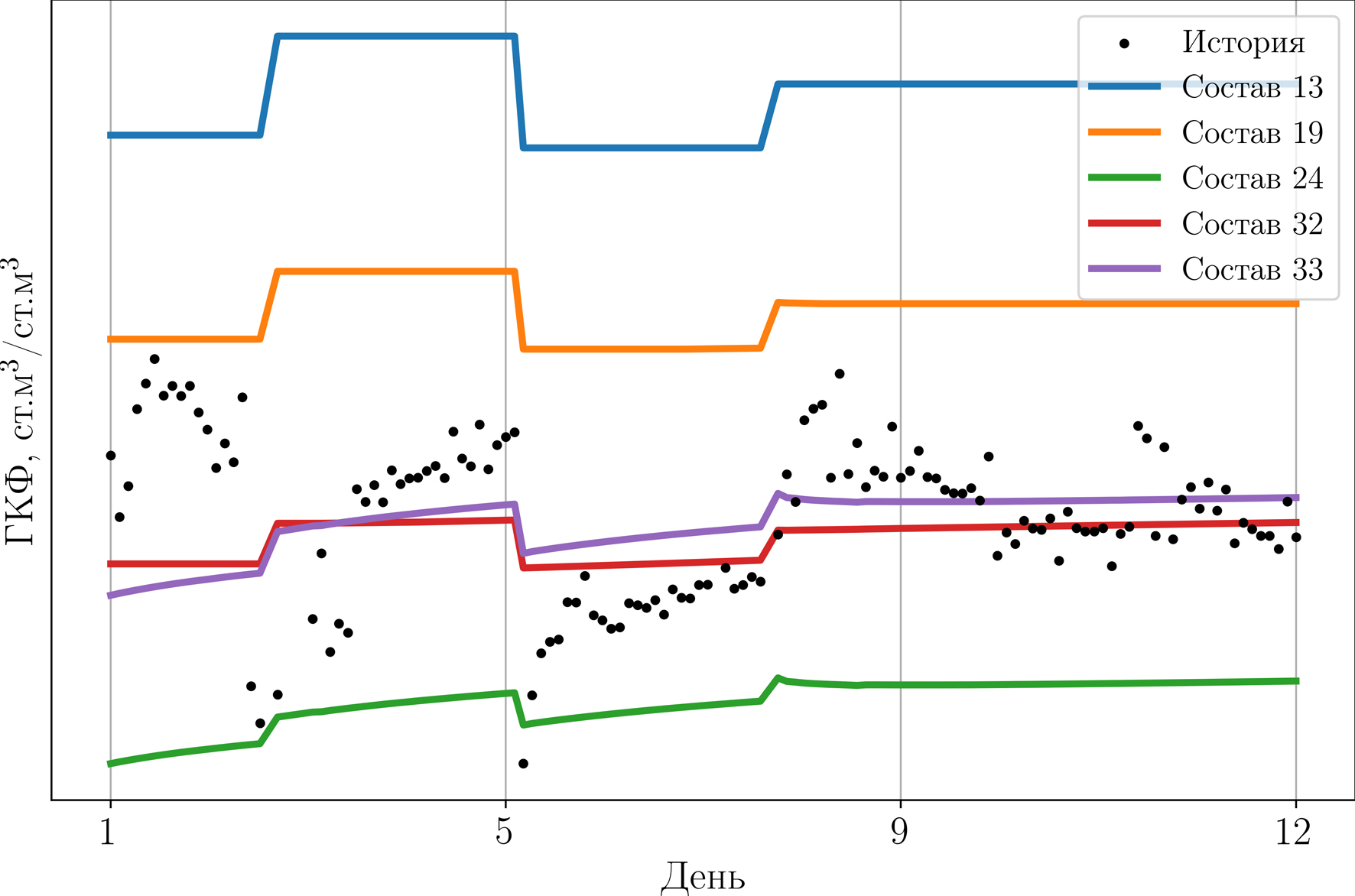
Рис. 12. Реальные данные ГКФ по ГЖ и расчетам по ГД-модели для различных составов
Далее решается обратная задача подбора наиболее подходящего композиционного состава по данным ГКФ с использованием модуля адаптации tNavigator. Результаты работы модуля демонстрируются в табл. 8, где приведены номер состава, давление начала конденсации начального состава, от которого он был восстановлен, Pнк состава, невязка по ГКФ. В результате по наименьшей невязке ГКФ выбирается 32-й состав как наилучший. Однако в силу малой величины невязки составы с номерами 39, 22, 33 и 21 также могут считаться подходящими составами. Отклонение по значениям ПС5+ этих составов от лучшего 32-го состава составляет 5,8%, 3,4%, 9,4% и 6.3% соответственно. Поскольку погрешность не превышает 10%, на практике для реального месторождения это считается приемлемой погрешностью. Для производственных задач, требующих большей точности, необходимо подбирать оборудование и планировать ГКИ так, чтобы обеспечить высокую точность измерения дебита газа и конденсата.
В дальнейшем 32-й композиционный состав, выбранный в качестве лучшего, фиксируется и проводится подбор основных параметров ГД-модели с помощью минимизации разницы между модельными и реальными данными по дебитам из ГЖ. Начальные значения параметров ГД-модели задаются в соответствии с табл. 3, 4. Подбор параметров ГД-модели проводится с использованием метода поверхности отклика из модуля адаптации симулятора tNavigator, при этом в качестве целевой функции выбирается невязка по дебиту газа. Согласно проведенным расчетам метод поверхности отклика сходится за 1377 вычислений целевой функции с финальными невязками по дебиту газа, дебиту конденсата и ГКФ, равными 0,7%, 1,72% и 3.5% соответственно. Конечные результаты подбора параметров ГД-модели представлены в табл. 9.
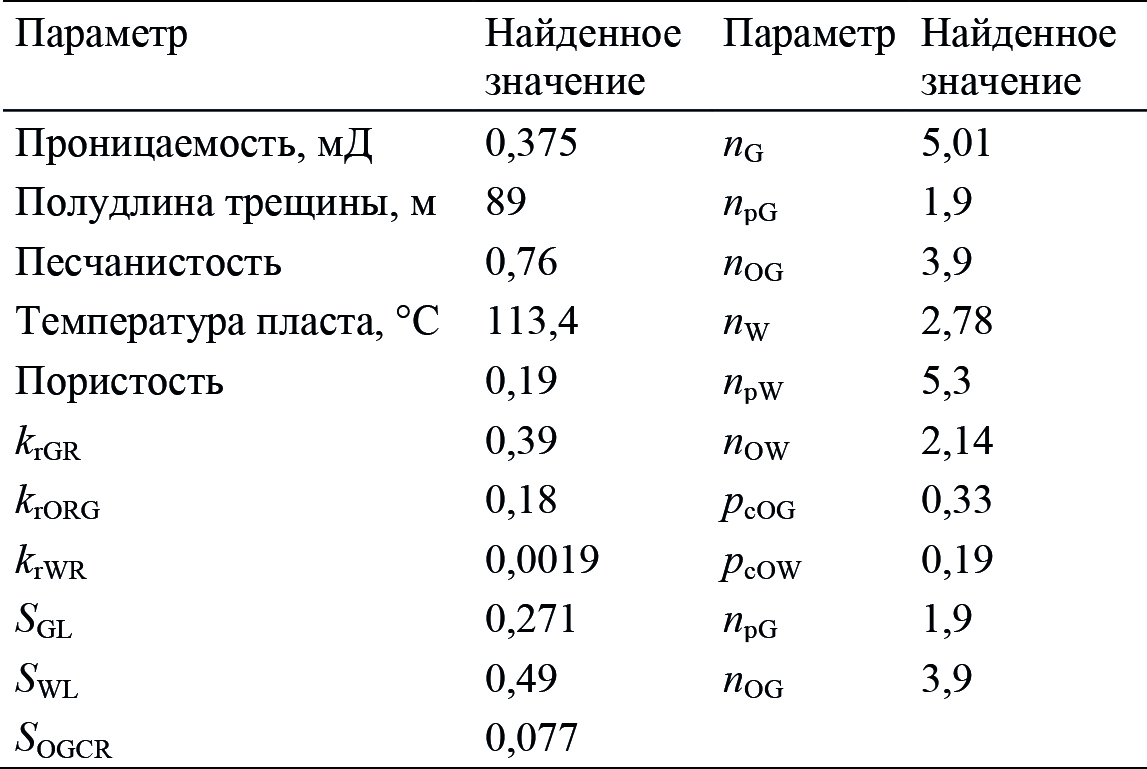
Табл. 9. Полученные значения параметров ГД-модели
при решении обратной задачи при адаптации на реальные данные дебитов
На рис. 13–15 в качестве иллюстрации представлена работа оптимизационного алгоритма, где показаны профили дебитов конденсата, газа и ГКФ соответственно, полученные при подборе параметров ГД-модели. Отметим хорошее качественное согласование расчетных профилей добычи конденсата и газа с данными ГЖ. Подчеркнем также, что в процессе адаптации считается средняя невязка по всему массиву временных точек. Поэтому, несмотря на небольшие значения невязок в целом, для первого режима наблюдается самое большое расхождение с историческими данными как для дебитов газа и конденсата, так и для ГКФ. Лучше всего согласуется последний, 4-й режим. Такое поведение можно объяснить ограничениями нашей ГД-модели, в которой рассматриваются однородный пласт и однофазный флюид в начальный момент времени, используются достаточно большие размеры ячейки вокруг трещин и скважины (10 м), а также не проводится аккуратное моделирование течения в скважине. Все это, возможно, не позволяет в том числе описать резкие скачки ГКФ при смене режима. Не исключены также погрешности замера дебита конденсата на сепараторе.
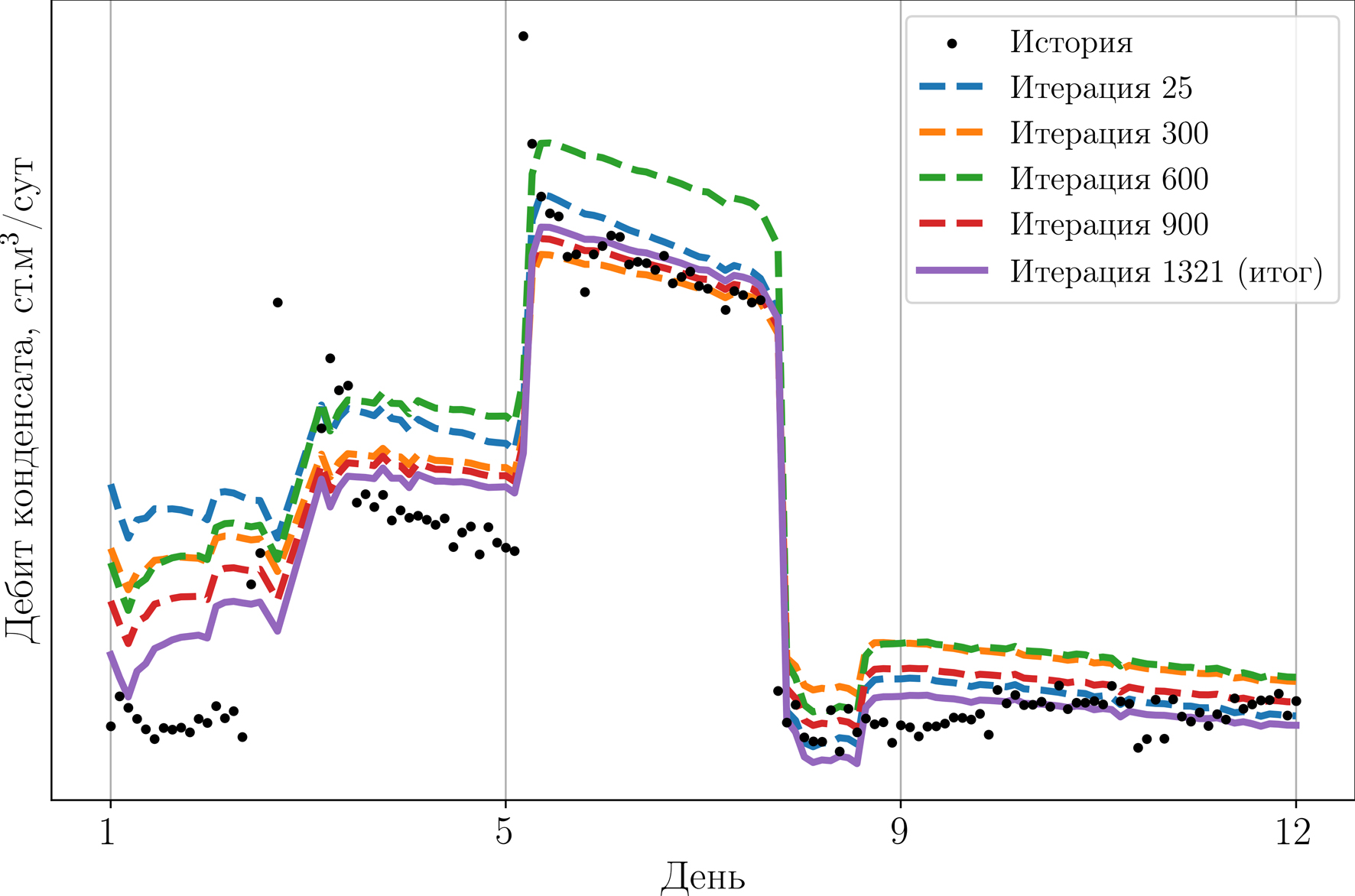
Рис. 13. Сравнение реальных дебитов конденсата по ГЖ (черные точки)
и полученных в ходе подбора параметров ГД-модели
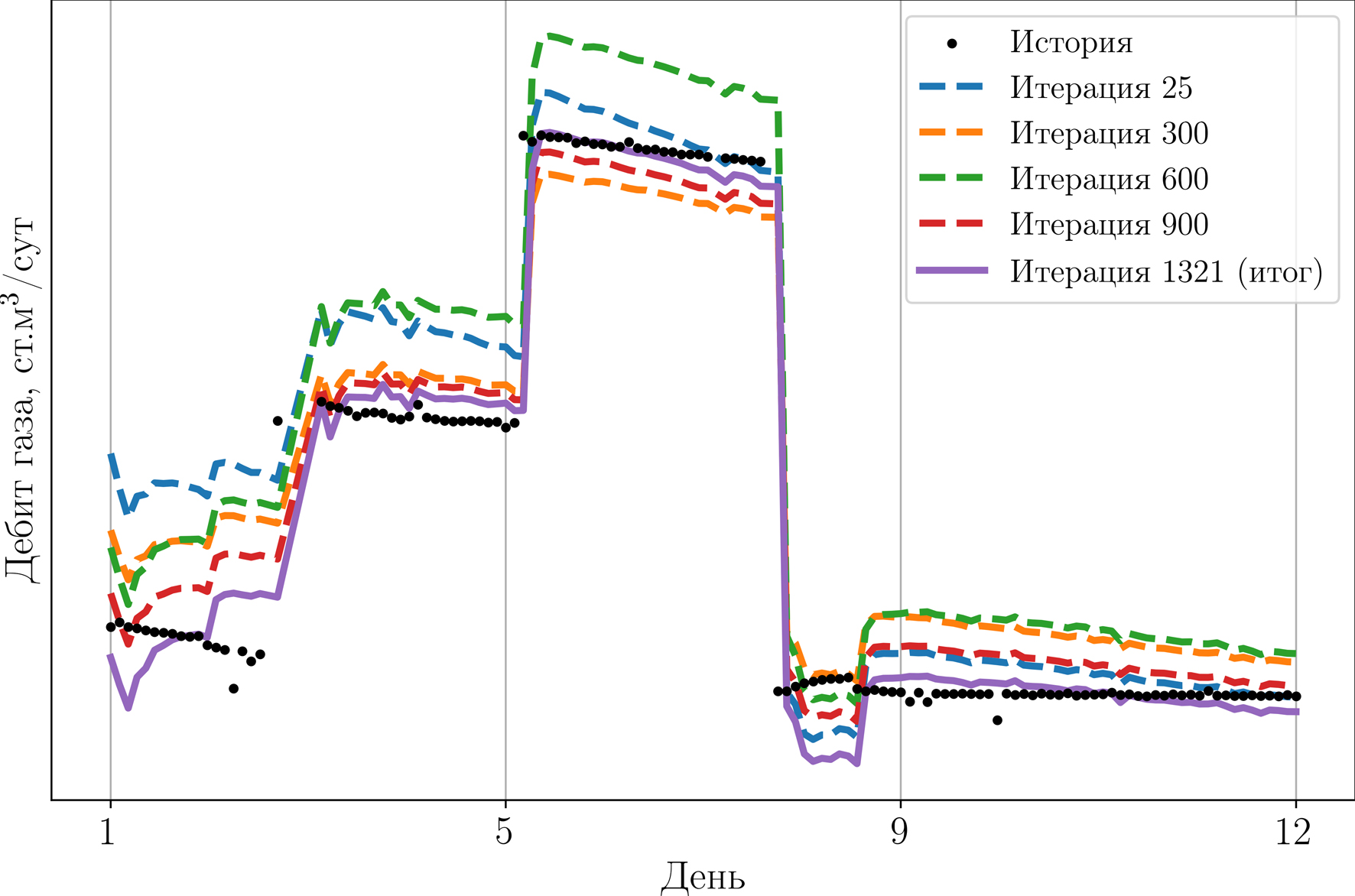
Рис. 14. Сравнение реальных дебитов газа по ГЖ (черные точки)
и полученных в ходе подбора параметров ГД-модели
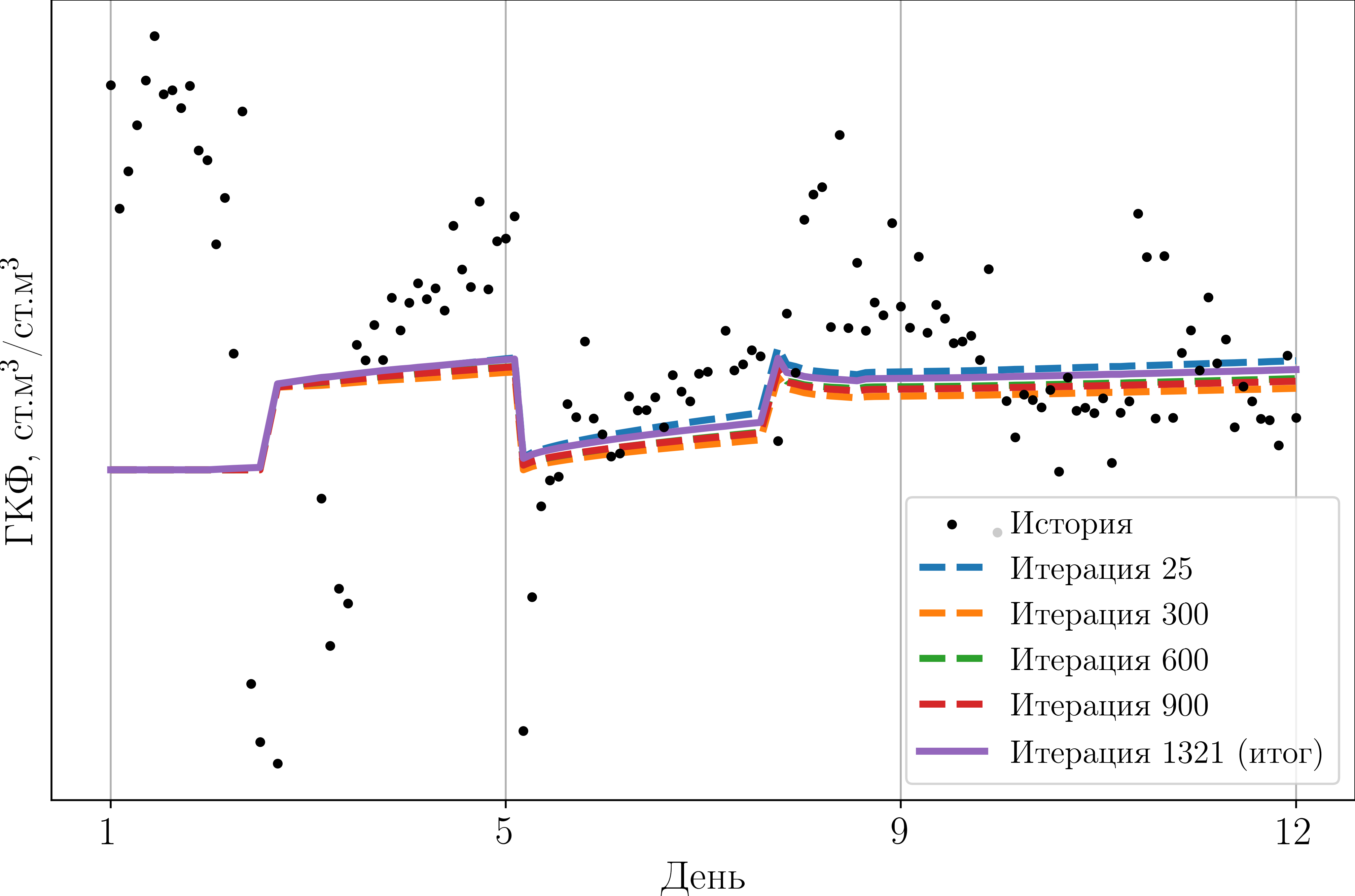
Рис. 15. Сравнение реальных данных по ГКФ из ГЖ (черные точки)
и полученных в ходе подбора параметров ГД-модели
Заключение
В работе предложена и проанализирована методика численного донасыщения обедненного газа тяжелыми компонентами, которая позволила на модельных данных воспроизвести исходный состав после его искусственного обеднения.
На основе данного способа донасыщения с использованием симулятора tNavigator для решения прямой задачи многофазной многокомпонентной фильтрации в пласте получено решение обратной задачи об определении компонентного состава ГКС в предположении, что все остальные параметры модели известны. В качестве целевой функции для минимизации при решении обратной задачи рассмотрены отклонения (невязки) модельных значений дебитов газа, дебитов конденсата и их отношения (ГКФ) от фактических полевых данных. При анализе решения на синтетических данных показано, что состав может быть определен путем минимизации любой из целевых функций.
В рамках исследования корректности обратной задачи проанализировано влияние неопределенностей в параметрах гидродинамической модели на решение обратной задачи об определении компонентного состава. Решение обратной задачи оказывается наименее чувствительным к варьированию параметров при использовании невязки по ГКФ как целевой функции. Показано также, что данное решение является устойчивым к неопределенности в значениях ГКФ. Если же проводить минимизацию невязки по дебитам газа или конденсата, то решение обратной задачи сильно зависит от параметров гидродинамической модели.
На основании проведенного анализа чувствительности предложен способ одновременного определения компонентного состава и основных параметров гидродинамической модели с помощью разделения на две подзадачи. Сначала решается обратная задача для поиска лучшего состава по невязке по ГКФ из набора составов, полученных на основе численных методик восстановления обедненного газа. Далее осуществляется подбор основных параметров пласта в гидродинамической модели на основе невязок конденсата и/или газа при фиксированном наилучшем составе.
Применение этой методики к реальной скважине, для которой предоставлены промысловые данные, позволяет выбрать наиболее подходящий компонентный состав и получить приемлемую невязку по дебитам газа и конденсата.
Таким образом, предложенный комплексный подход позволяет до проведения газоконденсатных исследований оценивать репрезентативность отобранных проб, в том числе для случаев, когда отбор кондиционных проб невозможен, запланировать дополнительные исследования для восстановления свойств и состава начального пластового газа.
Финансирование/Благодарности
Работа выполнена при поддержке Передовой инженерной школы НГУ и Научно-образовательного центра «Газпромнефть-НГУ». Вклад А.Н. Байкина поддержан стипендией Президента РФ (грант № СП-1703.2022.1). Коллектив авторов выражает благодарность компании Рок Флоу Динамикс за предоставление академической лицензии симулятора tNavigator.
Список литературы
1. Брусиловский А., Промзелев И. (2013). О методических подходах к уточнению PVT-свойств пластовой нефти двухфазных залежей. Вести газовой науки, 12(1), c. 41–45.
2. Брусиловский А., Ющенко Т. (2016). Научно обоснованный инженерный метод определения компонентного состава и PVT свойств пластовых углеводородных смесей при неполной исходной информации. PROНЕФТЬ. Профессионально о нефти, (1), c. 68–74.
3. ГОС Т Р 57851.4–2017. (2017). Смесь газоконденсатная. Часть 4. Расчет компонентно-фракционного состава. М.: Стандартинформ, 46 с.
4. Коротаев Ю.П., Ширковский А.И. (1984). Добыча, транспорт и подземное хранение газа. М.: Недра, 486 с.
5. Лапшин В.И., Посевич А.Г., Константинов А.А., Волков А.Н. (2019). Особенности определения газоконденсатных характеристик при освоении глубокозалегающих месторождений с большой продуктивной толщей. Вести газовой науки, 38(1), с. 29–40.
6. Р-Газпром 086-2010. (2011). Инструкция по комплексным исследованиям газовых и газоконденсатных скважин: в 2 ч. М.: ООО «Газпром экспо».
7. Bonyadi M., Esmaeilzadeh F., Mowla D., Nematollahi M. (2014). Theoretical and experimental determination of initial reservoir fluid in a lean gas condensate reservoir. Journal of Petroleum Science and Engineering, 114, pp. 74–81. https://doi.org/10.1016/j.petrol.2014.01.003
8. Elsharkawy A.M. (2002). Predicting the dew point pressure for gas condensate reservoirs: empirical models and equations of state. Fluid Phase Equilibria, 193(1–2), pp. 147–165. https://doi.org/10.1016/S0378-3812(01)00724-5
9. Fevang Ø., Whitson C.H. (1994). Accurate insitu compositions in petroleum reservoirs. European Petroleum Conference, SPE-28829-MS. https://doi.org/10.2118/28829-MS
10. Myron B.A. (2021).The Mathematics of Fluid Flow Through Porous Media. Wiley, 224 p. https://doi.org/10.1002/9781119663881
11. Osfouri S., Azin R. (2016). An overview of challenges and errors in sampling and recombination of gas condensate fluids. Journal of Oil, Gas and Petrochemical Technology, 3(1), pp. 1–14. https://doi.org/10.22034/jogpt.2016.43155
12. Promzelev I., Brusilovsky A., Kuporosov D., Yushchenko T. (2018). Peculiarities of Identification of Reservoir Fluids Properties of Two-Phase With Oil Rim and Gas Cap Deposits: From Sampling to Justification of the Parameters for Calculating Reserves and PVT Data for Hydrodynamic Simulation of Field Development. SPE Russian Petroleum Technology Conference, SPE-191566-18RPTC-MS. https://doi.org/10.2118/191566-18RPTC-MS
13. Reffstrup J., Olsen H. (1994) Evaluation of PVT data from low permeability gas condensate reservoirs. North Sea Oil and Gas Reservoirs – III. Ed. by J.O. Aasen, E. Berg, A.T. Buller, O. Hjelmeland, R.M. Holt, J. Kleppe, O. Torsæter. Dordrecht: Springer, pp. 289–296. https://doi.org/10.1007/978-94-011-0896-6_25
14. Schebetov A., Rimoldi A., Piana M. (2010). Quality check of gascondensate PVT studies and EOS modelling under input data uncertainty. SPE Russian Oil and Gas Conference and Exhibition, SPE-133258-MS. https://doi.org/10.2118/133258-MS
15. tNavigator 23.1. (2023). Симулятор. Техническое руководство, RFD: Rock Flow Dynamics, 3855 c.
16. Turner R.G., Hubbard M.G., Dukler A.E. (1969). Analysis and Prediction of Minimum Flow Rate for the Continuous Removal of Liquids from Gas Wells. Journal of Petrol Technology, 21(11), pp. 1475–1482. https://doi.org/10.2118/2198-PA
17. Yang Y., Wang H., Lun Z., Hu W. (2020). A new method to calculate the in-situ compositions of gas condensate reservoirs. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, pp. 1–13. https://doi.org/10.1080/15567036.2020.1827093
Об авторах
А. А. ГимазовРоссия
Азат Альбертович Гимазов – кандидат физ.-мат. наук, руководитель программ, Центр компетенций по газовым проектам
190000, Санкт-Петербург, Набережная реки Мойки, д. 75–79
Б. Х. Имомназаров
Россия
Бунед Холматжонович Имомназаров – младший научный сотрудник
630090, Новосибирск, пр. Ак. Лаврентьева, д. 15
Б. Н. Старовойтова
Россия
Ботагоз Николаевна Старовойтова – кандидат физ.мат. наук, научный сотрудник
630090, Новосибирск, пр. Ак. Лаврентьева, д. 15
А. Н. Байкин
Россия
Алексей Николаевич Байкин – кандидат физ.-мат. наук, старший научный сотрудник
630090, Новосибирск, пр. Ак. Лаврентьева, д. 15
В. М. Бабин
Россия
Владимир Маркович Бабин – эксперт
190000, Санкт-Петербург, Набережная реки Мойки, д. 75–79
Д. Ф. Хамидуллин
Россия
Денис Фанилевич Хамидуллин – ведущий специалист, Центр компетенций по газовым проектам
190000, Санкт-Петербург, Набережная реки Мойки, д. 75–79
Д. Н. Купоросов
Россия
Дмитрий Николаевич Купоросов – начальник отдела
190000, Санкт-Петербург, Набережная реки Мойки, д. 75–79
Рецензия
Для цитирования:
Гимазов А.А., Имомназаров Б.Х., Старовойтова Б.Н., Байкин А.Н., Бабин В.М., Хамидуллин Д.Ф., Купоросов Д.Н. Решение обратной задачи определения начального компонентного состава углеводородов газоконденсатного месторождения по известным промысловым данным. Георесурсы. 2024;26(3):73-86. https://doi.org/10.18599/grs.2024.3.9
For citation:
Gimazov A.М., Imomnazarov B.Kh., Starovoytova B.N., Baykin A.N., Babin V.M., Khamidullin D.F., Kuporosov D.N. Solution of the Inverse Problem of Determining the Initial Hydrocarbons Composition in a Gas-Condensate Reservoir Using Field Data. Georesursy = Georesources. 2024;26(3):73-86. (In Russ.) https://doi.org/10.18599/grs.2024.3.9















.png)


