Перейти к:
Определение удельного электрического сопротивления керна с помощью тороидальных катушек: математическое моделирование
https://doi.org/10.18599/grs.2024.3.16
Аннотация
Рассмотрена возможность определения удельного электрического сопротивления (УЭС) цилиндрического керна с помощью размещённой вокруг него генераторно-измерительной системы с тороидальными катушками. Разработан и верифицирован алгоритм двумерного конечно-разностного моделирования электрических и магнитных сигналов от стороннего кругового магнитного гармонического тока, эквивалентного тороидальной катушке. Выполнено двумерное численное моделирование реальной (синфазной) и мнимой (противофазной) составляющих вертикальной компоненты электрического поля и тангенциальной компоненты магнитного поля для практически значимого диапазона УЭС керна, когда образец находится в изолирующей или сильнопроводящей трубе с тороидальными катушками. По результатам численного моделирования выбраны оптимальная длина измерительной системы, а также операционная частота и тип измеряемых сигналов. Предложена трансформация последних в значения кажущихся УЭС вертикально-неоднородных образцов. Установлены критерии соответствия измеряемых сигналов в тонкослоистых и эквивалентных электрически-макроанизотропных образцах при изменении электрического контраста и толщины прослоев.
Ключевые слова
Для цитирования:
Эпов М.И., Мамяшев В.Г., Михайлов И.В., Суродина И.В., Никитенко М.Н. Определение удельного электрического сопротивления керна с помощью тороидальных катушек: математическое моделирование. Георесурсы. 2024;26(3):151-161. https://doi.org/10.18599/grs.2024.3.16
For citation:
Epov M.I., Mamyashev V.G., Mikhaylov I.V., Surodina I.V., Nikitenko M.N. Application of Toroidal Coils to Obtain Electrical Resistivity of Core Samples: Mathematical Modeling. Georesursy = Georesources. 2024;26(3):151-161. (In Russ.) https://doi.org/10.18599/grs.2024.3.16
Введение
В настоящее время в мировой практике для лабораторных исследований кернового материала используются различные методы и подходы для определения его петрофизических свойств. Широко применяются термические методы (Фадеева и др., 2020; Ahmed et al., 2021; Luc Leroy et al., 2021) с оценкой влияния температуры образца на его геомеханические свойства (Ashrafi et al., 2020; Gu et al., 2020). Постоянно исследуются сейсмические параметры керна (Kästner et al., 2020; Kästner et al., 2022) и их взаимосвязи с геомеханическими параметрами (Sharifi et al., 2023). Активно развивается направление ЯМР-релаксометрии c оперативным получением количественной информации о структуре порового пространства, распределении фильтрационно-емкостных свойств и типе насыщающего флюида (Шумскайте и др., 2022; Shumskayte et al., 2022; Elsayed et al., 2022).
Одно из наиболее динамичных направлений связано с цифровыми кернами, при построении которых применяются методы сканирующей электронной микроскопии и рентгеновской микротомографии. В ряде случаев необходимо сочетать данные этих двух методов – для получения информации о морфологии пустотного пространства, которую затруднительно идентифицировать только по микротомографии (Ponomarev et al., 2024). По цифровому керну можно определить широкий спектр его петрофизических характеристик: это эффективная электропроводность (Хачкова и др., 2020; Эпов и др., 2023); акустическая эмиссия (Решетова, Анчугов, 2021); многофазная фильтрация (Герке и др., 2021); абсолютная проницаемость (Хачкова и др., 2023).
Отдельно отметим группу методов электрометрии, которые являются основными для последующей оценки коэффициента нефтегазонасыщения горных пород. Удельное электрическое сопротивление (УЭС) керна может определяться из измерений как многочастотными электродными системами (Li et al., 2019; Kim et al., 2021), так и индукционными (Ben Aoun et al., 2018). Широкое распространение также получила диэлькометрия (Мезин и др., 2020) с получением комплексной диэлектрической проницаемости и оценкой ее частотной дисперсии (Liu et al., 2016; Morte, Hascakir, 2019).
Несмотря на отмеченное разнообразие методов исследования петрофизических свойств керна, не раскрытым в научно-практическом плане потенциалом обладают и другие подходы. Так, например, пространственное распределение УЭС в керне может изучаться с использованием других источников и приемников электромагнитного поля, например тороидальных катушек. Особенности электромагнитного поля тороидальной катушки теоретически исследованы и обобщены в работе (Каринский, 2018). Значительное число публикаций посвящено анализу сигналов каротажных зондов с тороидальными катушками для решения задач нефтепромысловой геофизики. Применительно к изучению кернового материала результаты таких исследований, по имеющейся у нас информации, не представлены в открытой печати. Настоящая работа посвящена исследованию возможностей систем с генераторной и измерительной тороидальными катушками для определения УЭС образцов керна методами математического и численного моделирования. Предполагается, что определение УЭС выполняется в скважине на образце только что выбуренного керна либо при лабораторных измерениях.
Математическая постановка
Рассмотрим модель цилиндрического образца керна радиуса a и длины L. Образец осесимметрично расположен внутри трубы длиной M. Между образцом и трубой размещены с малым зазором тороидальные катушки – генераторная и измерительная, расстояние между которыми l (рис. 1). Указанный измерительный зонд расположен в непроводящей среде.
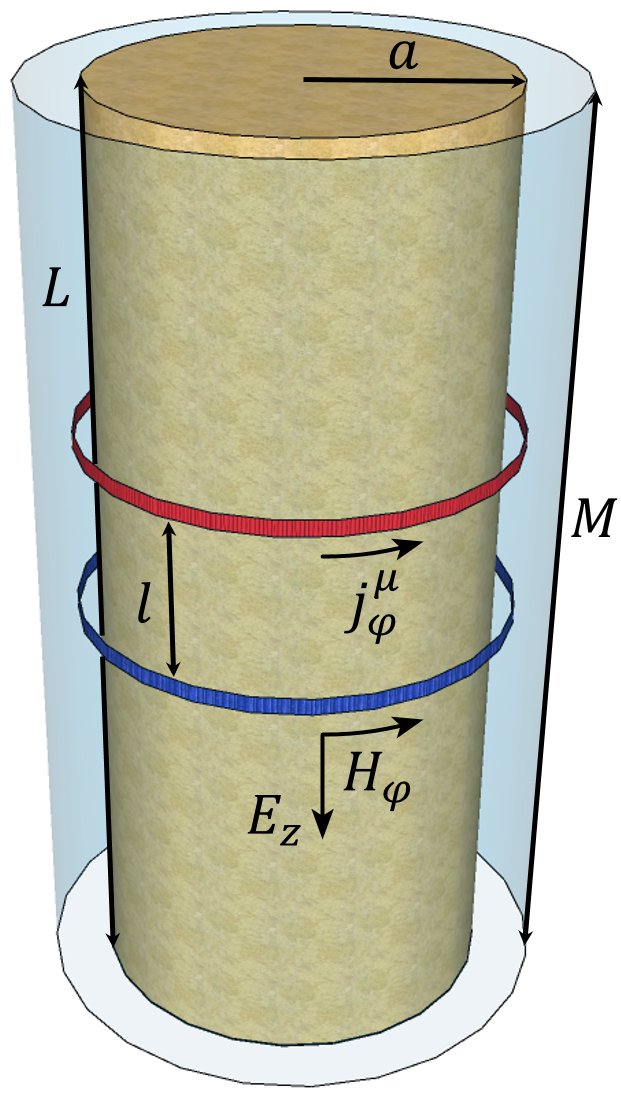
Рис. 1. Геоэлектрическая модель керна (коричневый цвет) и измерительного зонда,
состоящего из генераторной (красный) и измерительной (синий) тороидальных катушек
внутри трубы (голубой)
Введем цилиндрическую систему координат (r, φ, z). Пусть ось z направлена вниз и совпадает с осью цилиндра. Источник поля в виде соосной тороидальной катушки можно описать сторонним круговым магнитным током (Светов, 1984). Для электрического 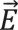 и магнитного
и магнитного 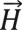 полей в изотропной среде справедливы уравнения Максвелла:
полей в изотропной среде справедливы уравнения Максвелла:
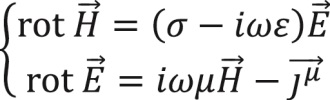 , (1)
, (1)
где 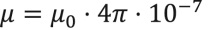 Гн/м – магнитная проницаемость немагнитной среды, ε – диэлектрическая проницаемость среды, ω – циклическая частота,
Гн/м – магнитная проницаемость немагнитной среды, ε – диэлектрическая проницаемость среды, ω – циклическая частота, 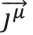 – плотность стороннего магнитного тока.
– плотность стороннего магнитного тока.
В осесимметричной среде плотность стороннего магнитного тока имеет одну ненулевую тангенциальную компоненту:
![]() ,
,
где
![]()
Здесь ![]() – координаты источника, Mφ – магнитный момент, равный:
– координаты источника, Mφ – магнитный момент, равный:
![]() ,
,
где I – ток, nг – число витков в генераторной катушке, Sг – площадь генераторного витка. При расчетах предполагалось, что магнитный момент равен 1 А·м².
С учетом этих факторов систему уравнений (1) можно представить в следующем виде:
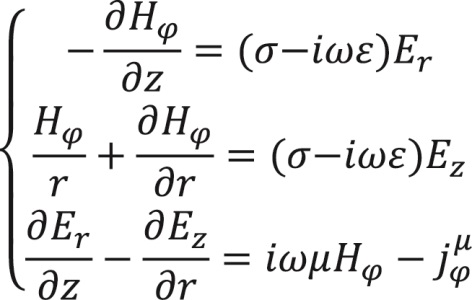 (2)
(2)
Выражая компоненты Er и Ez через Hφ, получаем уравнение
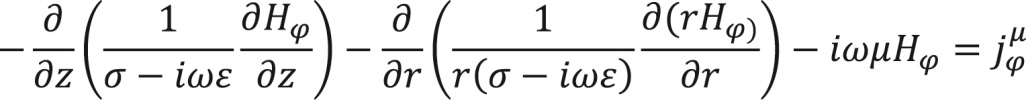 (3)
(3)
Поскольку модель и источник симметричны относительно оси z, имеем
![]()
Затухание магнитного поля вдали от источника запишем в виде
limr,z–›∞|Hφ| –› 0,
следовательно, можно установить нулевые граничные условия для реальной и мнимой составляющих компоненты Hφ на больших расстояниях R и Z от источника:
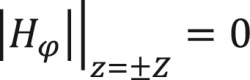
Таким образом, сформулирована краевая задача Дирихле для уравнения (3).
Далее проводим аппроксимацию задачи Дирихле с помощью консервативной конечно-разностной схемы на неравномерной сетке (Самарский, Николаев, 1978). Сетка должна адекватно описывать геоэлектрическую модель, а именно образец, окруженный тонкостенной трубой. При построении сетки требуется учесть большие различия УЭС, возникающие на границе между образцом и трубой. Кроме того, необходимо учесть, что компонента Ez определяется из второго уравнения системы (2), а также необходимо обеспечить достаточную точность для вычисления пространственной производной от Hφ.
В результате аппроксимации получаем систему линейных алгебраических уравнений, которую рекомендуется решать с помощью параллельного варианта программы PARDISO (библиотека Intel Math Kernel Library, https://software.intel.com/en-us/articles/intel-math-kernel-library-documentation), поскольку размерность плохо обусловленной матрицы небольшая. Все вычисления проводились на кластере НКС-30Т ССКЦ СО РАН, однако их можно выполнять и на персональном компьютере.
Для тестирования программы двумерного конечно-разностного моделирования и оптимального выбора сетки использовались опубликованные данные для радиально-слоистых сред, где образец и труба были бесконечно длинными (Эпов и др., 2018). Сравнительный анализ полученных результатов с имеющимися данными показал, что относительная погрешность двумерного моделирования не превышает 1,5% в практически значимом диапазоне УЭС керна.
Влияние конечных размеров керна на результаты моделирования
Рассмотрим однородный керн радиуса 0,040 м с типичным УЭС ρ = 10 Ом·м, соответствующим нефтеводонасыщенному песчанику. Для простоты расчетов примем, что генераторная и измерительная тороидальные катушки имеют радиус 0,040001 м, немного больший радиуса керна, и расположены на стенке непроводящей трубы (УЭС 10⁶ Ом·м) вокруг керна. Внутренний радиус трубы равен 0,040 м, внешний радиус – 0,044 м. Измерительная система окружена воздухом с УЭС 10⁶ Ом·м.
Расстояние между генераторной и измерительной катушкой (длина зонда) l равно 0,10 м. Операционные частоты: 10, 100 и 1 МГц – выбраны из соображений достаточной локальности измерений, а также малого влияния токов смещения.
При расчетах по программе двумерного моделирования длина керна L бралась равной 1,0 м, а при вычислении в цилиндрически-слоистой среде (одномерный подход) она – бесконечная. Для каждой конфигурации расчеты выполнены в одной точке по вертикальной оси, соответствующей середине керна. В табл. 1 приведены реальная и мнимая составляющие: вертикальной компоненты электрического поля (Re Ez, Im Ez) и тангенциальной компоненты магнитного поля (Re Hφ, Im Hφ).
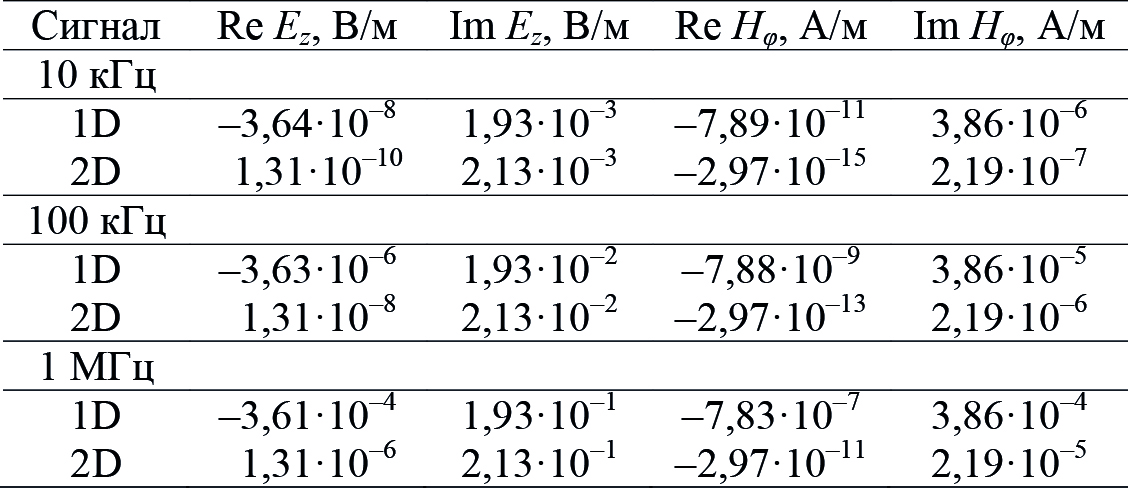
Табл. 1. Результаты одномерного (1D) численно-аналитического
и двумерного (2D) конечно-разностного моделирования.
Короткий зонд, непроводящая труба (УЭС 10⁶ Ом·м),
УЭС однородного образца 10 Ом·м
В результате сопоставительного анализа установлено, что сигналы тороидальной катушки (кругового магнитного тока) при конечной и бесконечной длинах трубы существенно разные. Они могут отличаться как на несколько порядков, так и по знаку (Re Ez), при этом сигналы Re Ez и Re Hφ пропорциональны квадрату операционной частоты, а Im Ez и Im Hφ– частоте. Столь значительное отличие значений физически можно объяснить тем, что в первом случае нет поверхностных зарядов на торцах зонда, препятствующих стеканию токов в окружающую среду. Таким образом, для обоснования параметров измерительной системы на непроводящей трубе следует использовать двумерный подход к моделированию сигналов.
Чувствительность сигналов зонда на непроводящей трубе к УЭС однородного образца
Расчеты выполнены для характерного диапазона УЭС терригенных коллекторов: от 2 до 200 Ом·м. Длина керна равна 1,0 м (координаты по вертикали: от –0,50 до 0,50 м), радиус керна – 0,040 м. Керн окружен непроводящей трубой и воздухом.
Определения УЭС однородного керна велись одновременно перемещаемыми на трубе вдоль керна зондами с l = 0,10; 0,40 и 0,70 м. Результаты моделирования сигналов в средней точке образца приведены в табл. 2.
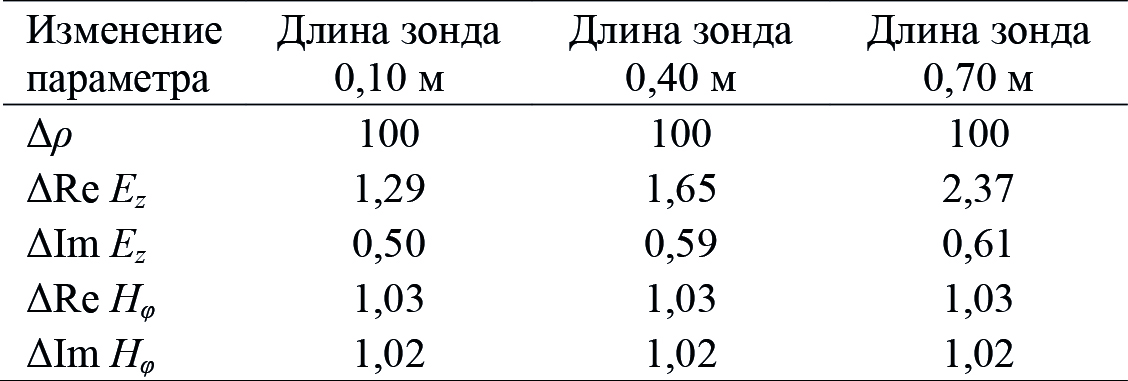
Табл. 2. Относительное изменение сигналов зонда при увеличении УЭС
однородного керна от 2 до 200 Ом·м на частотах от 10 кГц до 1 МГц
При увеличении УЭС керна на два порядка относительное увеличение составляющих Hφ во всех случаях не превышает 1,03. Для Ez при возрастании длины зонда относительное увеличение Re Ez меняется от 1,29 до 2,37, а для Im Ez наблюдается относительное уменьшение – от 0,50 до 0,61.
Наибольшие изменения сигналов, характерные для длинного зонда, показаны на рис. 2 (частота 100 кГц). Здесь и далее составляющие как Hφ, так и Ez представлены по абсолютному значению.
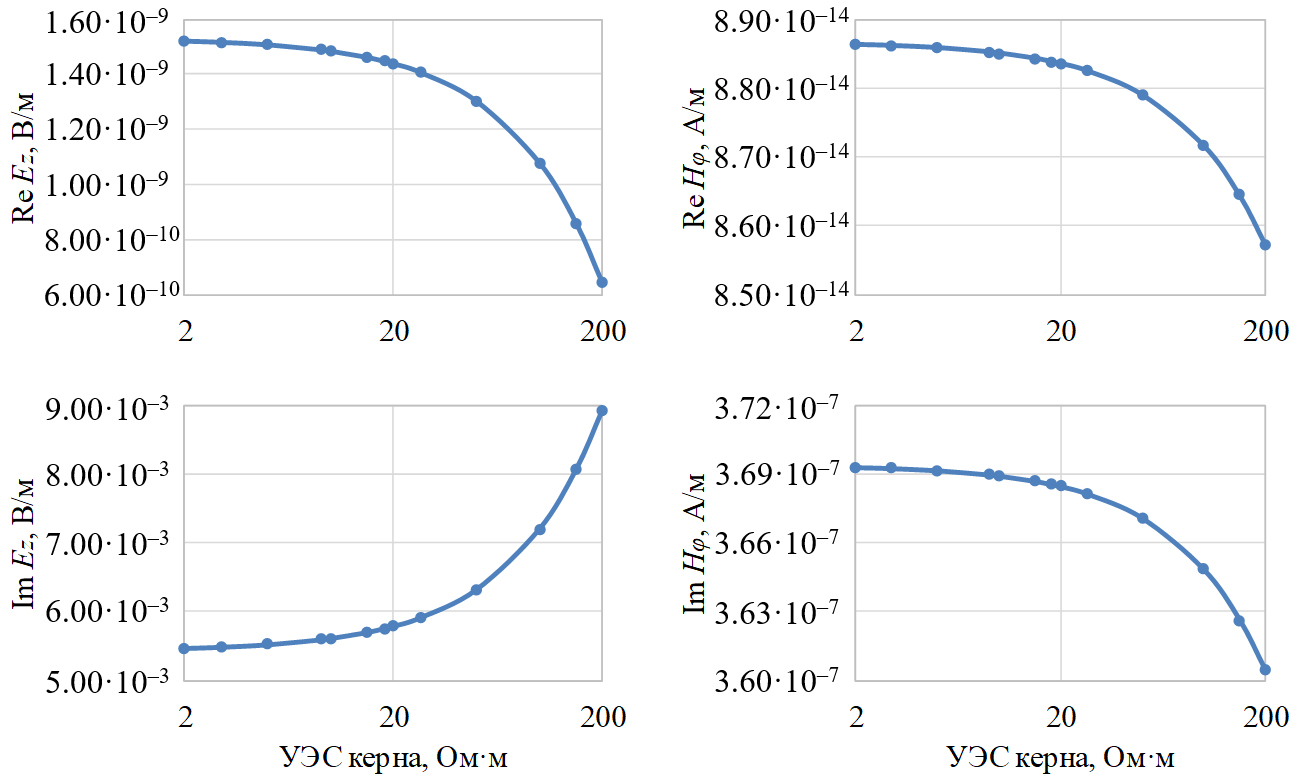
Рис. 2. Зависимость сигналов длинного зонда от УЭС однородного керна.
Частота 100 кГц
Особо выделяется зависимость от УЭС керна для Im Ez: в отличие от остальных составляющих, она увеличивается с ростом УЭС. Это связано с тем, что поле в воздухе для компонент Re Hφ, Im Hφ и Re Ez равно нулю, а для Im Ez – ненулевой константе.
Рассмотрим диаграммы зондов разной длины для Re Hφ (рис. 3, 4). Отметим, что с увеличением длины зонда возрастает локализация диаграмм на интервале образца. Так, истинные границы керна (–0,50 и 0,50 м) выделяются на диаграммах в точках ±0,45 м (зонд 0,10 м), ±0,30 м (зонд 0,40 м) и ±0,15 м (зонд 0,70 м), т.е. кажущаяся граница образца сдвигается внутрь его области на половину длины зонда.
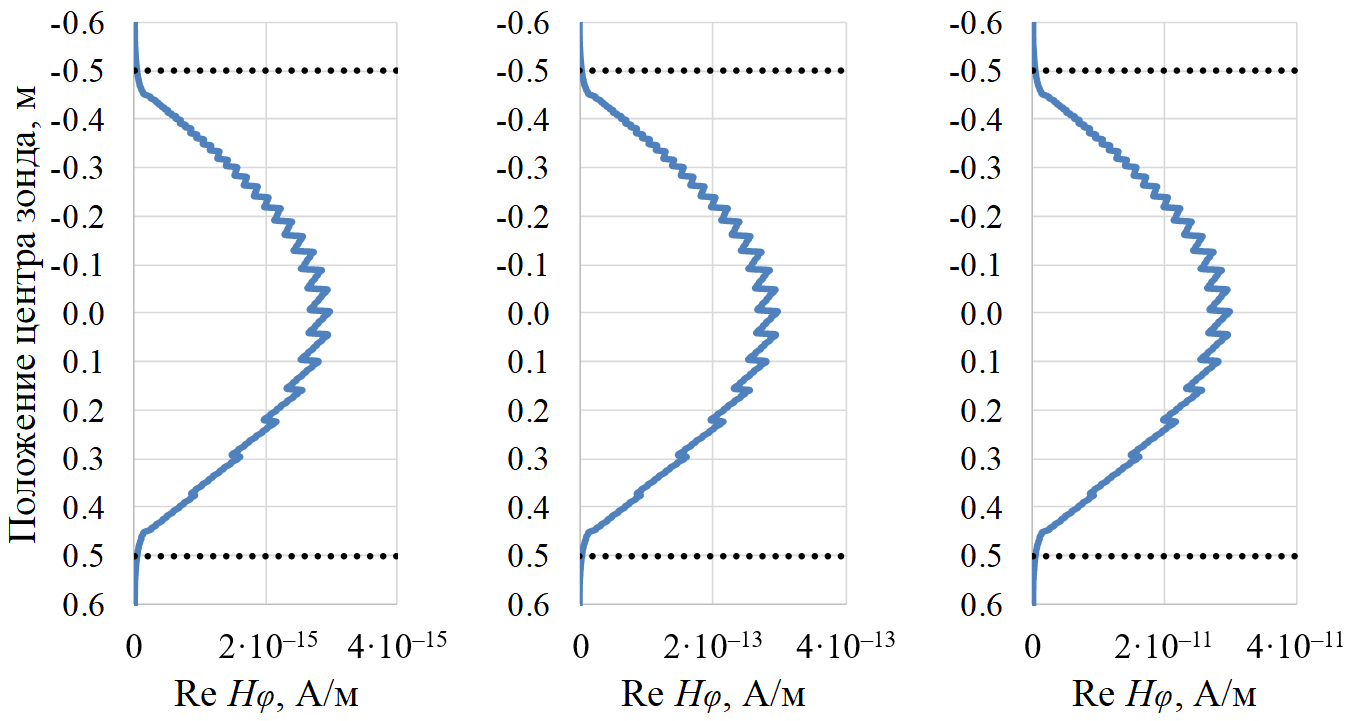
Рис. 3. Диаграммы Re Hφ для короткого зонда
при профилировании однородного керна с УЭС 10 Ом·м.
Слева направо: частота 10 кГц, 100 кГц, 1 МГц.
Пунктирные линии – границы образца
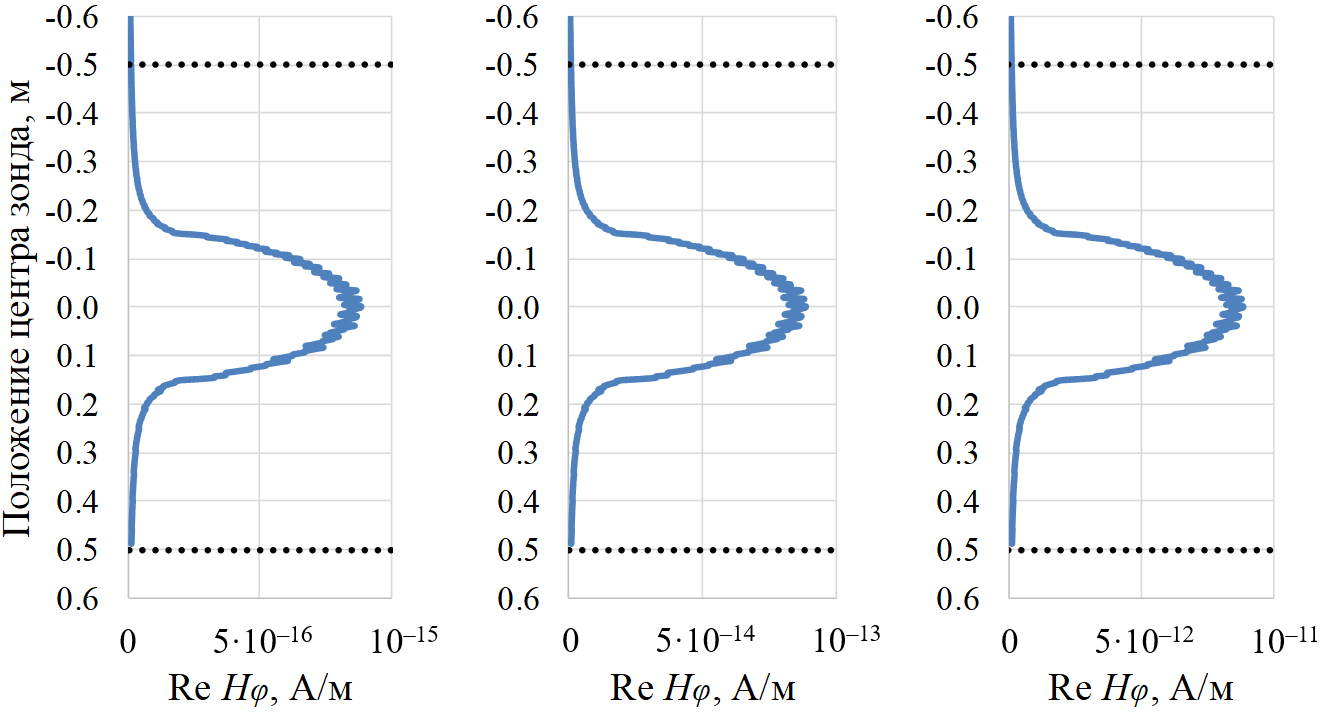
Рис. 4. Диаграммы Re Hφ для длинного зонда
при профилировании однородного керна с УЭС 10 Ом·м.
Слева направо частоты: 10 кГц, 100 кГц, 1 МГц.
Пунктирные линии – границы образца
Даже в коротком зонде (рис. 3) измеренный сигнал Re Hφ в центре образца не достигает истинного значения, а колеблется в области его максимума: 2,97·10–¹⁵ А/м (10 кГц). Для более длинных зондов (рис. 4) выводы аналогичны: с ростом длины зонда сигналы уменьшаются.
На рис. 4 показано сужение кажущейся длины образца, а также увеличение величины Re Hφ с ростом частоты.
Таким образом, сигналы зондов на непроводящей трубе вокруг керна характеризуются очень слабой чувствительностью к изменению его УЭС (от 2 до 200 Ом·м) и малыми уровнями сигналов, что недостаточно для решения практических задач. Однако ситуация становится существенно иной, когда вместо непроводящей трубы образец окружает высокопроводящая металлическая труба.
Чувствительность тороидальных катушек на металлической трубе к УЭС однородного образца
Как и ранее, рассмотрим однородный цилиндрический образец радиуса 0,040 м с УЭС 10 Ом·м. Принципиальное отличие от вышерассмотренного случая состоит в том, что керн окружен высокопроводящей металлической трубой с УЭС 10–⁵ Ом·м. Внутренний и внешний радиусы трубы те же – 0,040 и 0,044 м соответственно. Тороидальные катушки радиуса 0,040001 м расположены на металлической трубе. Вся измерительная система окружена воздухом с УЭС, равным 10⁶ Ом·м. В первом случае (численно-аналитическое решение) керн и металлическая труба имеют бесконечную протяженность, а во втором (конечно-разностное моделирование) длины образца L и металлической трубы M составляют 1,0 м. Численные расчеты показали, что удлинение металлической трубы по обе стороны от керна, например на 0,25 м, слабо влияет на анализируемые сигналы (относительная разница для керна с УЭС 10 Ом·м – сотые доли процента). В табл. 3 представлены результаты моделирования. Для каждого случая расчеты выполнены в одной точке по вертикальной оси, соответствующей середине керна.

Табл. 3. Результаты одномерного численно-аналитического
и двумерного конечно-разностного моделирования сигналов короткого зонда.
Тороидальные катушки на высокопроводящей металлической трубе с УЭС 10–⁵ Ом·м.
УЭС однородного керна 10 Ом·м
Из табл. 3 видно, что результаты одномерных и двумерных расчетов отличаются как по величине (до двух порядков), так и по знаку (компонента Re Hφ). Как и для случая непроводящей трубы, для дальнейших вычислений при определении УЭС керна с помощью тороидальных катушек будет применяться двумерное моделирование сигналов.
Относительные увеличения сигналов при изменении УЭС однородного образца от 2 до 200 Ом·м приведены в табл. 4. При добавлении металлической трубы длиной 1,0 м вокруг керна для короткого зонда происходит резкое увеличение чувствительности к УЭС всех четырех рассматриваемых сигналов. При этом наблюдается прямая пропорциональность УЭС (нижние строки, средний столбец табл. 4). С ростом частоты от 10 кГц до 1 МГц увеличивается чувствительность к УЭС составляющих Re Ez и Re Hφ. Для Im Hφ она практически не меняется, а для Im Ez незначительно уменьшается. На всех рассмотренных частотах с ростом длины зонда чувствительность к УЭС резко падает, а для среднего зонда она отсутствует. Относительное изменение сигналов при увеличении УЭС образца в 100 раз от 2 до 200 Ом·м на частоте 1 МГц близко к результатам на низкой частоте.
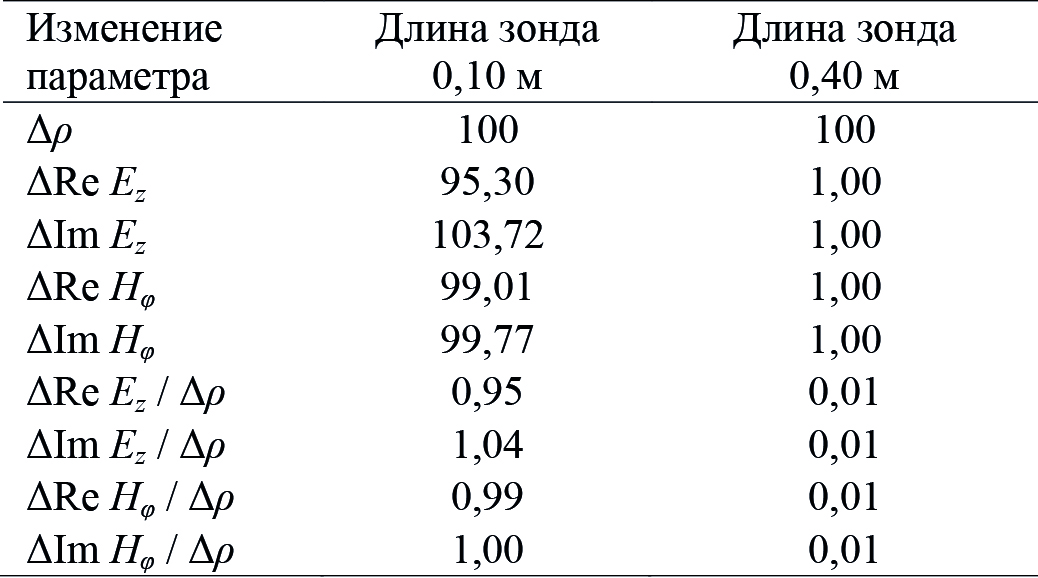
Табл. 4. Относительное изменение сигналов при увеличении УЭС образца в 100 раз
от 2 до 200 Ом·м на частоте 10 кГц. Металлическая труба
Далее приведены примеры профилирования однородного керна с УЭС 10 Ом·м для составляющей Re Hφ. Отметим, что диаграммы для компоненты Im Hφ выглядят аналогично, а для Re Ez и Im Ez характерны дополнительные экстремумы, связанные с переходом тороидальных катушек через границы окруженного металлом керна и усложняющие вид диаграмм. Поэтому в данном случае целесообразно анализировать компоненты Hφ, а не Ez, как более «стабильные». Уровень сигнала Re Hφ пропорционален операционной частоте.
Для короткого зонда (рис. 5) истинные границы керна (–0,50 и 0,50 м) определяются в точках ±0,45 м (сдвинуты к центру образца на половину длины зонда). На всем остальном протяжении керна отмечаются значения сигнала на каждой частоте, соответствующие УЭС керна 10 Ом·м: 3,66·10–⁸, 3,61·10–⁶ и 1,93·10–⁴ А/м.
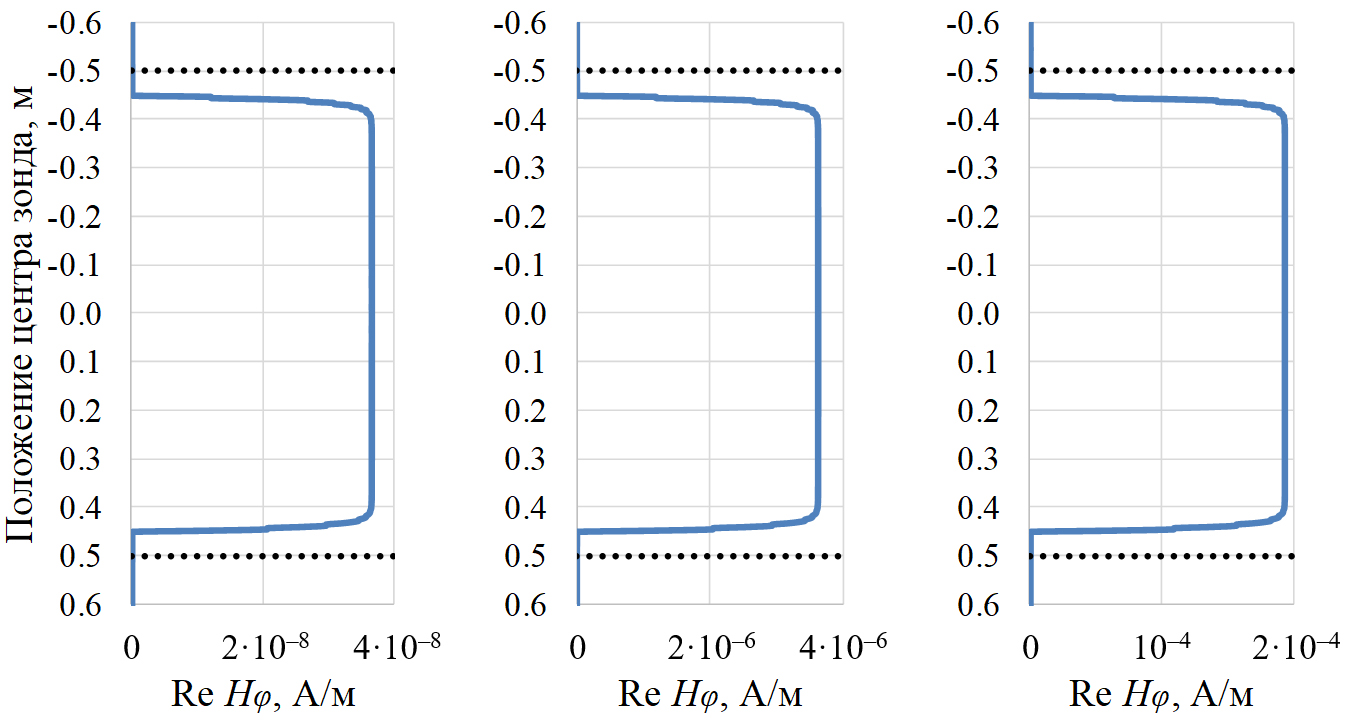
Рис. 5. Кривые Re Hφ при профилировании коротким зондом
однородного образца с УЭС 10 Ом·м.
Слева направо: частоты 10 кГц, 100 кГц, 1 МГц.
Пунктирные линии – границы керна
Для длинного зонда (рис. 6), как и для среднего, не достигается истинное значение сигнала. Внутри образца на половине длины зонда (0,35 м) также появляются аналогичные экстремумы. Значения сигналов на разных частотах в центре керна равны 5,76·10–¹², 5,48·10–¹⁰ и 8,41·10–¹⁰ А/м соответственно.
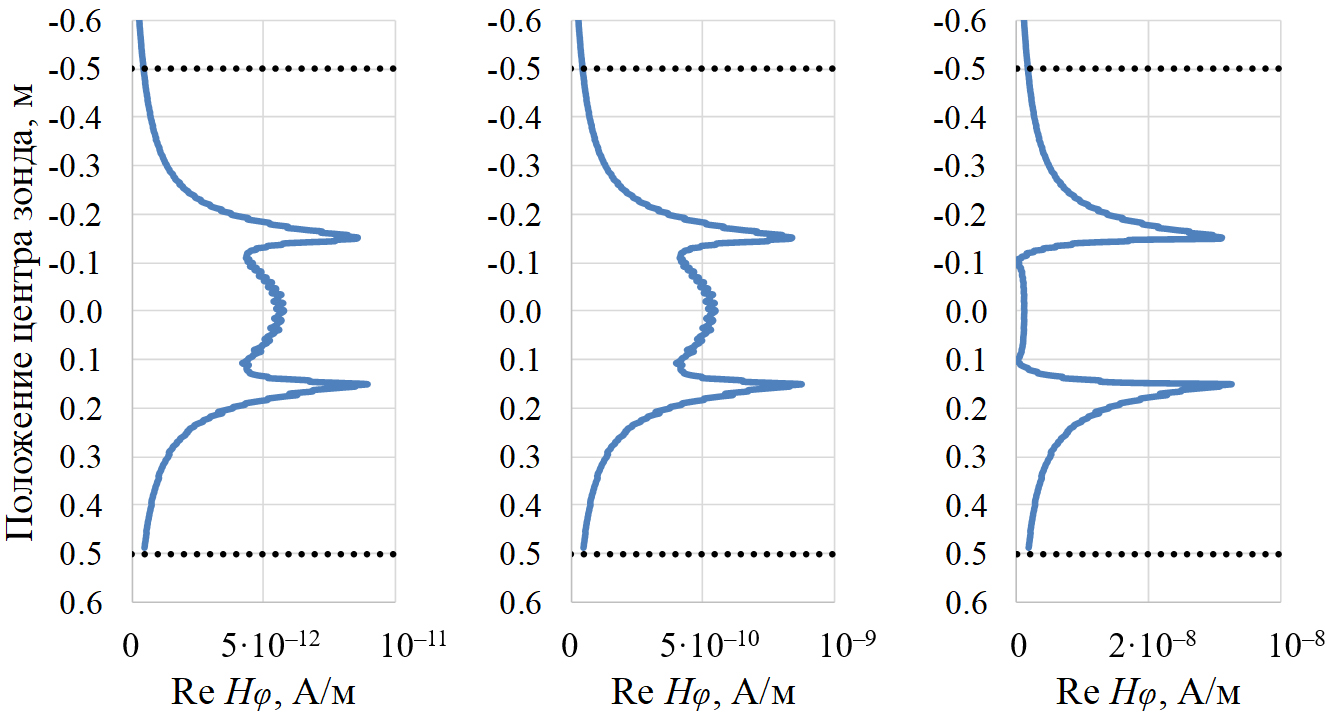
Рис. 6. Кривые Re Hφ при профилировании длинным зондом
однородного образца с УЭС 10 Ом·м.
Слева направо: частоты 10 кГц, 100 кГц, 1 МГц.
Пунктирные линии – границы керна
Из анализа приведенных на рис. 5, 6 диаграмм следует: во-первых, для определения УЭС керна наиболее оптимально использовать короткий зонд; во-вторых, уровень сигналов при наличии металлической трубы вокруг керна на несколько порядков выше, чем при ее отсутствии.
Далее нами для короткого зонда построены зависимости сигналов от УЭС однородного цилиндрического образца. На их основе получены графики трансформаций сигналов в кажущиеся УЭС керна: для Re Hφ (рис. 7) и Im Hφ (рис. 8), а также для Re Ez и Im Ez (в настоящей статье не приведены).
Отметим, что все трансформации являются взаимно однозначными.
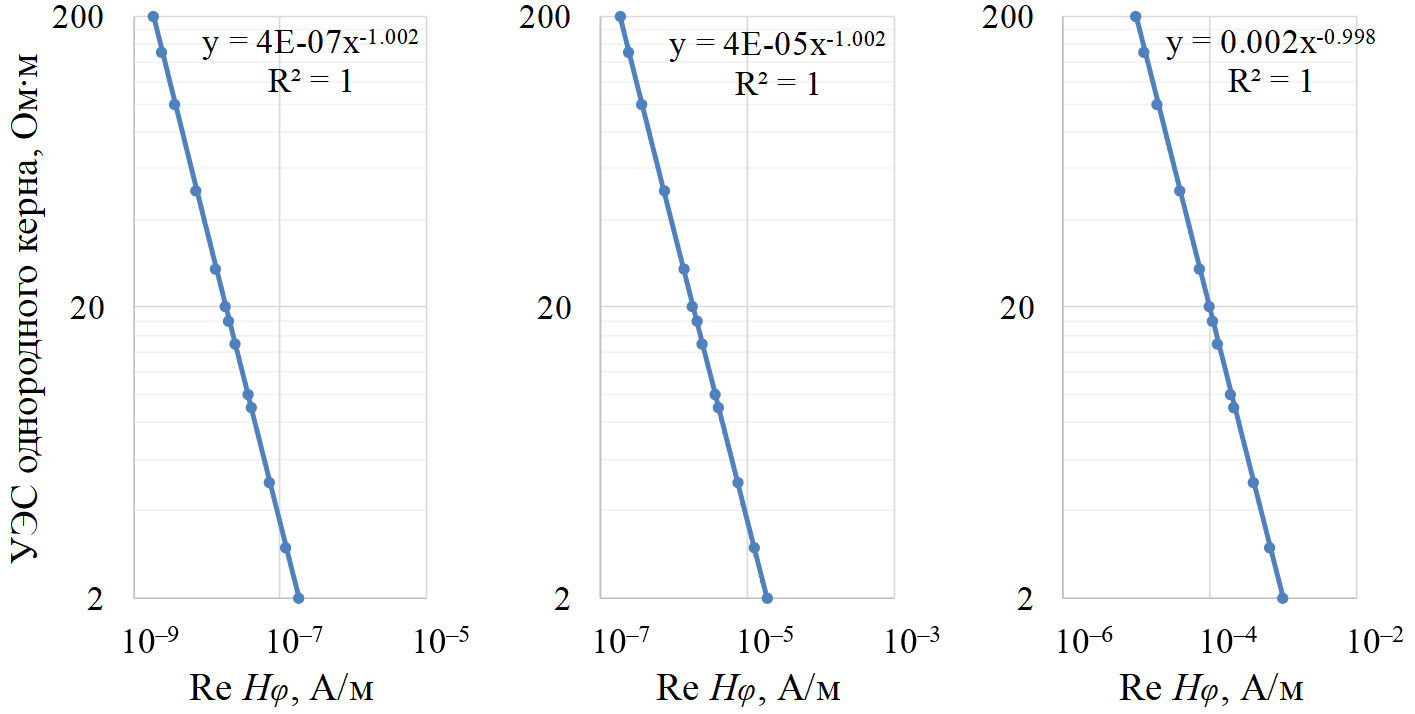
Рис. 7. Графики трансформаций Re Hφ короткого зонда в УЭС образца
для тороидальных катушек на металлической трубе.
Частоты: 10 кГц (слева), 100 кГц (по центру), 1 МГц (справа)
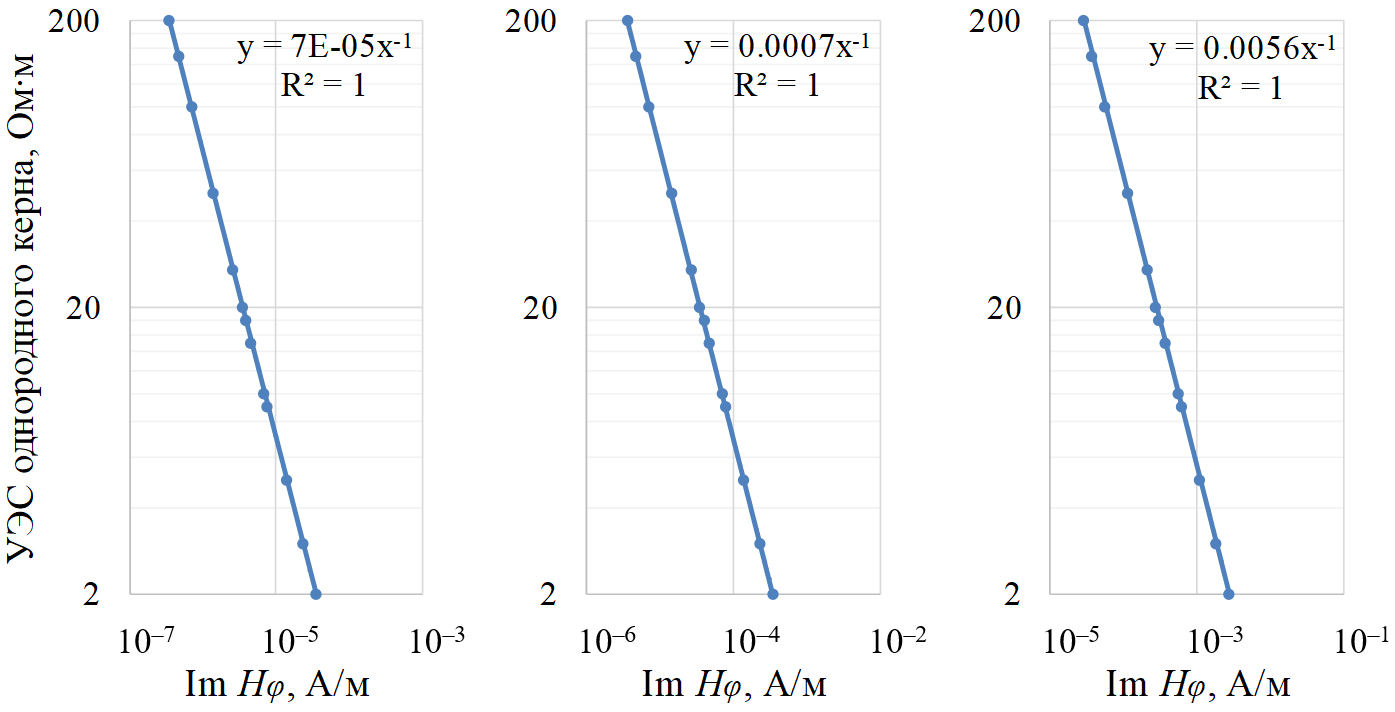
Рис. 8. Графики трансформаций Im Hφ короткого зонда в УЭС керна
для тороидальных катушек на металлической трубе.
Частоты: 10 кГц (слева), 100 кГц (по центру), 1 МГц (справа)
Трансформации сигналов тороидальной катушки в кажущиеся УЭС составного керна
Рассмотрим составной вертикально-неоднородный цилиндрический образец той же длины 1,0 м и радиуса 0,040 м. Керн состоит из четырех частей равной длины 0,25 м с монотонно увеличивающимся УЭС (в четыре раза) от его верхней части к нижней: 2–8–32–128 Ом·м. Для заданного распределения УЭС керна рассчитаны все анализируемые сигналы. Далее проведен пересчет измеренных сигналов Re Hφ и Im Hφ (рис. 9) и Re Ez и Im Ez (рис. 10) в значения кажущегося УЭС.
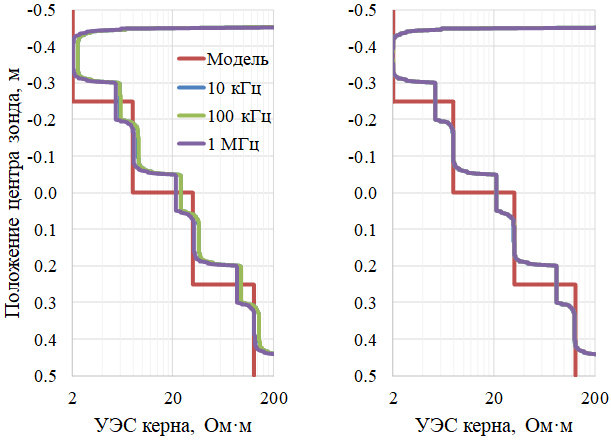
Рис. 9. Кажущиеся УЭС по Re Hφ (слева) и Im Hφ (справа) короткого зонда
в составном образце с монотонным увеличением УЭС. Металлическая труба
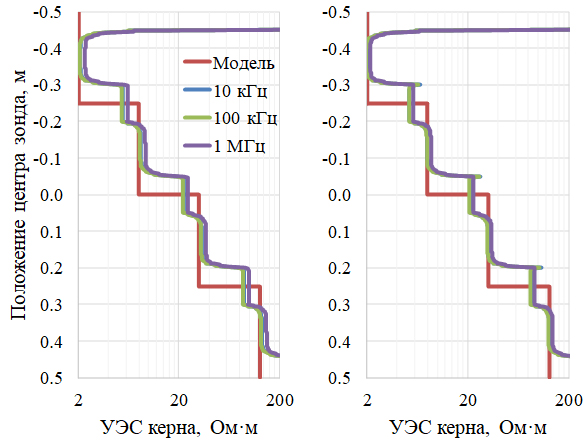
Рис. 10. Кажущиеся УЭС по Re Ez (слева) и Im Ez (справа) короткого зонда
в составном образце с монотонным увеличением УЭС. Металлическая труба
Относительно погрешности определения УЭС составного керна стоит отметить, что с минимальными относительными погрешностями определяется УЭС в центральной части каждой из четырех частей. В краевых частях кажущиеся УЭС арифметически усредняются с УЭС смежных частей. Кажущиеся УЭС по Re Hφ (рис. 9, слева) везде завышены относительно истинных. Так, на частотах 10 и 100 кГц для всех четырех частей образца относительное завышение составляет 12,4–13,6%, а на частоте 1 МГц – лишь 1,2–1,6%. Кажущиеся УЭС по Im Hφ (рис. 9, справа) занижены относительно истинных на 0,7–1,1%, (частота 10 кГц) и 0,2–0,6% (частоты 100 кГц и 1 МГц).
Для кажущихся УЭС по Re Ez и Im Ez (рис. 10) картина будет иной. По Re Ez отмечается завышение УЭС, причем наибольшее при 1 МГц (14–17%). На частоте 10 кГц завышение составляет 4,1–5,6%, а на 100 кГц оно наименьшее – 2,2–3,5%. Для Im Ez ситуация будет менее однозначной. Наибольшее завышение УЭС (на 8,1%) также имеется при 1 МГц. При 100 кГц УЭС занижается на 0,4–1,6%. Наконец, при 10 кГц кажущееся УЭС как завышается на 0,1–1,1%, так и занижается на 0,3%. Добавим, что на трансформациях по Im Ez присутствуют небольшие ложные экстремумы на отметках –0,03; –0,05 и 0,20 м (рис. 10, справа).
При изменении УЭС частей (2–32–8–128 Ом·м) в составном образце с повышением контраста между смежными частями (рис. 11) в целом наблюдаются все те же закономерности.
Итак, с учетом отмеченных особенностей наиболее оптимальной является трансформация в кажущееся УЭС по сигналу Im Hφ на частоте 1 МГц.
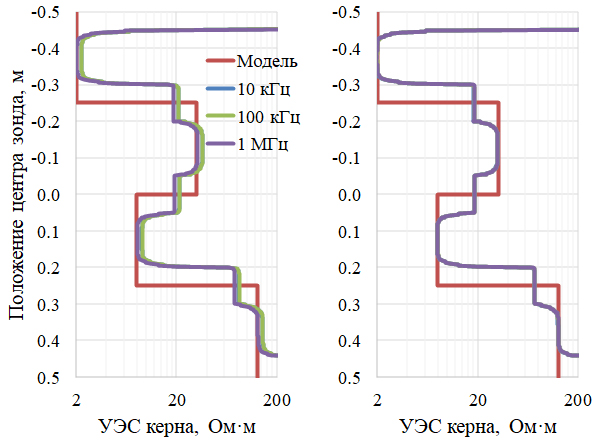
Рис. 11. Кажущиеся УЭС по Re Hφ (слева) и Im Hφ (справа) короткого зонда
в составном образце с немонотонным увеличением УЭС. Металлическая труба
Сигналы тороидальных катушек на металлической трубе вокруг тонкослоистого образца
Далее проведено двумерное моделирование сигналов тороидальных катушек на металлической трубе, окружающих тонкослоистые цилиндрические образцы длиной 1,0 м. Толщина прослоев в каждом исследуемом керне одинакова и составляет 0,10; 0,05; 0,04; 0,03; 0,02 и 0,01 м. Рассмотрены два случая соотношения УЭС соседних прослоев: 3–9 Ом·м (контраст 3, соответствует чередованию глин и нефтеводонасыщенных песчаников), а также 3–27 Ом·м (контраст 9, чередование глин и нефтенасыщенных песчаников). Для установления взаимосвязи показаний измерительной системы с тороидальными катушками в тонкослоистой и электрически макроанизотропной средах выполнены расчеты составляющих Ez и Hφ. Макроанизотропная среда для УЭС 3–9 Ом·м имеет следующие параметры: горизонтальное УЭС ρh = 4,5 Ом·м, вертикальное УЭС ρv = 6 Ом·м; макроанизотропная среда для УЭС 3–27 Ом·м – ρh = 5,4 Ом·м, ρv = 15 Ом·м. На рис. 12 и 13 представлены численные результаты для компоненты Im Hφ на частоте 1 МГц для короткого зонда, которые в целом отражают особенности и остальных компонент, включая другие операционные частоты.
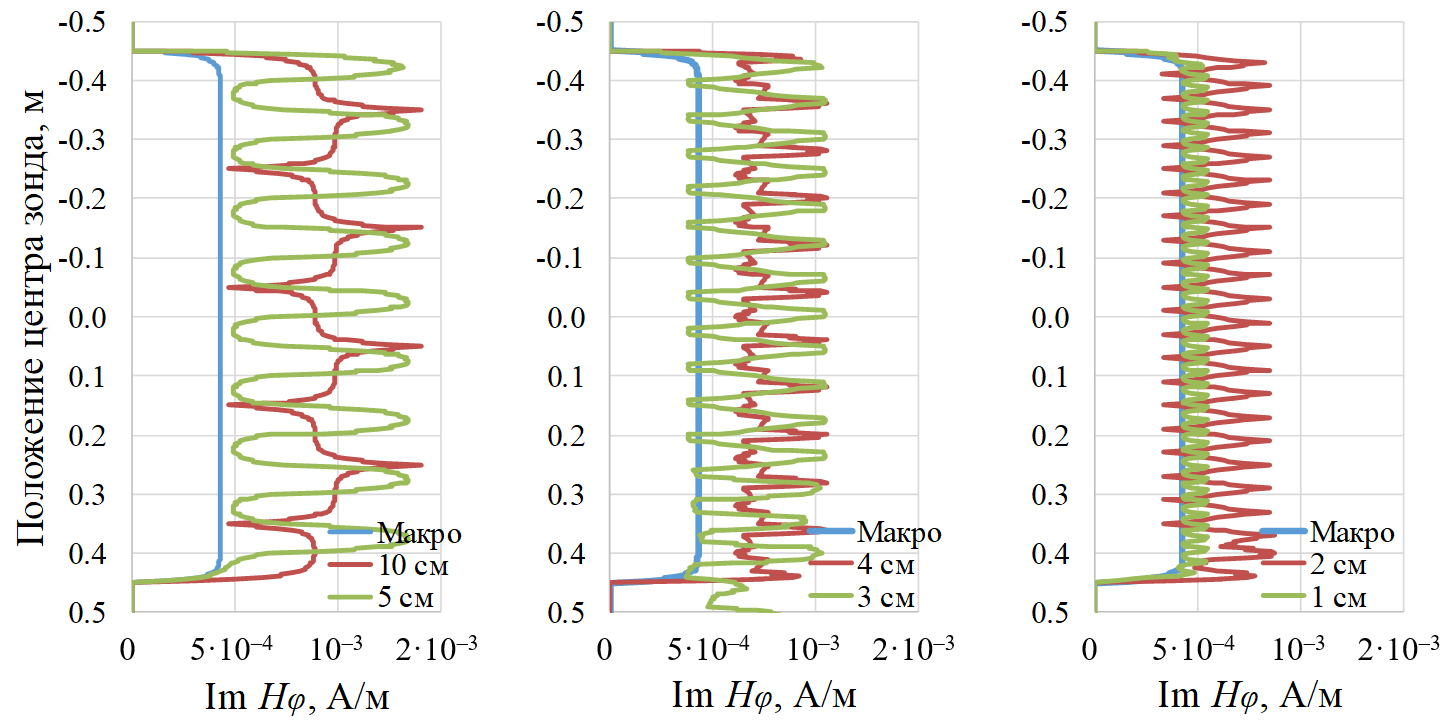
Рис. 12. Диаграммы Im Hφ короткого зонда
в тонкослоистом и эквивалентном макроанизотропном образцах.
УЭС смежных прослоев 3–9 Ом·м. Частота 1 МГц
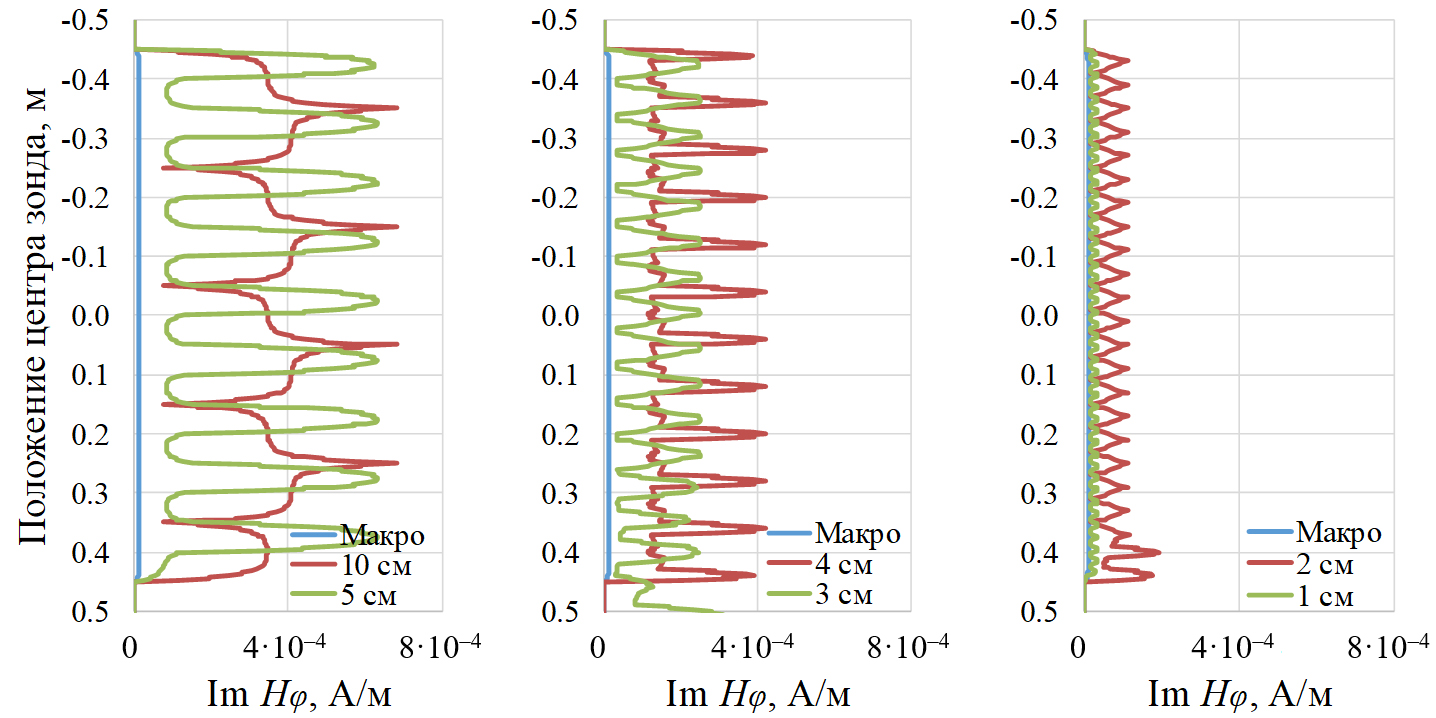
Рис. 13. Диаграммы Im Hφ короткого зонда
в тонкослоистом и эквивалентном макроанизотропном образцах.
УЭС смежных прослоев 3–27 Ом·м. Частота 1 МГц
Диапазон изменений Im Hφ при электрическом контрасте 3 (рис. 12) составляет от 4,72·10–⁴ до 1,41·10–³ А/м при прослоях толщиной 0,10 м и от 4,29·10–⁴ до 5,46·10–⁴ А/м при прослоях толщиной 0,01 м. При увеличении контраста до 9 (рис. 13) Im Hφ варьируется в пределах 7,70·10–⁵–6,81·10–⁴ А/м (прослои толщиной 0,10 м) и 1,85·10–⁵–3,39·10–⁵ А/м (прослои толщиной 0,01 м).
Из анализа диаграмм для тонкослоистых образцов на рис. 12 и 13 следует: во-первых, за счет компактности измерительной системы и выбранного диапазона частот выделяются все отдельные прослои в диапазоне их толщин от 0,10 до 0,01 м; во-вторых, при электрическом контрасте 9 (3–27 Ом·м, рис. 13) диаграммы в тонкослоистых кернах и эквивалентной им макроанизотропной среде не имеют общих точек, хотя стремятся друг к другу с уменьшением толщины прослоев. Иными словами, даже при прослоях в 0,01 м керн воспринимается системой с тороидальными катушками как тонкослоистый, а не как макроанизотропный.
Отдельно остановимся на рис. 12. При толщине прослоев 0,03 м соответствующая диаграмма в тонкослоистом образце накладывается на диаграмму в макроанизотропном образце. Еще в большей степени это проявляется при прослоях толщиной 0,02 м. Наконец, при толщине прослоев 0,01 м соответствующая «макроанизотропная» диаграмма становится огибающей для «тонкослоистой» диаграммы, что может указывать на достигаемую эквивалентность между тонкослоистостью и макроанизотропией при отношении длины зонда к толщине прослоя большем 10.
Для проверки этой эквивалентности для диаграммы с прослоями толщиной 0,01 м и соотношением УЭС 3–9 Ом·м вычислено ее относительное отклонение от среднего. Оно составляет 12%, т.е. полная эквивалентность еще не достигнута. Для соотношения УЭС 3–27 Ом·м относительное отклонение значительно больше – около 29%. При этом тонкослоистый керн будет восприниматься измерительной системой как макроанизотропный, когда такое отклонение будет сопоставимо с относительной погрешностью двумерного моделирования, не превышающей 1,5%. Таким образом, можно ожидать такой эквивалентности, когда толщина каждого прослоя будет составлять несколько миллиметров.
Заключение
Предложен компактный зонд с тороидальными катушками для определения УЭС кернового материала. При математическом описании тороидальной катушки сторонним круговым магнитным током, разработаны специализированные программно-алгоритмические средства двумерного конечно-разностного моделирования, учитывающие как конечные размеры керна с заданным УЭС, так и высокий электрический контраст в геоэлектрической модели. Проведена верификация компьютерной программы на основе сравнения с численно-аналитическим решением в рамках одномерных цилиндрически-слоистых моделей.
Рассмотрено два основных случая, когда генераторная и измерительная тороидальные катушки расположены соответственно на изолирующей и сильнопроводящей металлической трубе вокруг керна. Показано, что в случае металлической трубы для короткого зонда достигается высокая чувствительность всех возбуждаемых сигналов к характерным значениям УЭС керна. Для однородных кернов построены взаимно однозначные трансформации сигналов в кажущееся УЭС. С использованием трансформаций получены достоверные распределения УЭС составных вертикально-неоднородных образцов. Проведено двумерное численное моделирование сигналов в тонкослоистых кернах, где толщина прослоя составляет от 0,01 до 0,10 м, и в эквивалентных им электрически макроанизотропных средах при разных контрастах УЭС. Сделан вывод о том, что даже при прослоях в 0,01 м керн проявляется в сигналах тороидальной системы как тонкослоистый; эквивалентности тонкослоистого и электрически-макроанизотропного керна следует ожидать при меньшей толщине прослоев.
Таким образом, можно заключить, что имеется принципиальная возможность определения УЭС кернового материала при размещении вокруг него измерительной системы с тороидальными катушками на сильнопроводящей трубе как во время бурения, так и при лабораторных измерениях.
Финансирование
Исследование выполнено при финансовой поддержке проекта ФНИ № FWZZ-2022-0026 «Инновационные аспекты электродинамики в задачах разведочной и промысловой геофизики».
Список литературы
1. Герке К.М., Корост Д.В., Карсанина М.В., Корост С.Р., Васильев Р.В., Лаврухин Е.В., Гафурова Д.Р. (2021). Изучение и анализ современных подходов к построению цифровых моделей керна и методов моделирования многофазной фильтрации в масштабах порового пространства. Георесурсы, 23(2), c. 197–213. https://doi.org/10.18599/grs.2021.2.20
2. Каринский А.Д. (2018). Электромагнитное поле в моделях электрически анизотропной среды. М.: ГЕОС , 184 с.
3. Мезин А.А., Шумскайте М.Й., Глинских В.Н., Голиков Н.А., Чернова Е.С. (2020). Фильтрационно-емкостные свойства бурового шлама по данным ядерно-магнитной резонансной релаксометрии и диэлектрической спектроскопии. Науки о Земле и недропользование, 43(3), с. 364–374. https://doi.org/10.21285/2686-9993-2020-43-3-364-374
4. Решетова Г.В., Анчугов А.В. (2021). Цифровой керн: моделирование акустической эмиссии в целях локализации ее источников методом обращения волнового поля в обратном времени. Геология и геофизика, 62(4), с. 597–609. https://doi.org/10.15372/GiG2020148
5. Самарский А.А., Николаев Е.С. (1978). Методы решения сеточных уравнений. М.: Наука, 592 с.
6. Светов Б.С. (1984). Электродинамические основы квазистационарной геоэлектрики. М.: ИЗМИРАН, 183 с.
7. Фадеева И.И., Дучков А.А., Манаков А.Ю., Аюнов Д.Е. (2020). Количественная оценка содержания гидрата СО 2 в лабораторных образцах с помощью двухигольчатого зонда. Геофизические исследования, 21(2), с. 61–77. https://doi.org/10.21455/gr2020.2-5
8. Хачкова Т.С., Лисица В.В., Решетова Г.В., Чеверда В.А. (2020). Численная оценка удельного электрического сопротивления горных пород по их цифровым изображениям с использованием графических сопроцессоров. Вычислительные методы и программирование, 21(3), с. 306–318. https://doi.org/10.26089/NumMet.v21r326
9. Хачкова Т.С., Лисица В.В., Сотников О.С., Исламов И.А., Ганиев Д.И. (2023). Новая методика численной оценки абсолютной проницаемости горных пород по их микротомографическим изображениям. Геофизика, (1), с. 34–40. https://doi.org/10.34926/geo.2023.46.58.005
10. Шумскайте М.Й., Ян П.А., Голиков Н.А. (2022). Релаксационные характеристики образцов керна на примере параметрической скважины: база данных фильтрационно-емкостных свойств по ЯМР-данным. Геофизические технологии, (1), с. 88–98. https://doi.org/10.18303/2619-1563-2022-1-88
11. Эпов М.И., Никитенко М.Н., Глинских В.Н. (2018). Математическое обоснование нового электромагнитного зонда с тороидальными катушками для высокоразрешающего каротажа нефтегазовых скважин. Вестник НГУ. Серия: Информационные технологии, 16(1), с. 113–129. https://doi.org/10.25205/1818-7900-2018-16-1-113-129
12. Эпов М.И., Шурина Э.П., Добролюбова Д.В., Кутищева А.Ю., Марков С.И., Штабель Н.В., Штанько Е.И. (2023). Определение эффективной электропроводности флюидонасыщенного керна по данным компьютерной томографии. Физика Земли, (5), с. 13–23. https://doi.org/10.31857/S0002333723050046
13. Ahmed H.M., Ahmed H.A.M., Adewuyi S.O. (2021). Characterization of Microschist Rocks under High Temperature at Najran Area of Saudi Arabia. Energies, 14(22), 7612. https://doi.org/10.3390/en14227612
14. Ashrafi J., Faramarzi L., Darbor M., Sharifzadeh M., Ferdosi B. (2020). The effects of temperature on mechanical properties of rocks. International Journal of Mining and Geo-Engineering, 54(2), pp. 147–152. https://doi.org/10.22059/ijmge.2019.271982.594771
15. Ben Aoun N., Kouki A., Aouina N., Haj Amara A.B. (2018). Radial Electrical Resistivity Measurements of Rocks on Laboratory Core Samples Using an Electromagnetic Sensor: Macro and Micro Eddy Currents. Journal of Sensors, 2018, 6435070. https://doi.org/10.1155/2018/6435070
16. Elsayed M., Isah A., Hiba M., Hassan A., Al-Garadi K., Mahmoud M., El‑Husseiny A., Radwan A.E. (2022). A review on the applications of nuclear magnetic resonance (NMR) in the oil and gas industry: laboratory and field‑scale measurements. Journal of Petroleum Exploration and Production Technology, 12, pp. 2747–2784. https://doi.org/10.1007/s13202-022-01476-3
17. Gu B., Wan Z., Zhang Y., Ma Y., Xu X.B. (2020). Influence of Real-Time Heating on Mechanical Behaviours of Rocks. Advances in Civil Engineering, 2020, 8879922. https://doi.org/10.1155/2020/8879922
18. Kästner F., Klaeschen D., Berndt C., Pierdominici S., Hedin P. (2022). Anisotropic velocity models for (3-D) seismic imaging of the Lower Seve Nappe in Jämtland, Sweden. Geophysical Journal International, 228(1), pp. 66–77. https://doi.org/10.1093/gji/ggab339
19. Kästner F., Pierdominici S., Elger J., Zappone A., Kück J., Berndt C. (2020). Correlation of core and downhole seismic velocities in high-pressure metamorphic rocks: A case study for the COSC-1 borehole, Sweden. Solid Earth, 11(2), pp. 607–626. https://doi.org/10.5194/se-11-607-2020
20. Kim J.-W., Hong C.-H., Kim J.-S., Chong S.-H. (2021). Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes. Energies, 14(14), 4382. https:// doi.org/10.3390/en14144382
21. Li J., Ke S., Yin C., Kang Z., Jia J., Ma X. (2019). A laboratory study of complex resistivity spectra for predictions of reservoir properties in clear sands and shaly sands. Journal of Petroleum Science and Engineering, 177, pp. 983–994. https://doi.org/10.1016/j.petrol.2019.01.061
22. Liu H.Q., Tian J., Youming D., Chunning Q. (2016). Study of the lowfrequency dispersion of permittivity and resistivity in tight rocks. International Journal of Petrochemical Science & Engineering, 1(3), pp. 55‒61. https:// doi.org/10.15406/ipcse.2016.01.00011
23. Luc Leroy M.N., Marius F.W., François N. (2021). Experimental and Theoretical Investigations of Hard Rocks at High Temperature: Applications in Civil Engineering. Advances in Civil Engineering, 2021, 8893944. https:// doi.org/10.1155/2021/8893944
24. Morte M., Hascakir B. (2019). Characterization of complex permittivity for consolidated core samples by utilization of mixing rules. Journal of Petroleum Science and Engineering, 181, 106178. https://doi.org/10.1016/j.petrol.2019.06.042
25. Ponomarev A.A., Kadyrov М.А., Tugushev O.A., Drugov D.A., Vaganov Y.V., Leontiev D.S., Zavatsky M.D. (2024). Digital core reconstruction research: challenges and prospects. Geology, Ecology, and Landscapes, 8(1), pp. 49–56. https://doi.org/10.1080/24749508.2022.2086201
26. Sharifi J., Nooraiepour M., Amiri M., Mondol N.H. (2023). Developing a relationship between static Young’s modulus and seismic parameters. Journal of Petroleum Exploration and Production Technology, 13, pp. 203–218. https://doi.org/10.1007/s13202-022-01546-6
27. Shumskayte M., Mezin A., Chernova E., Burukhina A., Golikov N., Melkozerova S. (2022). Estimating Water Content in Water–Oil Mixtures and Porous MEDIA They Saturate: Joint Interpretation of NMR Relaxometry and Dielectric Spectroscopy. Geosciences, 12(4), 179. https://doi.org/10.3390/geosciences12040179
Об авторах
М. И. ЭповРоссия
Михаил Иванович Эпов – доктор тех. наук, профессор, академик РАН, главный научный сотрудник
630090, Новосибирск, пр. Ак. Коптюга, д. 3
В. Г. Мамяшев
Россия
Венер Галиуллинович Мамяшев – кандидат геол.-мин. наук, доцент кафедры прикладной геофизики
625000, Тюмень, ул. Володарского, д. 38
И. В. Михайлов
Россия
Игорь Владиславович Михайлов – кандидат тех. наук, старший научный сотрудник; доцент
630090, Новосибирск, пр. Ак. Коптюга, д. 3
630090, Новосибирск, ул. Пирогова, д. 1
И. В. Суродина
Россия
Ирина Владимировна Суродина – кандидат физ.-мат. наук, старший научный сотрудник
630090, Новосибирск, пр. Ак. Коптюга, д. 3
М. Н. Никитенко
Россия
Марина Николаевна Никитенко – доктор тех. наук, ведущий научный сотрудник
630090, Новосибирск, пр. Ак. Коптюга, д. 3
Рецензия
Для цитирования:
Эпов М.И., Мамяшев В.Г., Михайлов И.В., Суродина И.В., Никитенко М.Н. Определение удельного электрического сопротивления керна с помощью тороидальных катушек: математическое моделирование. Георесурсы. 2024;26(3):151-161. https://doi.org/10.18599/grs.2024.3.16
For citation:
Epov M.I., Mamyashev V.G., Mikhaylov I.V., Surodina I.V., Nikitenko M.N. Application of Toroidal Coils to Obtain Electrical Resistivity of Core Samples: Mathematical Modeling. Georesursy = Georesources. 2024;26(3):151-161. (In Russ.) https://doi.org/10.18599/grs.2024.3.16















.png)


