Перейти к:
Модель взаимодействия скважин при заводнении слоисто-неоднородного нефтяного пласта в рамках концепции CRM-моделирования
https://doi.org/10.18599/grs.2024.3.17
Аннотация
Рассмотрены основные виды CRM-моделей (Capacitance Resistive Model). Преимуществом CRM-моделей перед другими типами моделей является исключение из рассмотрения пластового давления, информация о котором обычно носит несистемный, разрозненный, а часто и недостоверный характер. Особое внимание в работе уделено многослойным CRM-моделям, описывающим поток в слоистых пластах. По литературным данным описаны три модели, наиболее близкие к предлагаемой в данной работе.
Предложена авторская модель взаимодействия скважин при заводнении нефтяного пласта с двойной проницаемостью (частный случай слоисто-неоднородного пласта) в рамках концепции CRM-моделирования. Отличия предлагаемой модели от моделей других авторов состоят в следующем: 1) модель учитывает возможные перетоки между слоями за счет вертикальной фильтрации поперек напластования; 2) модель учитывает двухфазный характер фильтрации при заводнении, благодаря использованию дифференциального уравнения сохранения объема воды в пластовых условиях, такой подход является наиболее точным и физически обоснованным; 3) дифференциальные уравнения модели решаются с помощью численных методов; 4) рассматривается система, состоящая из двух слоев с разными фильтрационно-емкостными свойствами.
Проведено тестирование предложенного подхода на модельных и фактических данных. В модельном примере при сравнении различных показателей разработки, рассчитанных с помощью CRM-модели и с помощью гидродинамического симулятора, коэффициент детерминации составляет не менее 0.9. Это является хорошим результатом и говорит о высоком уровне совпадения кривых. В фактическом примере при сравнении рассчитанных с помощью CRM-модели и фактических показателей разработки коэффициент детерминации составляет не менее 0.7. Это, как и в предыдущем случае, является хорошим результатом для фактических данных и говорит о высоком уровне совпадения расчетных и фактических кривых.
Для цитирования:
Глушаков А.А., Архипов А.И., Афанаскин И.В. Модель взаимодействия скважин при заводнении слоисто-неоднородного нефтяного пласта в рамках концепции CRM-моделирования. Георесурсы. 2024;26(3):162-174. https://doi.org/10.18599/grs.2024.3.17
For citation:
Glushakov A.A., Arhipov A.I., Aafanaskin I.V. Model of Well Interference During Waterflooding of a Layered Heterogeneous Oil Reservoir within the Framework of the CRM Modeling Concept. Georesursy = Georesources. 2024;26(3):162-174. (In Russ.) https://doi.org/10.18599/grs.2024.3.17
Введение
CRM-модель (Capacitance Resistive Model) или емкостно-резистивная модель – это математическая модель, описывающая интерференцию скважин в пласте с использованием уравнений двух видов: уравнения сохранения объема жидкости (обычно в пластовых условиях), отвечающего за «емкость» (C), и уравнения притока к скважине, отвечающего за сопротивление (R). Емкостное уравнение является видом уравнения материального баланса и записывается в предположении фильтрации слабосжимаемой жидкости в упругом пласте. В качестве уравнения притока обычно используют формулу Дюпюи или ее аналог в зависимости от конструкции скважины. Как правило, задача рассматривается в однофазной постановке. В зависимости от размеров рассматриваемого в емкостном уравнении объема пласта и учета различных физических явлений выделяют несколько видов CRM-моделей:
- CRMT – Capacitance Resistive Model (Total Field) – для всех скважин рассматривается один поровый объем (Данько и др., 2019; Ручкин и др., 2018; Holanda etal., 2018; Sayarpour, 2008; Sayarpour etal., 2008; Sayarpour et al., 2009; Sayarpour et al., 2010).
- CRMP – Capacitance Resistive Model (Producer-injectors) – у каждой добывающей скважины свой дренируемый поровый объем. Нагнетательная скважина влияет на поровые объемы одной или нескольких добывающих скважин (Ручкин и др., 2018; Lasdon etal., 2017; Holanda etal., 2018; Sayarpour, 2008; Степанов, Поспелова, 2019; Olenchikov, Posvyanskii, 2019; Sayarpour et al., 2009; Sayarpour et al., 2010).
- CRMIP – Capacitance Resistive Model (Injector-Producer Pair) – отдельно рассматриваются общие поровые объемы каждой пары взаимодействующих скважин – добывающая и нагнетательная (Хатмуллин и др., 2018; Holandaetal., 2018; Sayarpour, 2008; Sayarpour et al., 2009).
- CRM Omega – Capacitance Resistive Model (Omega) – модификация CRMIP с учетом поправок на продуктивность при пусках и остановках скважин для учета нестационарности потока (Хатмуллин и др., 2018).
- CRMs – Capacitance Resistive Model (simulator) – каждая скважина (как добывающая, так и нагнетательная) имеет свой поровый объем. Поровые объемы взаимодействуют. Есть учет двухфазного потока нефть – вода и аквифера. Учитывается нестационарный приток при пусках и остановках. Используется численное решение дифференциальных уравнений (Olenchikov, Posvyanskii, 2019).
- CRM-Block– Capacitance Resistive Model (Blocks in series) – расширение моделей CRMT или CRMIP для повышения детальности расчетов. Общий дренируемый объем взаимодействующих скважин разделяется на несколько блоков, выстроенных в линию с последовательным перетоком жидкости из одного в другой. В результате получается квазидвумерная модель (Holanda et al., 2018; Sayarpour, 2008).
- ML-CRM – Capacitance Resistive Model (Multi-Layer inparallel) – многопластовая модель, предполагающая вскрытие парой взаимодействующих скважин нескольких изолированных друг от друга пропластков (Holandaet al., 2018; Степанов и др., 2021; Azadeh Mamghaderi, Peyman Pourafshary, 2013; Seng Wang et al., 2023).
- CRMT-M, CRMP-M иCRMIP-M – Capacitance Resistive Model (Total field – Modified), Capacitance Resistive Model (Producer-injectors – Modified) иCapacitance Resistive Model (Injector-Producer Pair – Modified) – модификация моделей CRMT, CRMP и CRMIP для случая наличия в пласте системы газ – нефть (Yousefi et al., 2019; Sayarpour, 2008).
Преимуществом CRM-моделей перед полномасштабными дискретными численными гидродинамическими моделями является относительная простота и, как следствие, многократно более высокая скорость вычислений. Это позволяет легко использовать CRM-модели в повседневной практике как для анализа и контроля разработки, так и для решения оптимизационных задач.
Преимуществом CRM-моделей перед другими типами моделей является исключение из рассмотрения пластового давления, информация о котором обычно носит несистемный, разрозненный, а часто и недостоверный характер. С ухудшением качества разрабатываемых запасов, наблюдаемым в России, на практике количество определений пластового давления методами восстановления и падения забойного давления неуклонно снижается. Это связано с тем, что такие виды исследований в низкопроницаемых коллекторах и в коллекторах, насыщенных высоковязкой нефтью, требуют остановки скважин на длительный период, что приводит к большим потерям в добыче нефти. В подобных случаях на практике преобладают приближенные методы, позволяющие оценить, но не определить пластовое давление.
Настоящая работа посвящена моделированию взаимодействия скважин при заводнении нефтяного пласта с двойной проницаемостью (слоисто-неоднородный пласт) в рамках CRM-концепции, поэтому рассмотрим подробнее модели типа ML-CRM.
В монографии (Степанов и др., 2021) рассмотрена модель ML-CRM в приближении укрупненных скважин, т.е. обобщена на случай многослойной системы модель CRMT. Это довольно грубый подход, поэтому он для нас не очень интересен, но его следует упомянуть, как редкую публикацию на тему ML-CRM на русском языке.
В работе (Azadeh Mamghaderi, Peyman Pourafshary, 2013) подход CRM к моделированию однослойного коллектора расширен для моделирования слоистого коллектора. В этой модели учитывается переток между пластами. На первом этапе вычислений авторами предлагается пренебрегать эффектами перетока, чтобы получить первоначальное решение и оценить коэффициенты модели, что позволяет увеличить скорость вычислений и перейти к более надежным ответам. В дальнейшем уравнения предложенной модели модифицируются для учета перетока. Утверждается, что при таком подходе сходимость решения происходит быстрее. Далее результаты разработанной модели объединяются с моделью двухфазного потока и представляются в виде кривых зависимости добычи жидкости или нефти от времени для каждой скважины в каждом слое отдельно.
В работе (Seng Wang et al., 2023) предлагается многослойная CRM-модель для определения межскважинной связи внутри каждого слоя с использованием неполных знаний о профилях закачки или добычи. Все известные профили вводятся в модель напрямую, тогда как неизвестные профили других скважин оцениваются путем сопоставления с историческими данными добычи. На основе нейронной сети типа «Долгая краткосрочная память» (LSTM – Long short-term memory) в (Seng Wang et al., 2023) предлагается метод определения связности скважин с учетом остановки скважины. Модель решается путем объединения эволюционного алгоритма биогеографии (BBO – Biogeography-based optimization) и регрессии методом наименьших квадратов.
Наиболее близким аналогом предлагаемой в настоящей статье модели является модель, рассмотренная в (Holanda et al., 2018). Она, в свою очередь, основана на развитии классической CRMP-модели вида:
![]() (1)
(1)
где qi(t) и pw,i(t) – дебит жидкости и забойное давление i-ой добывающей скважины; t – время; Ni – количество нагнетательных скважин, влияющих на i-ую добывающую; fij – коэффициент влияния j-ой нагнетательной скважины на i-ую добывающую (доля воды, закачиваемой в j-ую нагнетательную скважину, приходящаяся на i-ую добывающую); wj(t) – расход закачиваемой воды в j-ую нагнетательную скважину; τi – константа времени; PIi, ct,i и Vp,i – коэффициент продуктивности по жидкости, суммарная сжимаемость системы пласт – флюид и поровый объем, дренируемый i-ой добывающей скважиной; Mj – количество добывающих скважин, на которые влияет j-ая нагнетательная скважина.
Здесь и далее все уравнения записываются в пластовых условиях.
Специфические параметры CRM-моделей, например такие, как fij, ti и PIi, определяются при решении обратной задачи в процессе адаптации моделей.
ML-CRM в работе (Holanda et al., 2018) записана на основании уравнения (1), составленного для каждого k-ого слоя без учета перетоков между слоями в пределах пласта, но с учетом перетоков между слоями через ствол скважины:
![]()
![]()
![]() (2)
(2)
где qp,i,k(t) – дебит жидкости k-ого слоя i-ой скважины с учетом перетоков в другие слои через ствол скважины (кажущийся дебит слоя); f/j,k – доля воды, закачиваемой в j-ую нагнетательную скважину, приходящаяся на k-ый слой; fij,k – доля воды, закачиваемой в k-ый слой через j-ую нагнетательную скважину, приходящаяся на поровый объем i-ой добывающей скважины; fp,i,k – доля дебита жидкости k-ого слоя в дебите жидкости i-ой добывающей скважины; qi,k(t) – дебит i-ой скважины, приходящийся на k-ый слой, без учета перетоков между слоями через ствол скважины; Qc,i,k(t) – переток жидкости из k-ого слоя в другие слои через ствол i-ой добывающей скважины; Nk – количество слоев.
Работы других авторов, приведенные выше, имеют следующие недостатки, устранению которых посвящена настоящая статья.
- Не учитываются перетоки жидкости между слоями непосредственно в пласте перпендикулярно напластованию.
- При моделировании двухфазной фильтрации используется эмпирический подход, слабо учитывающий влияние изменения режимов работы нагнетательных скважин на характер обводнения.
Материалы и методы
Математическая модель
Рассмотрим авторскую модель взаимодействия скважин при заводнении нефтяного пласта с двойной проницаемостью (слоисто-неоднородный пласт) в рамках концепции CRM-моделирования.
Реальные нефтяные пласты обычно имеют более двух пропластков. Однако из теории упругого режима фильтрации и практики гидродинамических исследований скважин известно, что в большинстве случаев для моделирования упругой фильтрации достаточно двух слоев. Поэтому в статье рассмотрена модель двуслойного пласта. В теории гидродинамических исследований скважин модель двуслойного пласта с перетоками называют моделью двойной проницаемости. В практике численного моделирования разработки нефтяных месторождений под моделью двойной проницаемости понимают другое – модификацию модели двойной пористости. В этой статье мы будем придерживаться терминологии, принятой в области гидродинамических исследований скважин.
Отличия предлагаемой модели от моделей других авторов состоят в следующем.
- Модель учитывает возможные перетоки между слоями за счет вертикальной фильтрации поперек напластования.
- Модель учитывает двухфазный характер фильтрации при заводнении, благодаря использованию дифференциального уравнения сохранения объема воды в пластовых условиях. Такой подход является наиболее точным и физически обоснованным.
- Дифференциальные уравнения модели решаются с помощью численных методов.
- Рассматривается система, состоящая из двух слоев с разными фильтрационно-емкостными свойствами.
Будем считать, что в каждом слое у каждой добывающей скважины есть свой дренируемый поровый объем. Каждая нагнетательная скважина влияет на поровые объемы одной или нескольких добывающих скважин. Таким образом, предлагаемая модель является обобщением модели CRMP на случай двух слоев с перетоками.
Запишем систему уравнений CRM-модели, описывающую работу добывающей скважины в двухслойном пласте в рамках концепции CRMP:
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
где pi,k(t), k = 1, 2 – среднее пластовое давление в объеме дренирования i-ой скважины; qi,12(t) – переток жидкости из первого слоя во второй за счет вертикальной фильтрации поперек напластования; PIi,12 – соответствующий коэффициент перетока; fij,k – доля воды, закачиваемой в пласт через j-ую нагнетательную скважину, приходящаяся на поровый объем k-ого слоя i-ой добывающей скважины, коэффициент переопределен по сравнению с используемым в формуле (2); остальные обозначения соответствуют обозначениям, приведенным к формулам (1) и (2).
Выразив из (5) среднее пластовое давление pi,k(t), получим:
![]() (9)
(9)
Продифференцируем (9) по времени:
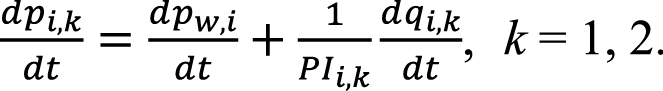 (10)
(10)
Сложим (3) и (4):
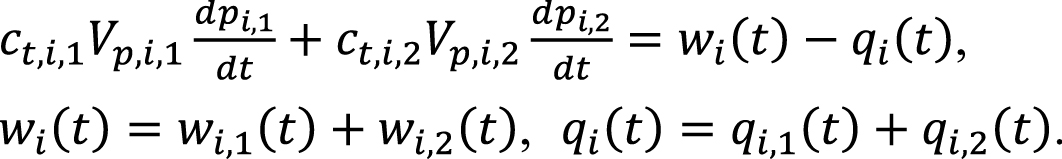 (11)
(11)
Подставим (10) в (11), проведя алгебраические преобразования:
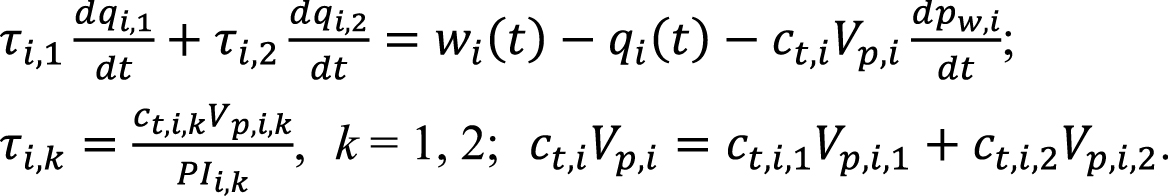 (12)
(12)
Из (7) следует:
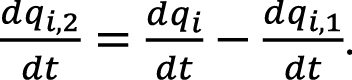 (13)
(13)
Подставим (13) в (12) и получим дифференциальное уравнение для забойного давления pw,i(t) или дебита жидкости qi(t):
![]() (14)
(14)
Подставим (10) в (3):
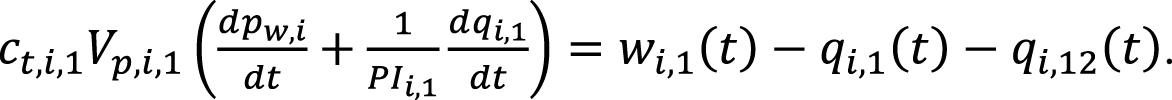 (15)
(15)
Подставим (9) в (6):
![]() (16)
(16)
Выразим qi,2(t) из (7) и подставим в (16), проведя алгебраические преобразования:
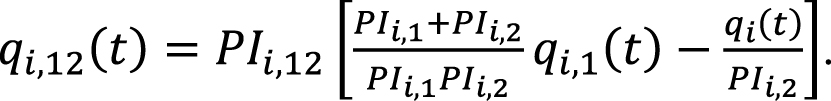 (17)
(17)
Подставим (17) в (15) и, проведя алгебраические преобразования, получим дифференциальное уравнение для дебита жидкости первого слоя qi(t):
![]() (18)
(18)
Для решения дифференциальных уравнений (14) и (18) нужно задать начальные условия для дебита жидкости и забойного давления.
Будем решать уравнения (14) и (18) с помощью численных методов.
Явный метод решения для уравнения (14):
– относительно дебита скважины по жидкости
![]() (19)
(19)
– относительно забойного давления
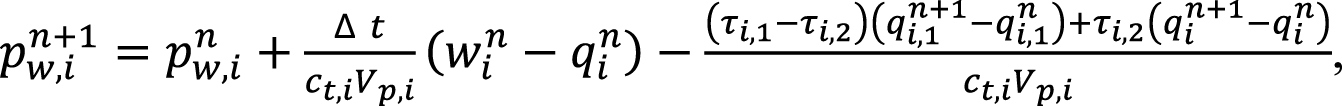 (20)
(20)
где n – номер шага по времени, Δt – размер шага по времени.
Явный метод решения для уравнения (18):
![]() (21)
(21)
Системы уравнений в конечных разностях (19) и (21) или (20) и (21), которые можно использовать для решения системы дифференциальных уравнений (14) и (18), следует дополнить соотношением:
![]() (22)
(22)
Неявный метод решения уравнений (14) и (18):
![]() (23)
(23)
![]() (24)
(24)
Аналогичную систему уравнений можно записать для j-ой нагнетательной скважины.
Тогда в общем случае получаем систему линейных алгебраических уравнений (СЛАУ) относительно переменных qi(t) или pw,i(t), wj(t) или pw,j(t), qi,k(t) и wj,k(t) для k = 1, 2, состоящую из 2(Nprod + Ninj) уравнений, где Nprod – общее количество добывающих скважин, а Ninj – общее количество нагнетательных скважин.
Явный метод решения уравнения для давления является условно устойчивым и требует контроля шага по времени для обеспечения устойчивости решения.
Полностью неявный метод является безусловно устойчивым. Однако все равно необходимо вводить ограничения на шаг по времени, например, для уменьшения погрешности дискретизации.
Перейдем к расчетам обводнения. Для этого запишем дифференциальное уравнение сохранения объема воды в пластовых условиях для отдельной скважины в предположении упругого пласта и малой сжимаемости воды:
![]() (25)
(25)
где знак плюс берется для второго слоя (k = 2), а знак минус – для первого (k = 1), Vw,i,k – объем воды в зоне дренирования i-ой скважины в k-ом слое, qw,i,k(t) – дебит воды i-ой скважины в k-ом слое, Fi,12(t) – доля воды в потоке из одного слоя в другой.
С другой стороны, в заданных условиях объем воды в отдельном слое можно определить способом, описанным в работе (Афанаскин, 2016). Обобщим формулу из этой работы на случай двуслойного пласта:
![]() (26)
(26)
где Vp,i,k – поровый объем (объем дренирования) i-ой скважины в k-ом слое, cr,i,k – сжимаемость породы в объеме дренирования i-ой скважины в k-ом слое, cw – сжимаемость воды, si,k(t) – водонасыщенность в объеме дренирования i-ой скважины в k-ом слое.
Приравнивая выражения (25) и (26), после некоторых преобразований получим дифференциальное уравнение для водонасыщенности:
![]() (27)
(27)
Подставим (10) в (27) и воспользуемся явным численным методом:
![]() (28)
(28)
Доля воды в потоке из одного слоя в другой определяется методом «вверх по потоку»:
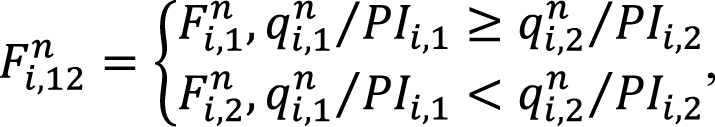 (29)
(29)
где Fi,1n и Fi,2n – доля воды в потоке в слое 1 и 2 соответственно, т.е. функция Бакли – Леверетта (Басниев и др., 1993), которая вычисляется как:
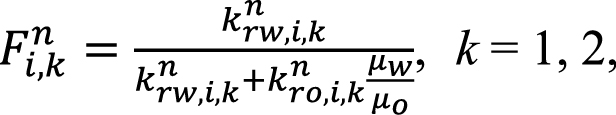 (30)
(30)
где krα,i,kn (α = o, w и k = 1, 2) – относительная фазовая проницаемость фазы α, являющаяся однозначной заданной функцией давления; µα (α = o, w) – динамическая вязкость фазы α.
Дебиты по фазам рассчитываются следующим образом:
![]() (31)
(31)
Явный метод решения уравнения для насыщенности является условно устойчивым и требует контроля шага по времени для обеспечения устойчивости решения. Насыщенность на новом шаге по времени рассчитывается после расчета давления.
При расчете давления изменение суммарной сжимаемости системы пласт-флюид в результате изменения насыщенности не учитывается. При расчете насыщенности учитываются сжимаемости пласта и флюида.
Модель калибруется на данные промыслово-геофизических исследований (ПГИ) и историю разработки. В отсутствие данных ПГИ в качестве нулевого приближения можно использовать данные численного моделирования из гидродинамических симуляторов (в этом случае нужно знать длительную историю обводнения с отражением на ней послойного обводнения).
Полученная модель легко обобщается на случай переменного по времени коэффициента продуктивности по жидкости. Это может понадобиться при переменном скин-факторе или в случае, когда коэффициент продуктивности существенно зависит от обводненности.
Результаты
Тестирование на модельных данных
Рассмотрим применение предложенной модели на модельных данных. Преимуществом модельных данных является тот факт, что мы достоверно знаем как исходные данные (параметры пласта, скважин и жидкостей), так и все показатели разработки. Для получения модельных данных использовался трехмерный гидродинамический симулятор tNavigator компании RFD (Россия). Модель двухфазная – нефть и вода.
В модельном примере рассматривается взаимодействие четырех скважин – двух добывающих (P1 и P2) и двух нагнетательных (I1 и I2), рис. 1. Изучаются показатели разработки двух добывающих скважин.
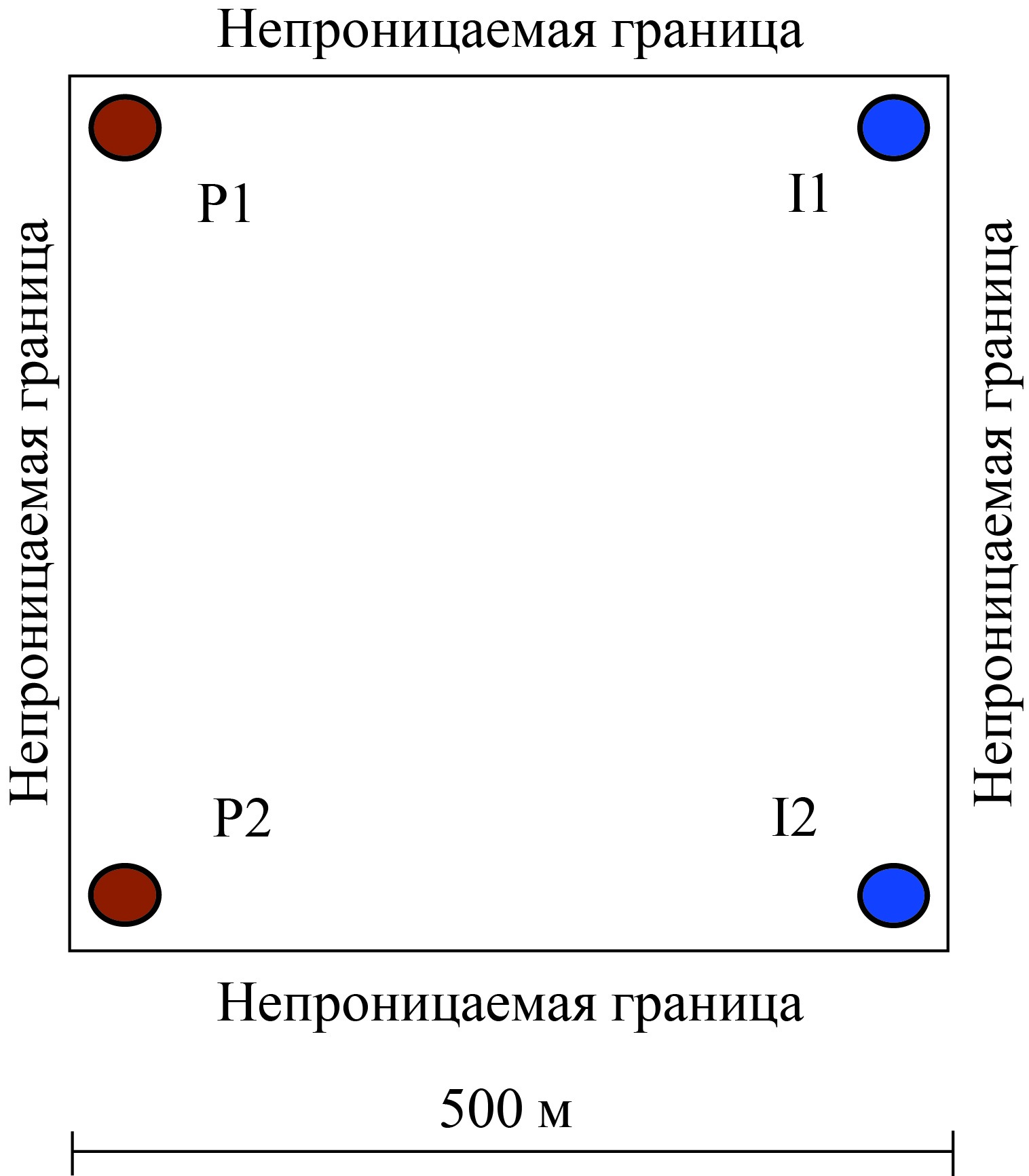
Рис. 1. Расположение скважин и границ в модельном примере
Параметры гидродинамической модели:
- Количество ячеек по осям X х Y х Z – 20 х 20 х 2 шт.
- Размеры ячеек по осям X х Y х Z – 25 х 25 х 10 м.
- Глубина кровли пласта – 2859.3 м.
- Начальное пластовое давление и температура (на кровле пласта) – 285.9 бар и 92.2 °С.
- Проницаемость верхнего слоя – 100 мД.
- Проницаемость нижнего слоя – 10 мД.
- Пористость – 0.18 д.ед.
- Коэффициент вертикальной анизотропии проницаемости – 0.1 д.ед.
- Свойства воды: объемный коэффициент – 1.02 м3/м3, вязкость – 0.33 мПа·с, сжимаемость – 4.1·10-5 1/бар.
- Свойства нефти: объемный коэффициент – 1.162 м3/м3, вязкость – 0.62 мПа·с, сжимаемость – 1.3·10-4 1/бар, газосодержание – 73.4 м3/м3, давление насыщения – 98.2 бар.
- Сжимаемость пласта – 4.3·10-5 1/бар.
- Начальная водонасыщенность – 0.34 д.ед.
- Относительные фазовые проницаемости приведены на рис.2.
- Скважины вскрывают оба слоя.
- Добывающие скважины работают при заданном дебите жидкости (меняется один раз в месяц) и ограничены минимальным забойным давлением 98.2 бар, равным давлению насыщения.
- Нагнетательные скважины работают при заданном постоянном забойном давлении 335.9 бар (начальное пластовое давление плюс 50 бар репрессии).
- Срок разработки – 20 лет.
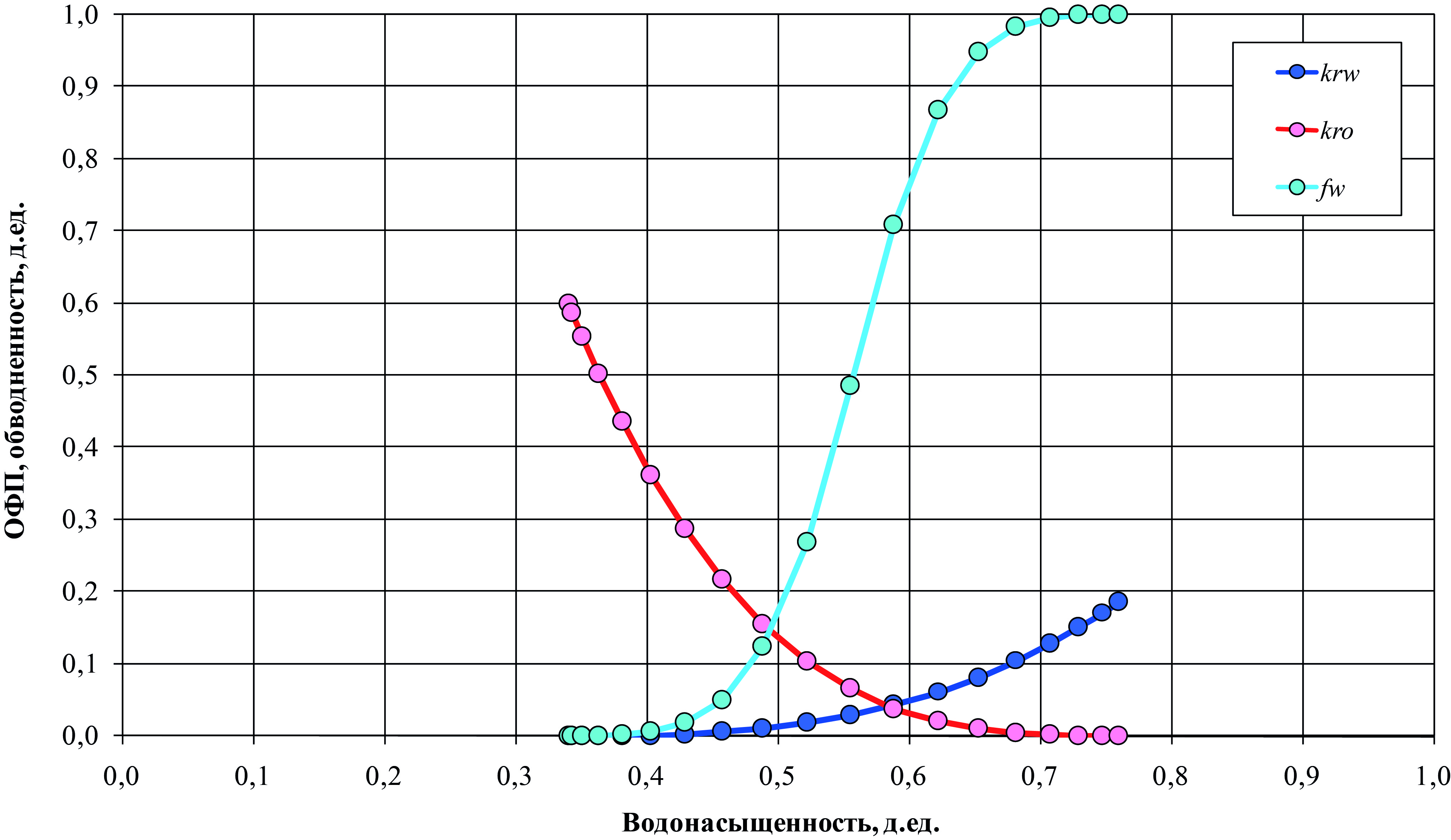
Рис. 2. Относительные фазовые проницаемости по воде (krw) и нефти (kro),
обводненность (fw), как функции водонасыщенности в модельном примере
Дебит добываемой жидкости и расход закачиваемой воды приведены на рис. 3. Забойные давления в добывающих скважинах приведены на рис. 4. Доля дебита жидкости из второго (низкопроницаемого) слоя приведена на рис. 5. Обводненность продукции добывающих скважин приведена на рис. 6.
Рис. 3. Дебит добываемой жидкости и расход закачиваемой воды в модельном примере
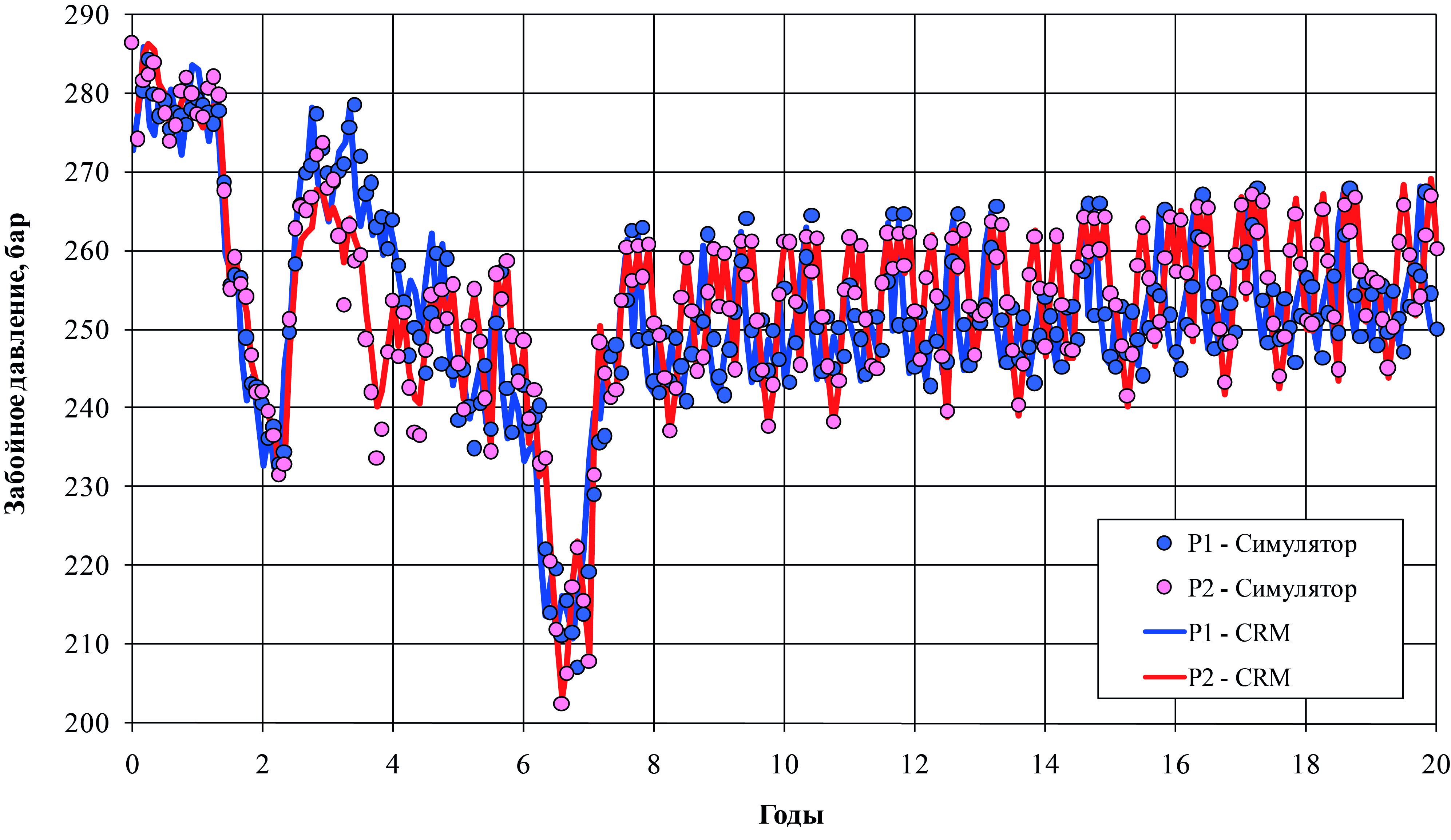
Рис. 4. Забойное давление в добывающих скважинах в модельном примере
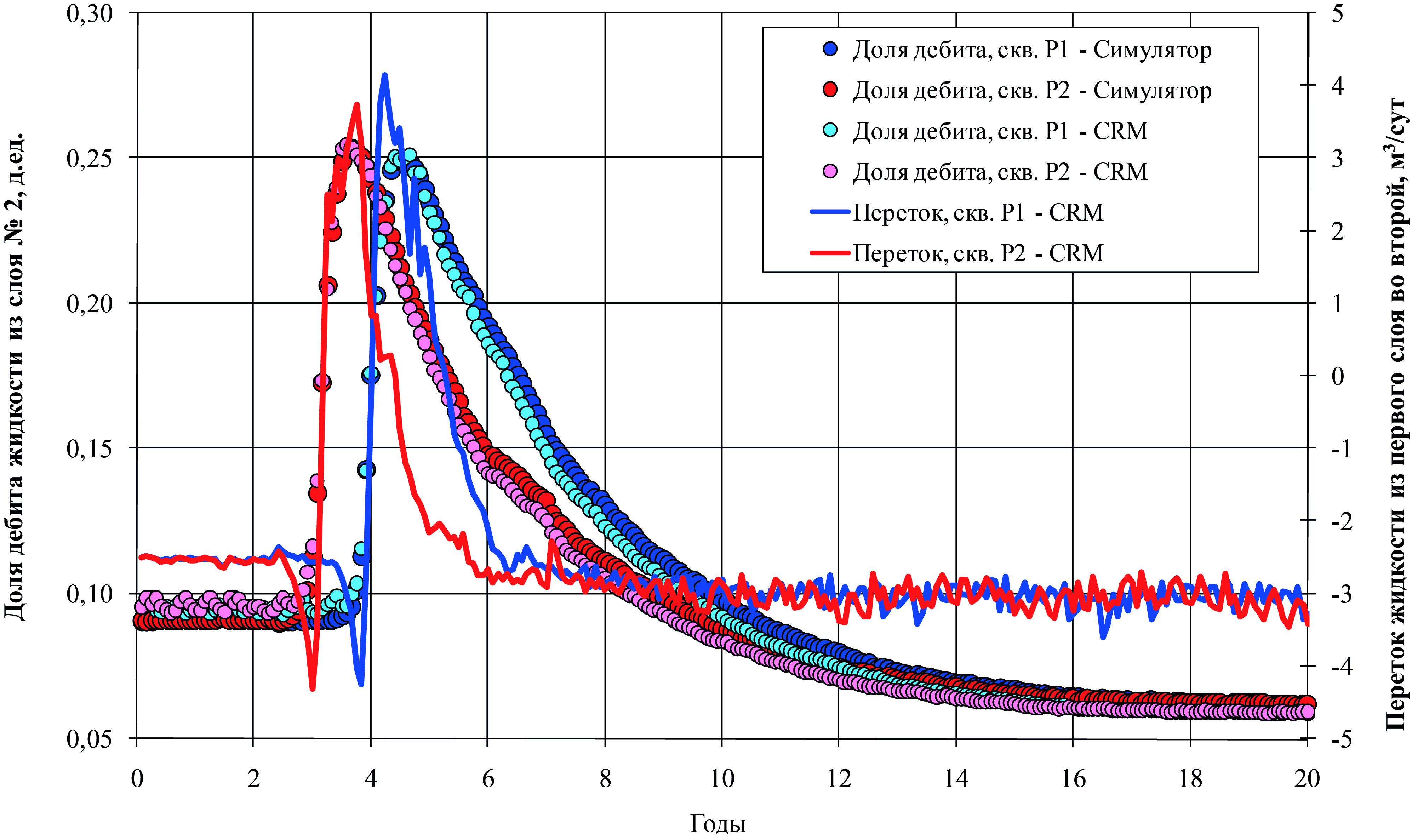
Рис. 5. Доля дебита жидкости из второго (низкопроницаемого) слоя в модельном примере
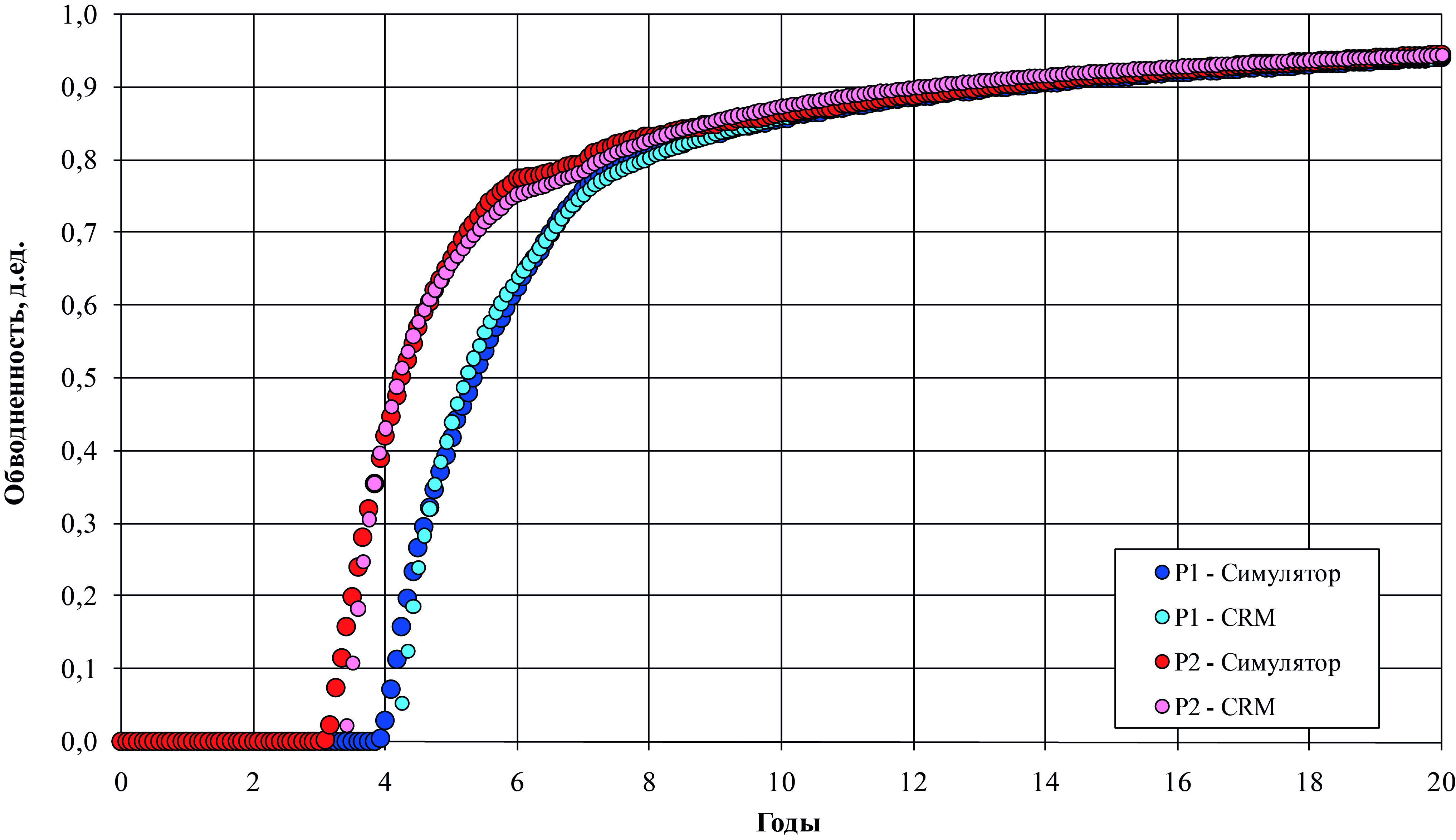
Рис. 6. Обводненность продукции добывающих скважин в модельном примере
Тестирование на фактических данных
Рассмотрим использование предложенной модели на фактических данных. Это необходимо, поскольку в конечном счете нас интересует практическая применимость предлагаемой модели. Очевидно, что точность расчетов на фактических данных должна быть меньше, чем на модельных. В разделе «Обсуждение результатов» этот вопрос комментируется более подробно.
В качестве примера рассмотрим показатели разработки добывающих скважин №№ 484 и 499, вскрывающих пласт Ач3 одного из нефтяных месторождений Западной Сибири. Будем также учитывать работу окружающих скважин. Всего на пласт работает 50 скважин. Фильтрационно-емкостные свойства пласта Ач3 в пределах водо-нефтяного контакта (ВНК) представлены в табл. 1. Коэффициент анизотропии вертикальной проницаемости принят 0.1 д.ед. В качестве примера распределения проницаемости и пористости по толщине пласта на рис. 7 приведено распределение в районе скважины № 484.

Табл. 1. Фильтрационно-емкостные свойства пласта Ач3 в пределах ВНК
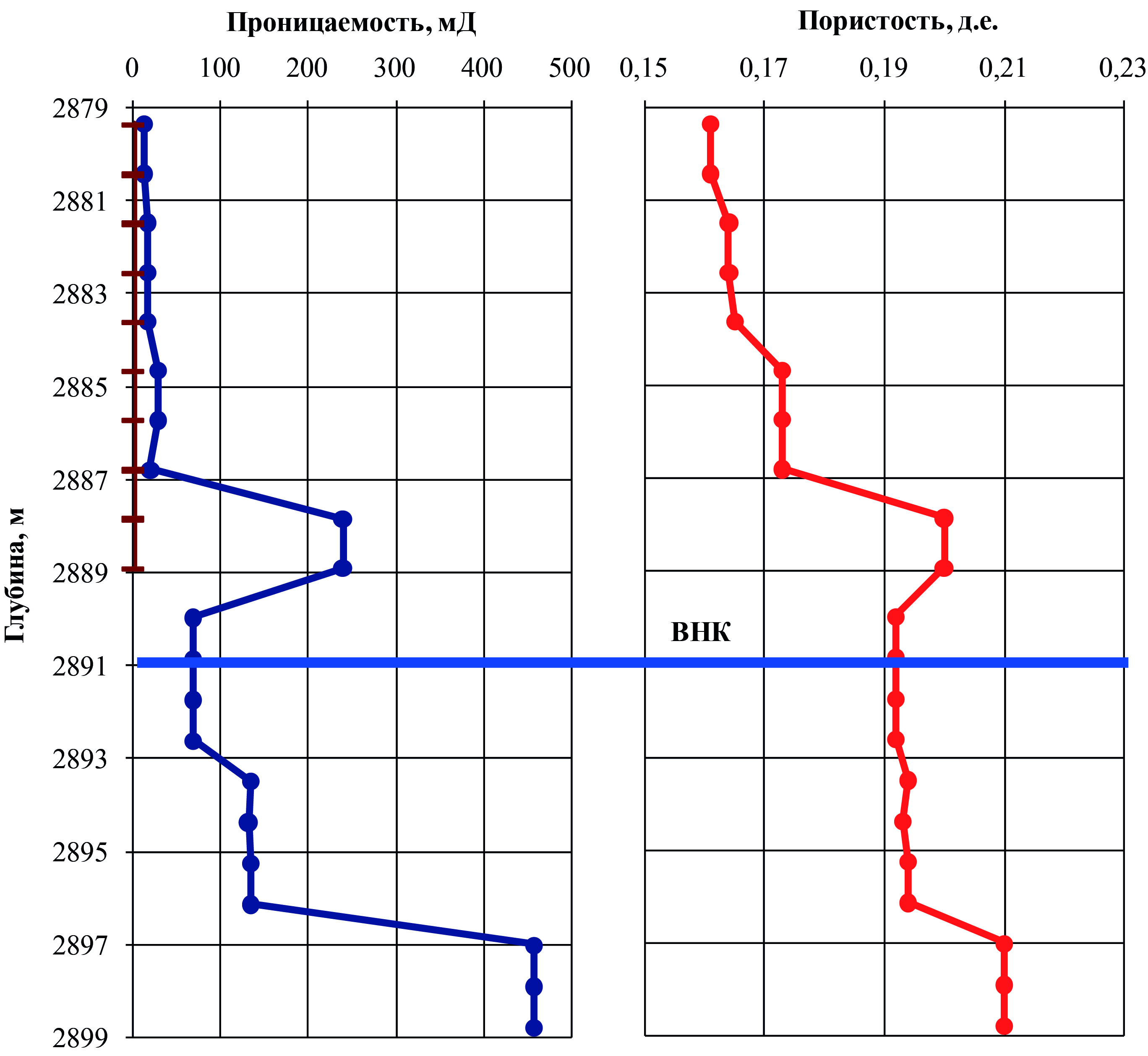
Рис. 7. Распределение проницаемости и пористости по толщине пласта
в районе скважины № 484 в фактическом примере
Залежь нефти пластового типа тектонически ограничена с двух сторон. Коллектор терригенный. Уровень ВНК – 2891 м. Начальное пластовое давление на ВНК – 255 бар. Начальная пластовая температура, свойства нефти и воды совпадают с описанными в предыдущем разделе «Тестирование на модельных данных».
Изучаемая скважина № 484 находится в центральной части ловушки, окружена добывающими скважинами №№ 482, 485, 487, 494, 495, 496 и водонагнетательными скважинами № 66 и 480 (рис. 8).
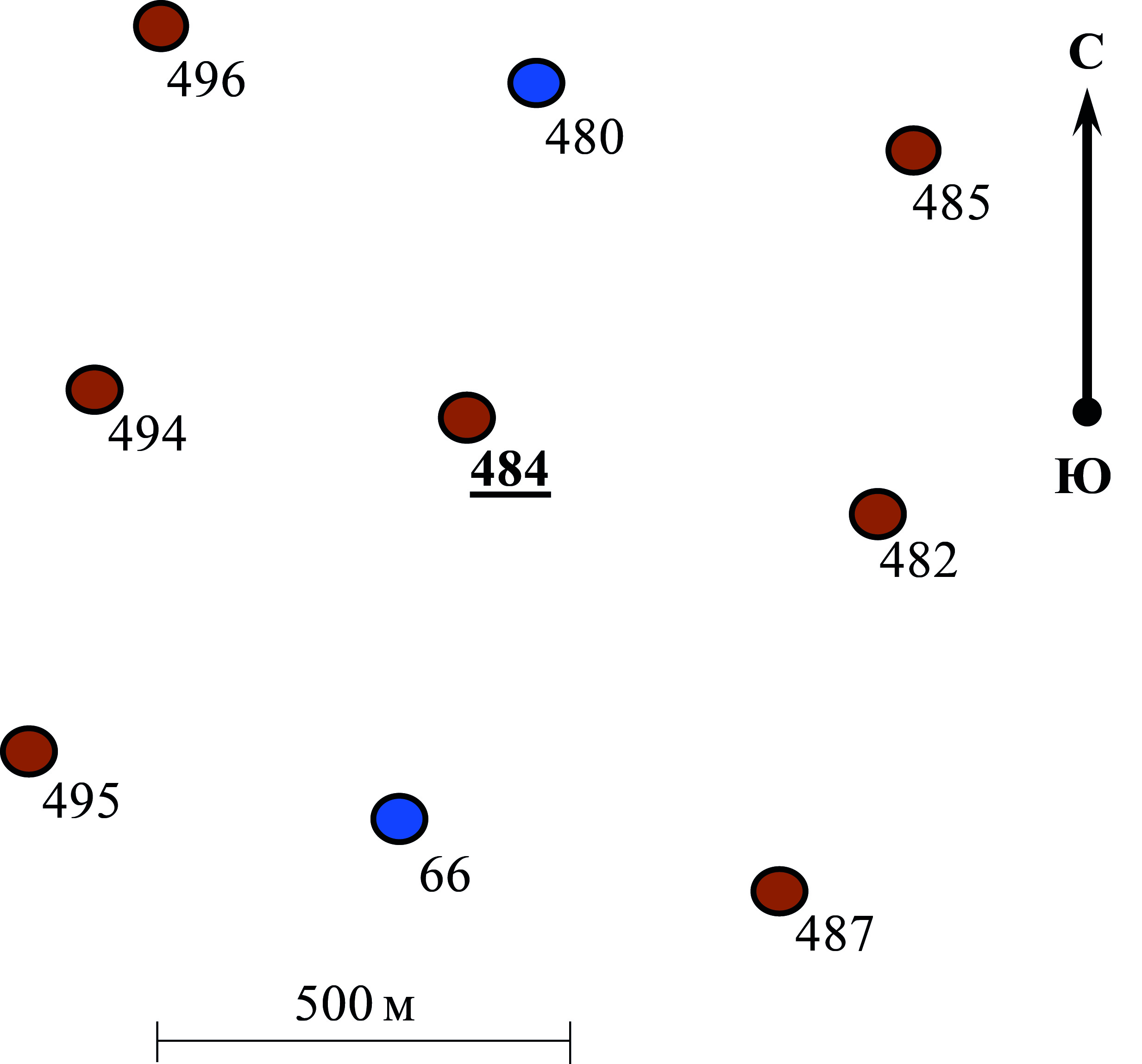
Рис. 8. Расположение скважин в фактическом примере, район скважины № 484
Изучаемая скважина № 499 находится в краевой зоне, окружена добывающими скважинами №№ 481, 483, 498, 774 и водонагнетательной скважиной № 486 (рис. 9).
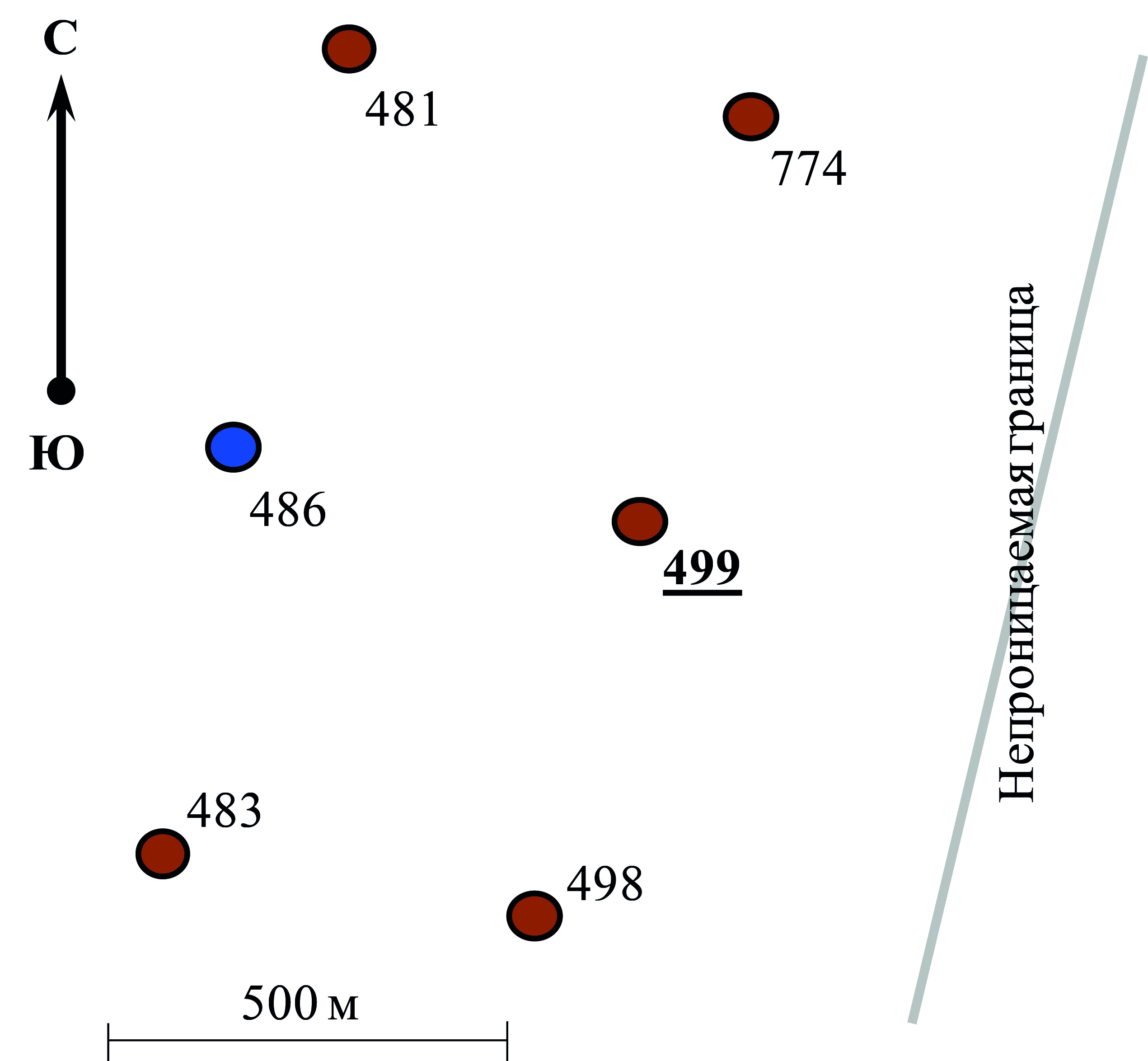
Рис. 9. Расположение скважин и границ в фактическом примере,
район скважины № 499
Относительные фазовые проницаемости приведены на рис. 10. История работы исследуемых скважин и их окружения приведена на рис. 11 и 12. Забойные давления в добывающих скважинах приведены на рис. 13. Обводненность продукции добывающих скважин приведена на рис. 14.
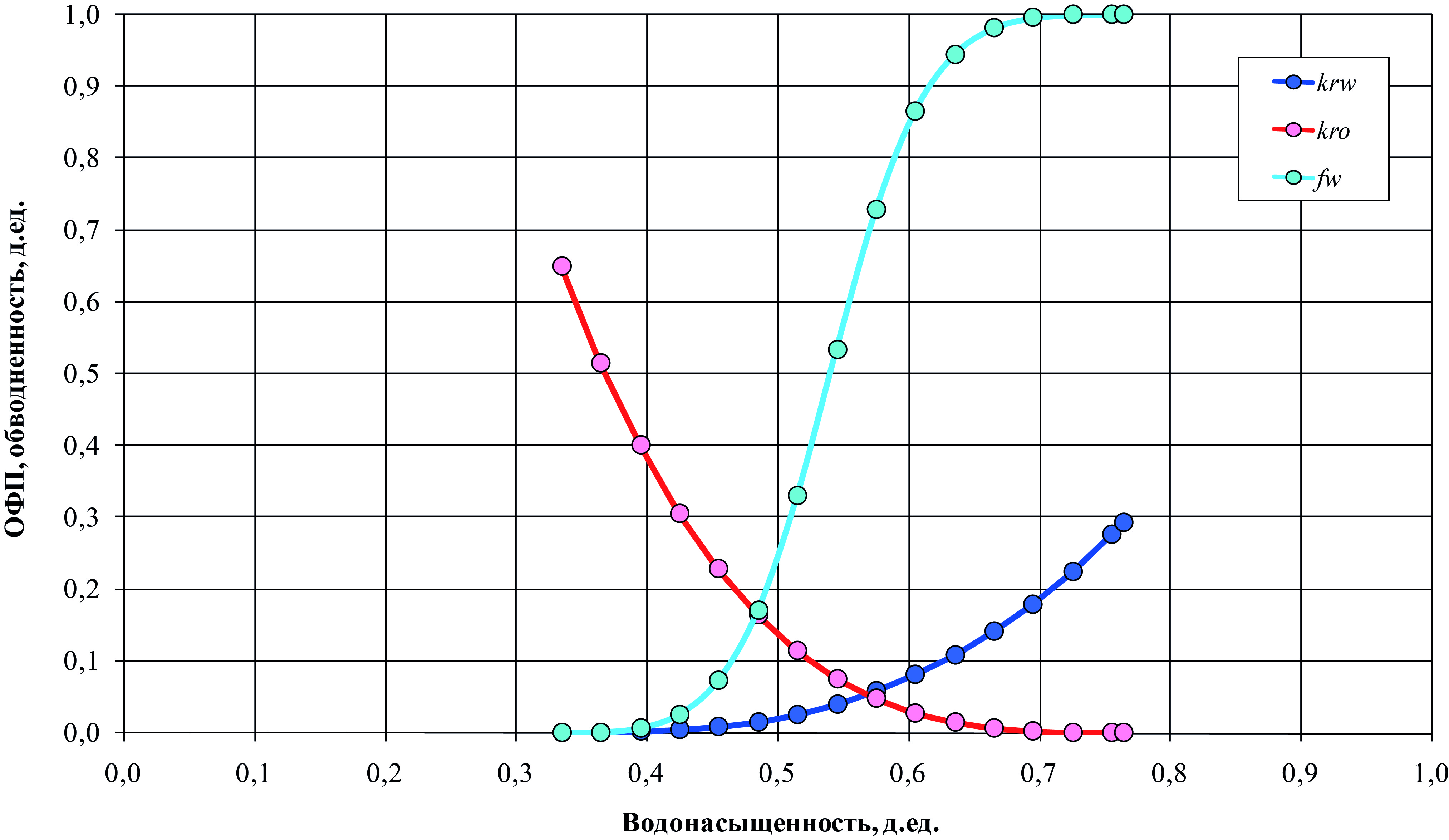
Рис. 10. Относительные фазовые проницаемости по воде (krw) и нефти (kro),
обводненность (fw), как функции водонасыщенности в фактическом примере
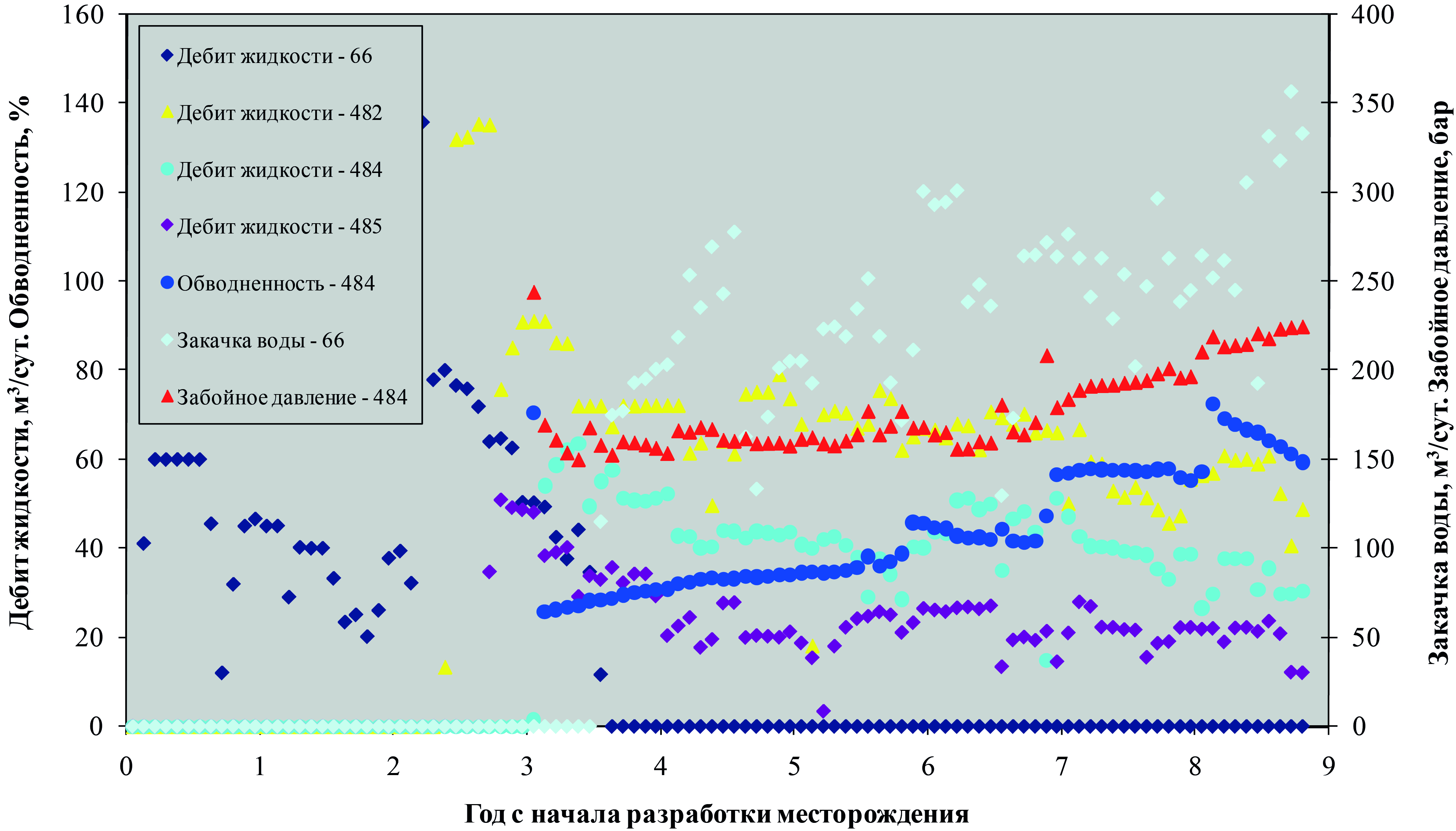
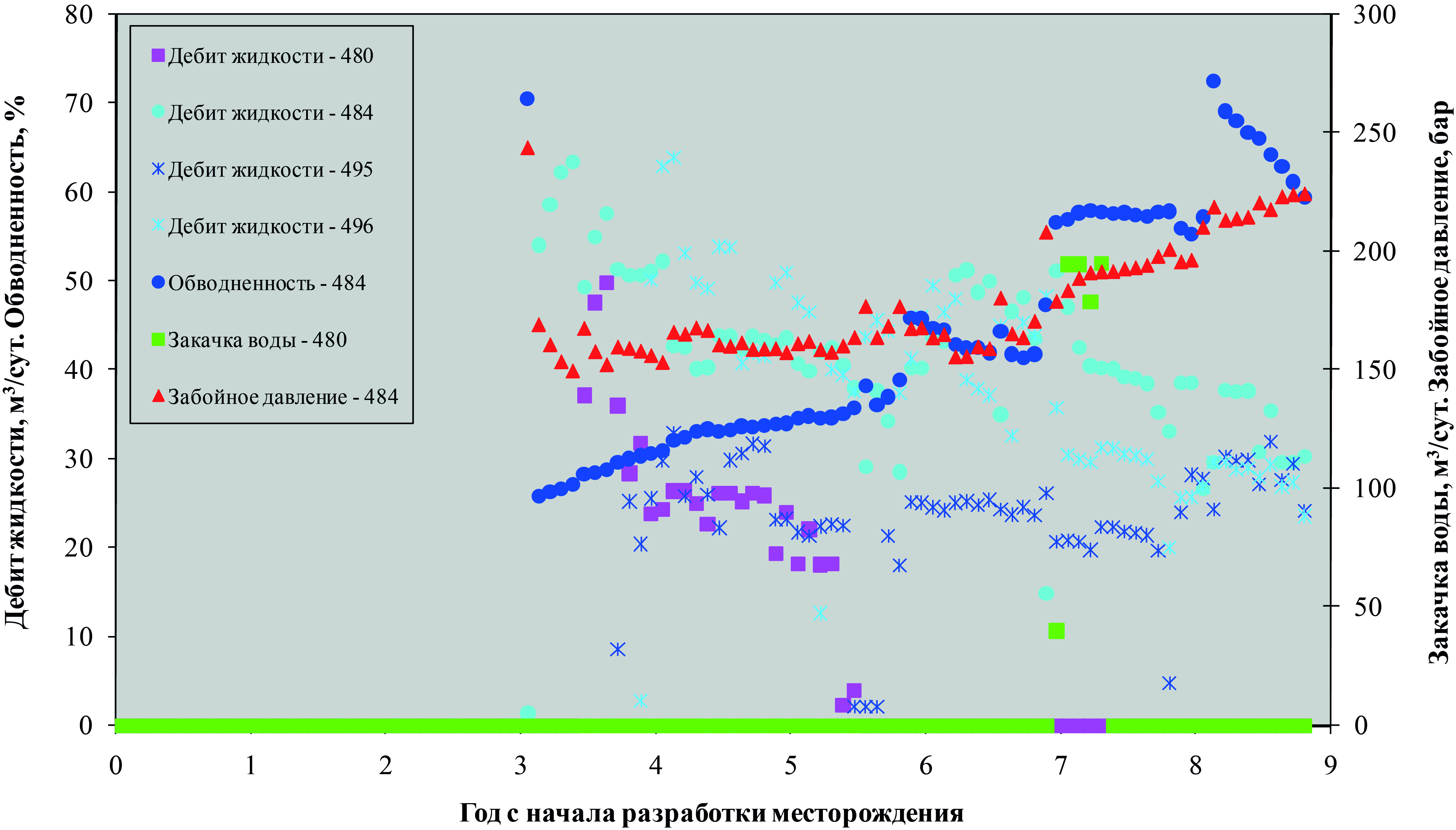
Рис. 11. История работы скважины № 484 и окружающих ее скважин:
А) скв. №№ 66, 482, 484, 485; Б) скв. №№ 480, 484, 495, 496,
фактический пример
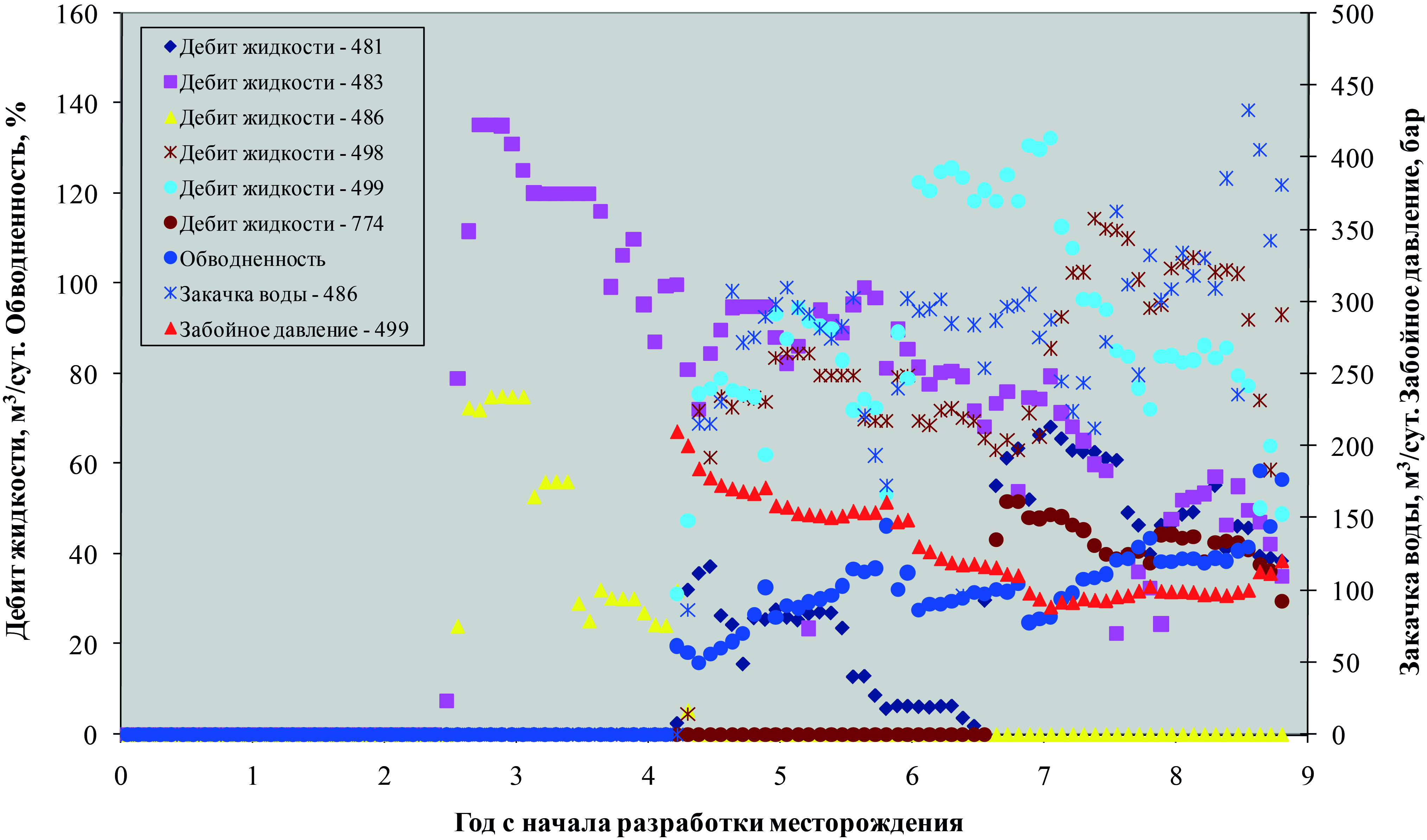
Рис. 12. История работы скважины № 499 и окружающих ее скважин,
фактический пример
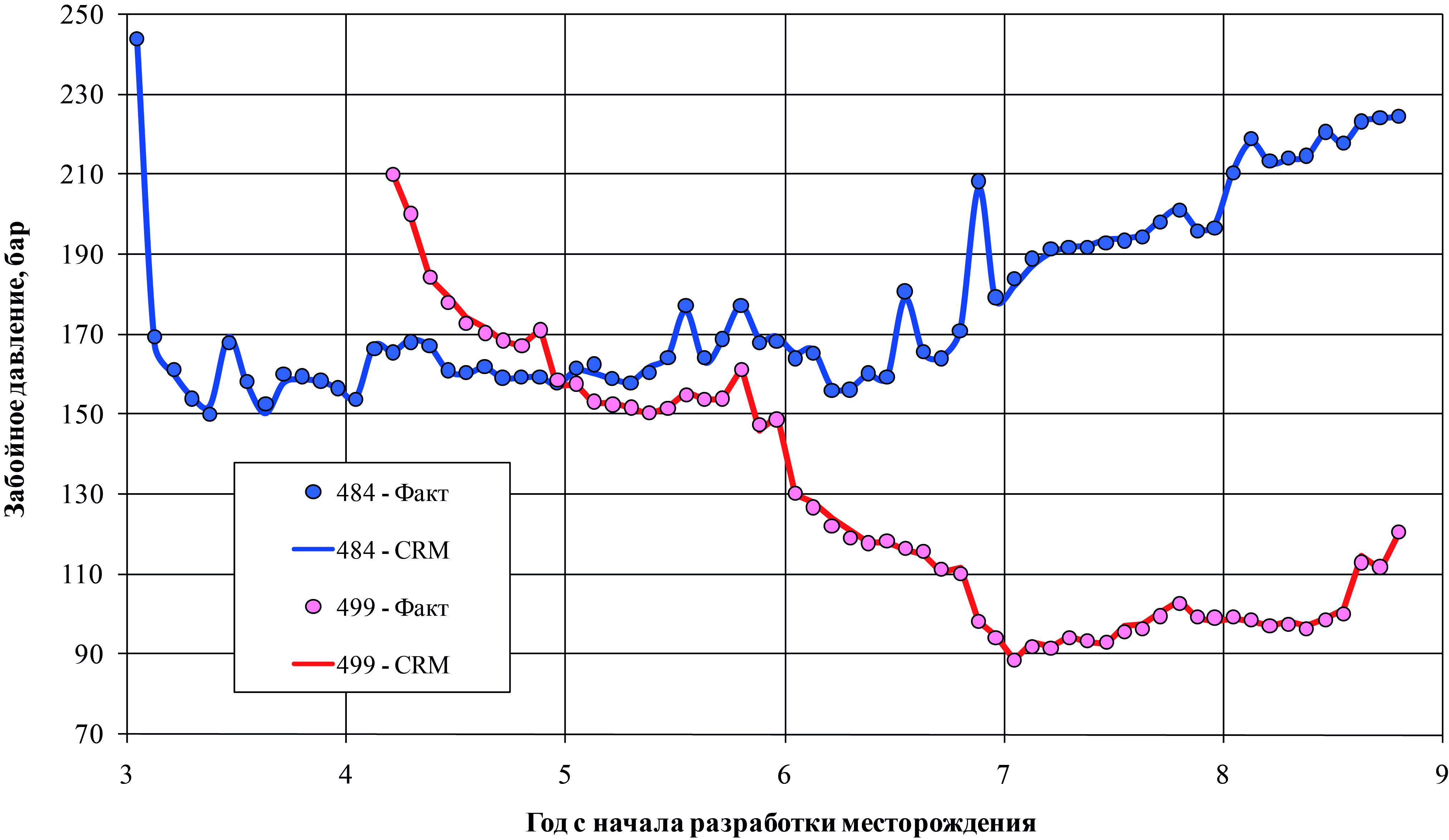
Рис. 13. Забойное давление в добывающих скважинах в фактическом примере
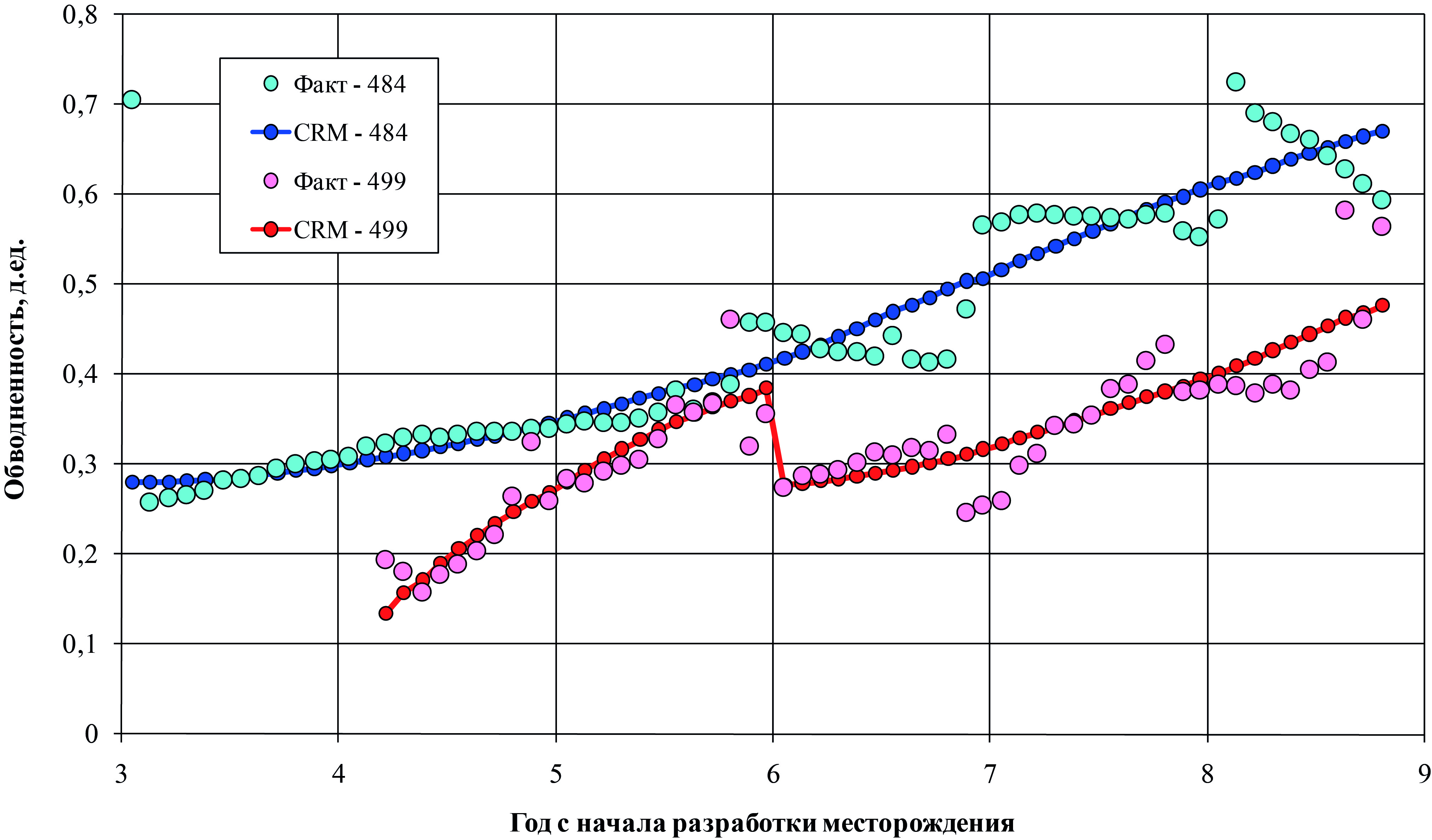
Рис. 14. Обводненность продукции в добывающих скважинах в фактическом примере
Обсуждение результатов
В модельном примере дебиты жидкости добывающих скважин были получены с помощью генератора случайных чисел (рис. 3). Нагнетательные скважины работают при заданном постоянном забойном давлении. При этом расчетный расход закачиваемой воды в этих нагнетательных скважинах изменяется периодическим (регулярным) образом. Это объясняется тем, что они реагируют на изменение дебита жидкости добывающих скважин в результате интерференции (рис. 3).
Каждая нагнетательная скважина один раз за историю разработки останавливается на несколько месяцев для внесения более существенной нестационарности в показатели разработки и создания сложной гидродинамической картины потоков в пласте (рис. 3).
На рис. 4 приведены забойные давления в добывающих скважинах, рассчитанные с помощью трехмерного гидродинамического симулятора и предлагаемой CRM-модели. Видно хорошее совпадение кривых: для скважины P1 получен коэффициент детерминации R2 = 0.9780, а для скважины P2 – R2 = 0.9846 (коэффициент детерминации R2 – доля дисперсии зависимой переменной, объясняемая принятой моделью).
Доля дебита жидкости из второго (низкопроницаемого) слоя в модельном примере, полученная с помощью CRM-модели, имеет большие колебания, чем рассчитанная с помощью симулятора (рис. 5). Однако видно хорошее совпадение кривых, полученных с помощью симулятора и CRM-модели: для скважины P1 получен коэффициент детерминации R2 = 0.9841, а для скважины P2 – R2 = 0.9822.
В модельном примере обводненность продукции добывающих скважин, полученная с помощью CRM-модели, хорошо согласуется с обводненностью, рассчитанной с помощью симулятора (рис. 6). Для скважины P1 получен коэффициент детерминации R2 = 0.9621, а для скважины P2 – R2 = 0.9259.
В результате получаем, что в модельном примере при сравнении различных показателей разработки, рассчитанных с помощью CRM-модели и с помощью гидродинамического симулятора, коэффициент детерминации R2 составляет не менее 0.9. Это является хорошим результатом и говорит о высоком уровне совпадения кривых, рассчитанных двумя указанными способами.
Модель хорошо учитывает возможные перетоки между слоями за счет вертикальной фильтрации поперек напластования, что следует из наличия скачка на рис. 5. Скачок доли дебита жидкости из слоя 2 (низкопроницаемого) на рис. 5 связан с перераспределением жидкости между слоями при остановке закачки воды в скважину I1 и падением забойного давления в добывающих скважинах. При этом пластовые давления в слоях не равны из-за неравномерной выработки. Остановка нагнетательной скважины I2 уже не дает скачка, но меняет крутизну тренда. Также на рис. 5 приведен переток жидкости из первого слоя во второй. Видно, что на самом деле большую часть времени жидкость перетекает из второго слоя в первый. Из рисунка видно, что 10 % дебита второй слой отдает непосредственно через стенку скважины, и еще 6 % добывается за счет перетока жидкости поперек напластования из второго слоя в первый. Всего второй слой дает 16 % дебита жидкости.
В фактическом примере рассмотрены две добывающие скважины, расположенные в разных зонах продуктивного пласта реального нефтяного месторождения. При расчетах показателей разработки учтено влияние ближайших окружающих скважин.
На рис. 13 приведены фактические и рассчитанные с помощью предлагаемой CRM-модели забойные давления в добывающих скважинах. Видно хорошее совпадение кривых: для скважины № 484 получен коэффициент детерминации R2 = 0.9884, а для скважины № 499 – R2 = 0.9894.
В фактическом примере обводненность продукции добывающих скважин, полученная с помощью CRM-модели, хорошо согласуется с фактической обводненностью (рис. 14). Для скважины № 484 получен коэффициент детерминации R2 = 0.7845, а для скважины № 499 – R2 = 0.8095.
В результате получаем, что в фактическом примере при сравнении рассчитанных с помощью CRM-модели и фактических показателей разработки коэффициент детерминации R2 составляет не менее 0.7 (здесь специально применено округление в меньшую сторону). Это является хорошим результатом для фактических данных и говорит о высоком уровне совпадения расчетных и фактических кривых.
Рассматривая оба примера вместе, можно сделать следующий вывод: в результате тестирования на фактических данных ожидаемо получены коэффициенты детерминации меньше, чем при тестировании на модельном примере. Это вызвано многими причинами, главные из них – погрешности в определении свойств пласта и флюидов, погрешности при замерах показателей разработки, влияние сложных нелинейных процессов, многие из которых отсутствуют в гидродинамических моделях и CRM-моделях, сложность геологического строения, влияние неоднородности пласта и др.
Заключение
В работе предложена модель взаимодействия скважин при заводнении слоисто-неоднородного нефтяного пласта в рамках концепции CRM-моделирования. Отличия предлагаемой модели от моделей других авторов состоят в следующем.
- Благодаря учету механизма вертикальной фильтрации модель принимает во внимание внутрипластовые перетоки между слоями.
- С помощью дифференциального уравнения сохранения объема воды моделируется процесс двухфазной фильтрации, развивающийся при заводнении. Это делает принятый в работе подход к учету двухфазного характера потока жидкости в пласте наиболее точным и физически обоснованным.
- Для решения дифференциальных уравнений модели применяются численные методы.
- Продуктивный нефтяной пласт в модели представлен системой, состоящей из двух слоев, обладающих различными фильтрационными и емкостными характеристиками.
Рассмотрены два метода решения системы уравнений.
- Полностью явный метод решения уравнений для давления и насыщенности является условно устойчивым и требует контроля шага по времени для обеспечения устойчивости решения.
- Неявный по давлению и явный по насыщенности метод также является условно устойчивым, но позволяет использовать большие шаги по времени.
Проведено тестирование предложенной модели на фактических и модельных (полученных с помощью трехмерного гидродинамического симулятора) данных.
В модельном примере при сравнении различных показателей разработки, рассчитанных с помощью CRM-модели и с помощью гидродинамического симулятора, коэффициент детерминации R2 составляет не менее 0.9. Это является хорошим результатом и говорит о высоком уровне совпадения кривых, рассчитанных двумя указанными способами.
В фактическом примере при сравнении рассчитанных с помощью CRM-модели и фактических показателей разработки коэффициент детерминации R2 составляет не менее 0.7. Это является хорошим результатом для фактических данных и говорит о высоком уровне совпадения расчетных и фактических кривых.
По результатам тестирования можно рекомендовать предлагаемую модель для практического использования при изучении взаимодействия скважин в процессе заводнения слоисто-неоднородного нефтяного пласта в рамках концепции CRM-моделирования.
Финансирование/Благодарности
Исследование выполнено за счет гранта Российского научного фонда № 22-77-10081, https://rscf.ru/project/22-77-10081/
Авторы выражают большую благодарность анонимным рецензентам за ценные замечания и предложения, которые способствовали улучшению работы.
Список литературы
1. Афанаскин И.В. (2016). Адресная оценка эффективности реализуемых систем разработки нефтяных месторождений. Геология, геофизика и разработка нефтяных и газовых месторождений, 8, с. 44–54.
2. Басниев К.С., Кочина И.Н., Максимов В.М. (1993). Подземная гидродинамика. М.: Недра, 416 с.
3. Данько М.Ю., Бриллиант Л.С., Завьялов А.С. (2019). Применение метода динамического материального баланса и CRM-метода (Capacitance-Resistive Model) к подсчету запасов ачимовских и баженовских коллекторов. Недропользование XXI век, 4(50), с. 76–85.
4. Ручкин А.А., Степанов С.В., Князев А.В. и др. (2018). Исследование особенностей оценки взаимовлияния скважин на примере модели CRM. Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика, 4(4), с. 148–168. https://doi.org/10.21684/2411-7978-2018-4-4-148-168
5. Степанов С.В., Бекман А.Д., Ручкин А.А., Поспелова Т.А. (2021). Сопровождение разработки нефтяных месторождений с использованием моделей CRM. Тюмень: ИПЦ «Экспресс», 300 с. https://doi.org/10.54744/TNSC.2021.53.50.001
6. Степанов С.В., Поспелова Т.А. (2019). Новая концепция математического моделирования для принятия решений по разработке месторождений. Нефтяное хозяйство, 4, с. 50–53. https://doi.org/10.24887/0028-2448-2019-4-50-53
7. Хатмуллин И.Ф., Андрианова А.М. и Маргарит А.С. (2018). Полуаналитические модели расчета интерференции скважин на базе класса моделей CRM. Нефтяное хозяйство, 12, с. 38–41. https://doi.org/10.24887/0028-2448-2018-12-38-41
8. Azadeh Mamghaderi, Peyman Pourafshary (2013). Water flooding performance prediction in layered reservoirs using improved capacitance-resistive model. Journal of Petroleum Science and Engineering, 108, pp. 107–117. http://dx.doi.org/10.1016/j.petrol.2013.06.006
9. Holanda R.W., Gildin E., Jensen J.L., Lake L.W., Kabir C.S. (2018). A State-of-the-Art Literature Review on Capacitance Resistance Models for Reservoir Characterization and Performance Forecasting. Energies, 11, 3368. https://doi.org/10.3390/en11123368
10. Lasdon L., Shirzadi S. and Ziegel E. (2017). Implementing CRM models for improved oil recovery in large oil fields. Optimization and Engineering, 18, pp. 87–103. https://doi.org/10.1007/s11081-017-9351-8
11. Olenchikov D., Posvyanskii D. (2019). Application of CRM-Like Models for Express Forecasting and Optimizing Field Development. SPE-196893-MS. SPE Russian Petroleum Technology Conference. Moscow, Russia.
12. Sayarpour M. (2008). Development and Application of Capacitance-Resistive Models to Water/CO2 Floods. Dissertation by Ph.D. Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy, p. 236. https:// doi.org/10.13140/RG.2.1.1798.3847
13. Sayarpour M., Kabir C.S., Lake L.W. (2008). Field Applications of Capacitance Resistive Models in Waterfloods. SPE Annual Technical Conference and Exhibition. https://doi.org/10.2118/114983-MS
14. Sayarpour M., Kabir C.S., Sepehrnoori K. and Lake L.W. (2010). Probabilistic History Matching With the Capacitance-Resistance Model in Waterfloods: A Precursor to Numerical Modeling. SPE Improved Oil Recovery Symposium, Tulsa, Oklahoma, USA, April. https://doi.org/10.2118/129604-MS
15. Sayarpour M., Zuluaga E., Kabir C.S., Lake L.W. (2009). The use of capacitance–resistance models for rapid estimation of waterflood performance and optimization. Journal of Petroleum Science and Engineering, 69(3–4), pp. 227–238. https://doi.org/10.1016/j.petrol.2009.09.006
16. Seng Wang, Zhen Zhang, Zhang Wen, Qihong Feng, Jingshi Wang, Zhengwu Tao, Zhen Wang, Xing Zhao (2023). Inferring the interwell connectivity of multilayer waterflooded reservoirs accounting for incomplete injection/production profiles. Geoenergy Science and Engineering, 227, 211897. https://doi.org/10.1016/j.geoen.2023.211897
17. Yousefi S.H., Rashidi F., Sharifi M. et al. (2019). Prediction of Immiscible Gas Flooding Performance: a Modified Capacitance–Resistance Model and Sensitivity Analysis. Pet. Sci., 16, pp. 1086–1104. https://doi.org/10.1007/s12182-019-0342-6
Об авторах
А. А. ГлушаковРоссия
Алексей Александрович Глушаков – младший научный сотрудник
119296, Москва, Ленинский проспект, д. 65, корп. 1
А. И. Архипов
Россия
Алексей Игоревич Архипов – кандидат техн. наук, старший научный сотрудник
119296, Москва, Ленинский проспект, д. 65
И. В. Афанаскин
Россия
Иван Владимирович Афанаскин – кандидат техн. наук, независимый исследователь, член Евразийского Союза экспертов по недропользованию (ЕСО ЭН)
117218, Москва, Нахимовский просп., д. 36, к. 1
Рецензия
Для цитирования:
Глушаков А.А., Архипов А.И., Афанаскин И.В. Модель взаимодействия скважин при заводнении слоисто-неоднородного нефтяного пласта в рамках концепции CRM-моделирования. Георесурсы. 2024;26(3):162-174. https://doi.org/10.18599/grs.2024.3.17
For citation:
Glushakov A.A., Arhipov A.I., Aafanaskin I.V. Model of Well Interference During Waterflooding of a Layered Heterogeneous Oil Reservoir within the Framework of the CRM Modeling Concept. Georesursy = Georesources. 2024;26(3):162-174. (In Russ.) https://doi.org/10.18599/grs.2024.3.17















.png)


