Перейти к:
Оценка пространственного распределения петрофизических свойств осадочных толщ многомерными сплайнами
https://doi.org/10.18599/grs.2024.3.18
Аннотация
В работе рассмотрена возможность применения многомерных аппроксимирующих и регрессионных сплайнов как с учетом пространственно привязанных данных прямых наблюдений, так и с использованием каротажных кривых, статистически связанных с моделируемыми переменными для оценки пространственной изменчивости свойств в осадочных толщах. За счет использования косвенных данных удается существенно снизить погрешность прогноза. Прогноз может строиться как для отдельных скважин, так и для межскважинного пространства, что позволяет создавать геологические разрезы прогнозируемых свойств и 3D-модели их распределения. Для доказательства эффективности рассматриваемого подхода проведены численные эксперименты на данных из стратиграфического диапазона георгиевской и васюганской свит Казанского месторождения на юго-востоке Западной Сибири. Сравнение полученного прогноза с реальными, неизвестными при его выполнении, значениями моделируемой переменной показало высокое качество модели с коэффициентами детерминации до 0,9.
Ключевые слова
Для цитирования:
Лапковский В.В., Конторович В.А., Канакова К.И., Пономарева С.Е., Лунёв Б.В. Оценка пространственного распределения петрофизических свойств осадочных толщ многомерными сплайнами. Георесурсы. 2024;26(3):175-183. https://doi.org/10.18599/grs.2024.3.18
For citation:
Lapkovsky V.V., Kontorovich V.A., Kanakova K.I., Ponomareva S.E., Lunev B.V. Prediction of the Spatial Distribution of Petrophysical Properties of Sediment Formations Using Multidimensional Splines. Georesursy = Georesources. 2024;26(3):175-183. (In Russ.) https://doi.org/10.18599/grs.2024.3.18
Введение
Петрофизические свойства осадочных пород определяются, как правило, для отдельных скважин, и только точечно, где поднят керн. Основными характеристиками, описывающими эти свойства, являются пористость, проницаемость, плотность породы. Прямых измерений может быть недостаточно для создания качественных пространственных моделей распределения свойств осадочных толщ. В таком случае приходится привлекать косвенную информацию, получаемую с помощью каротажа или в результате интерпретации сейсмических данных. Использование косвенных данных возможно, если удается выявить зависимости моделируемого параметра от других измеренных переменных. Если для примера рассмотреть определение пористости по данным каротажа, то для решения этой задачи известен ряд подходов. В классической работе (Головацкая и др., 1984) рассмотрены возможности оценки пористости по данным плотностного гамма-гамма- (ГГК-П), нейтронного (НК) и акустического (DTp) каротажа, а также совместное использование ГГК-П и НК. В методических рекомендациях по подсчету геологических запасов (Методические рекомендации…, 2003) приведены также зависимости для вычисления пористости по данным электрического и электромагнитного каротажа и метода, использующего эффект ядерно-магнитного резонанса. Известно большое количество работ, в которых пористость определяется на основе многомерных статистических зависимостей или с использованием обучаемых нейронных сетей. В некоторых работах сеть настолько близко воспроизводит данные реальных измерений, что коэффициент детерминации между прогнозными и измеренными величинами достигает 0,9999 (Wood, 2020). Подобный результат, скорее всего, свидетельствует о переобученности сети, он не может служить мерой качества прогноза. Примером успешного корректного применения рекуррентной нейронной сети к прогнозированию пористости по комплексу из 10 видов каротажа служит, например, работа китайских ученых (Yu еt al., 2023). Во многих публикациях прогноз пористости осуществляется благодаря интерпретации сейсмических данных (Безходарнов и др., 2021; Liu et al., 2023). Наиболее часто пористость и другие фильтрационно-емкостные свойства оцениваются по результатам акустической инверсии (Boer et al., 1999; Шаповалов и др., 2023; Su еt al., 2023).
Для объединения в общую модель различных оценок, полученных по разным данным и имеющих разные погрешности, могут использоваться несколько подходов. Может быть построена многомерная регрессионная зависимость, в которой данные с разными погрешностями будут учитываться с разными весами. Однако в таком случае возникает вопрос: как определить эти веса, которые, очевидно, должны зависеть от погрешности оценок. Другой подход к объединению разнородной информации основан на использовании кокригинга. Кокригинг применялся при создании моделей пористости, учитывающих как скважинные данные, так и результаты сейсмической инверсии (Boer et al., 1999; Doyen, 2007). Один из эффективных численных методов кокригинга – это колакационный кокригинг (Демьянов, Савельева, 2010), который не требует вычисления кросс-ковариаций и учитывает данные по дополнительным переменным только в ближайших окрестностях точек оценивания. Этот вид кригинга предполагает линейную связь ковариации основной переменной с кросс-ковариацией.
Целью настоящей работы является создание пространственной модели петрофизичеких параметров на основе применения многомерных сплайнов с использованием как прямых наблюдений, так и косвенной информации. Последовательно решались задачи прогноза параметров вдоль траекторий скважин и в межскважинном пространстве. В отличие от колакационного кокригинга, многомерные сплайны не накладывают ограничения на вид связи основной и дополнительных переменных. Кроме того, хотя теоретически, кокригинг позволяет одновременно учитывать несколько дополнительных переменных, на практике из-за сложности метода используется только одна такая переменная. Сплайны легко позволяют учитывать любое разумное число дополнительных переменных, в настоящей работе таких переменных было две – акустический каротаж и нейтронный каротаж. В работе не ставилась задача сравнения качества получаемых оценок с теми, которые возникают при кокригинге, однако построенная модель имеет довольно хорошее совпадение с контрольными значениями в скважинах, коэффициент детерминации с ними в некоторых скважинах достигал 0,9.
Метод
Для создания модели пространственного распределения петрофизических свойств нами использован один вид сплайнов, выраженный через радиально-базисные функции – RBF-сплайны (Роженко, 2005). Модели строились в пространствах старших размерностей, а в них достаточно просто работать именно с этим видом сплайнов. В трехмерном евклидовом пространстве вертикальная координата, замеряющая глубину, была заменена на связанную с ней стратиграфическую переменную, которая имеет одинаковые значения для всех стратиграфически эквивалентных точек. В геологическом моделировании так обычно поступают, чтобы пространственные распределения вычисляемых величин зависели от топологии слоистой толщи. Между заданными границами стратиграфическая переменная непрерывна. Если требуется создать модель для толщ, имеющих несогласия или прилегания, то могут применяться специальные преобразования. Процесс создания стратиграфической модели в том числе с несколькими несогласиями был описан нами ранее (Лапковский и др., 2023).
Далее для зависимой переменной (в настоящей работе это прореженные значения ГГК-П) построена аппроксимация с помощью многомерных сплайнов. При этом сами радиальные базисные функции конструируются с использованием косвенных данных. Если ставить задачу построить модель для параметра z (это может быть пористость или плотность пород) и если z статистически связана с другими параметрами, например со значениями нейтронного или акустического каротажа, то эти виды каротажа могут использоваться для конструирования радиальных базисных функций. Это отчасти аналогично методу кокригинга при пространственном моделировании. Смысл такой постановки возникает, если значения z известны для малого количества точек, а статистически связанные с ней переменные охарактеризованы существенно бóльшим числом данных.
Модель строилась на основе аппроксимирующих и регрессионных сплайнов. Регрессионные сплайны используются в случае очень большого числа наблюдений (десятки тысяч значений и более). Регрессионная модель предполагает, что некоторая переменная представляется как линейная комбинация базисных функций. Коэффициенты в уравнении при этих базисных функциях определяются методом наименьших квадратов, с помощью которого минимизируется выражение
![]() , (1)
, (1)
где zi – наблюденные данные, δ(x) – уравнение регрессии.
Обычно полагается, что все измерения равнозначны и имеют одинаковый вес. В случае, когда измерения учитываются с разными весами, вместо (1) минимизируется выражение
![]() , (2)
, (2)
здесь wi – вес, который соответствует i-му наблюдению.
В настоящей работе использована сплайн-регрессия (Роженко, 2005; 2018), особенность которого состоит в том, что количество опорных узлов сплайна многократно меньше числа точек, в которых известны аппроксимируемые значения. В общем случае опорные узлы могут даже не являться подмножеством точек с исходными данными. Применяемый сплайн имеет вид
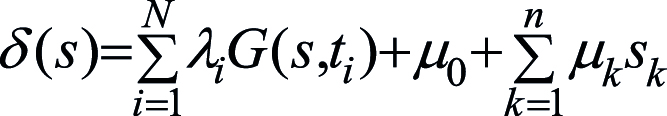 , (3)
, (3)
где G(s,t) = g(|s – t|) – радиальная функция, s = (s1,…,sn), ti = (ti,1,…,ti,n), i = 1,…,N, – опорные узлы сплайна в n-мерном пространстве ![]() ,
,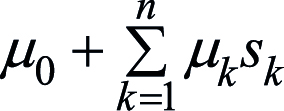 – линейная компонента сплайна,
– линейная компонента сплайна,
λi – коэффициенты при радиальных функциях. Коэффициенты λi в случае сплайн-регрессии находятся методом наименьших квадратов. Сплайн-регрессия отличается от обычной многомерной регрессии тем, что в ней используются радиальные функции, связанные с набором опорных узлов, в то время как в обычной многомерной регрессии могут использоваться любые функции.
Вид сплайна зависит от выбора типа радиальных функций. В приведенных ниже примерах применялись наиболее простые из возможных – псевдолинейные сплайны (Роженко, 2005).
Подтверждение эффективности модели
Приведем полученные нами на полуискусственном примере результаты, которые показывают, насколько эффективно предлагаемое решение прогноза петрофизических характеристик.
Суть проведенного численного эксперимента состоит в следующем.
- Рассмотрен один из методов каротажа, а именно ГГК-П, и принято, что это и есть интересующий параметр, для которого нужно построить модель его пространственного распределения.
- Удалены почти все значения ГГК-П из массива исходной информации. В данном эксперименте каротаж ГГК-П – это аналог параметра, значения которого можно установить, только подняв керн. Соответственно, только эти части скважин и с интервалом 10 м между образцами использовались при вычислениях. Таким образом, при создании сплайна, который служит для моделирования пространственного распространения прогноза значений ГГК-П, в качестве прямых измерений использовано менее 1% имеющихся данных (исходный каротаж ГГК-П записан с шагом 0,1 м, а также учтены данные не всех скважин).
- Остальные виды каротажа, для которых существуют статистически значимые связи с ГГК-П, использовались в полном объеме. В качестве таких методов взяты акустический каротаж (DTp) и нейтронный каротаж по тепловым нейтронам (NKT1).
- Далее строили сплайн и сравнивали его значения с известными во всех точках измерениями ГГК-П во всех скважинах, включая контрольные, в которых «условный керн» не отбирался. Результат сравнения является метрикой эффективности решения.
Такой численный эксперимент хорош тем, что дает уверенность в качестве данных и их взаимной увязке в пространстве. Если брать реальные каротажные измерения и результаты аналитических анализов керна, то неизбежно возникают сомнения в качестве привязки керна и каротажа по стволу скважины. Кроме того, довольно трудно оценить собственные ошибки аналитических определений пористости. Эти ошибки зависят от размеров анализируемых образцов и вызываются так называемым масштабным эффектом (Гурбатова, Михайлов, 2011; Lie, 2019; Хасанов, Лоншаков, 2020). Кроме того, разные методики (по воде, по керосину, по гелию) могут приводить к существенным расхождениям результатов, иногда достигающим десятков процентов абсолютных значений пористости (Гильманов, 2020). Тогда плохие результаты прогноза могут быть обусловлены как плохо работающим алгоритмом построения модели, так и ошибками совмещения керна и каротажа. В нашем случае таких сомнений нет, более того, для начала брались только скважины одного эксплуатационного куста, где каротаж увязан по глубине, получен на одинаковых приборах в близких условиях и, если использовалась обработка кривых, то она была одинакова для всех стволов.
Модель построена для отложений георгиевской и васюганской свит в 24 стволах одного эксплуатационного куста Казанской площади. Из рис. 1 видно, что между значениями плотностного каротажа, DTp и NKT1 существует зависимость. На рисунке в левых треках скважин показаны кривые ГГК-П. Правые треки содержат по две кривые DTp и NKT1. Значения DTp показаны цветовой заливкой на треке с акустическим каротажем. Очевидна согласованность изменения форм рассматриваемых трех видов каротажа.
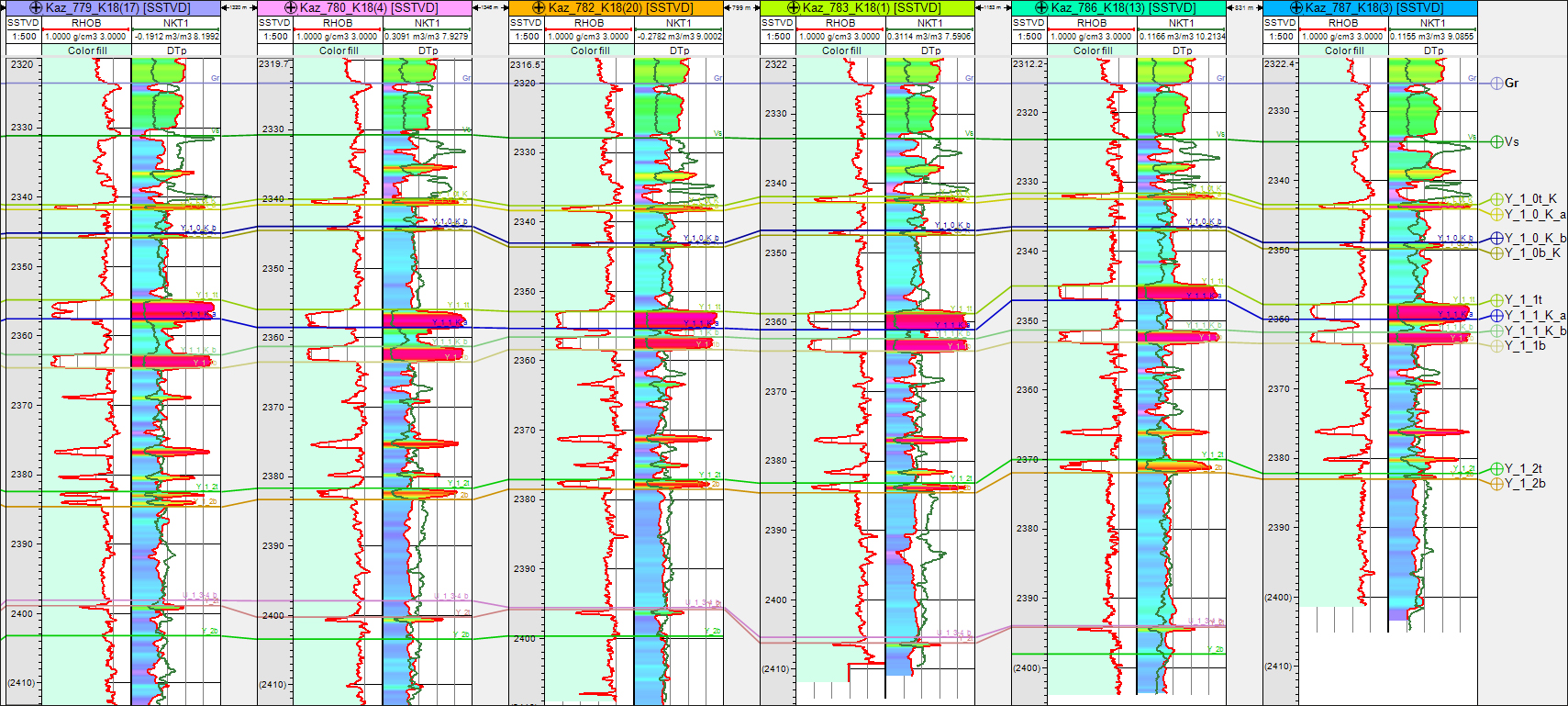
Рис. 1. Каротаж разреза георгиевской и васюганской свит
в нескольких скважинах Казанской площади
Как отмечено выше, на базе кривой ГГК-П построены аналоги лабораторных измерений плотности пород с отбором керна через 10 м. Полученная таким образом переменная названа MODEL_DENS, ее вид имеет мало общего с исходным ГГК-П (рис. 2). Однако для 113 сгенерированных измерений отчетливо прослеживается статистическая связь со значениями DTp и NKT1 (рис. 3).
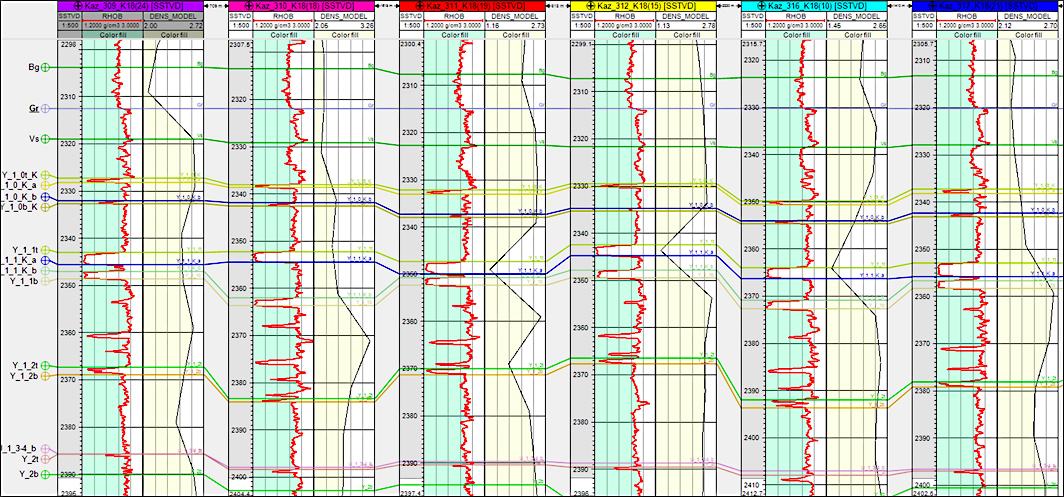
Рис. 2. Каротаж ГГК-П и созданные данные как бы аналитических определений (MODEL_DENS)
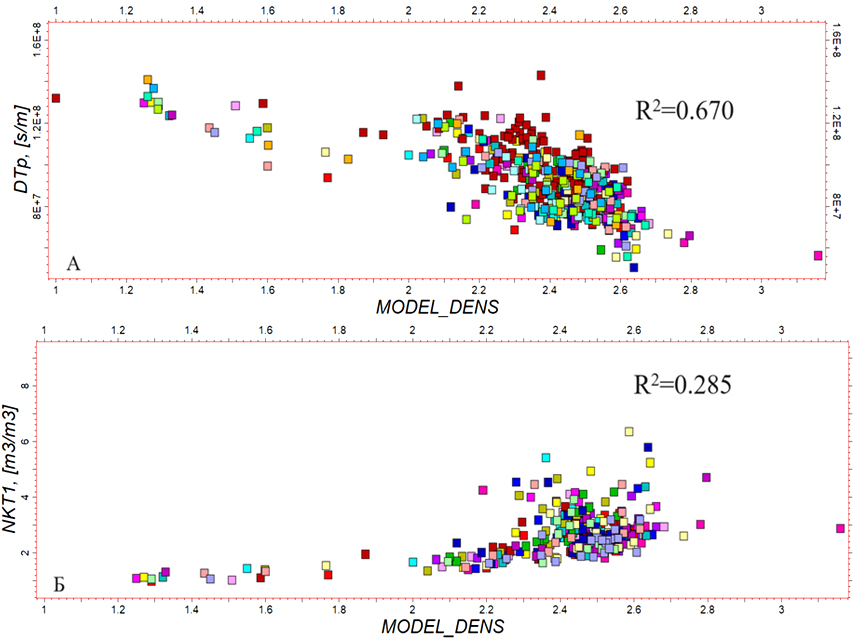
Рис. 3. Зависимость MODEL_DENS и значений каротажа: А – DTp, Б – NKT1.
Разные цвета точек на диаграмме соответствуют различным скважинам
Набор из 152 точек, для которых известны значения всех трех видов каротажа (MODEL_DENS, NKT1 и DTp), позволяет решить уравнение линейной регрессии и спрогнозировать величину MODEL_DENS. Коэффициент детерминации для этой регрессионной зависимости составил 0,677. По шкале Четтдока такой уровень говорит о высокой корреляционной связи. На рис. 4 представлен кросс-плот, показывающий измеренные и найденные из решения уравнения регрессии значения MODEL_DENS.
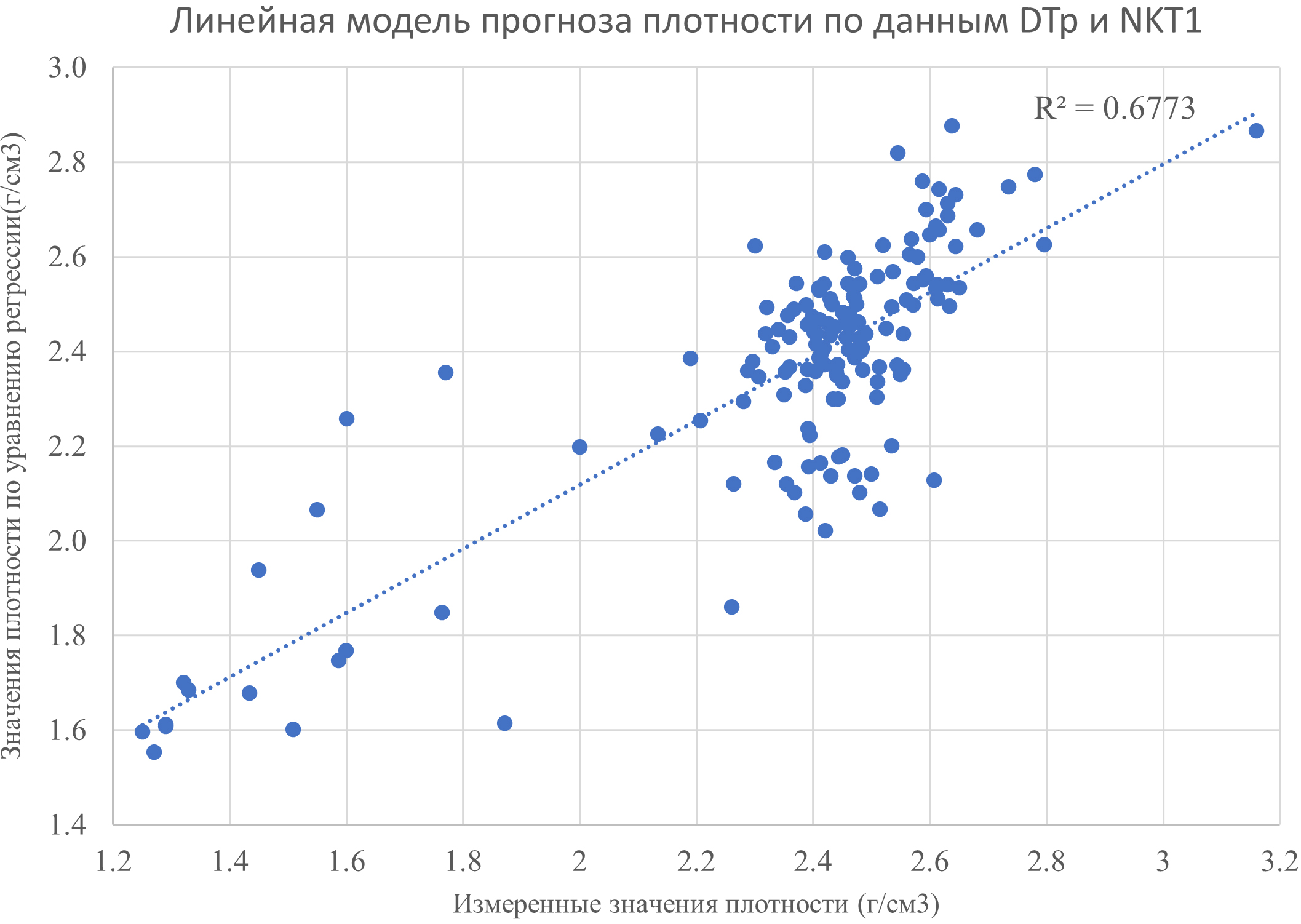
Рис. 4. Сравнение прогнозных (по уравнению двумерной регрессии)
и сгенерированных значений MODEL_DENS
Сам прогноз на фоне истинных значений ГГК-П графически представлен на рис. 5. Как видно из рисунка, полученный результат оказался неудовлетворительным. Имеются систематические отклонения в сторону завышения прогнозных значений от истинных.
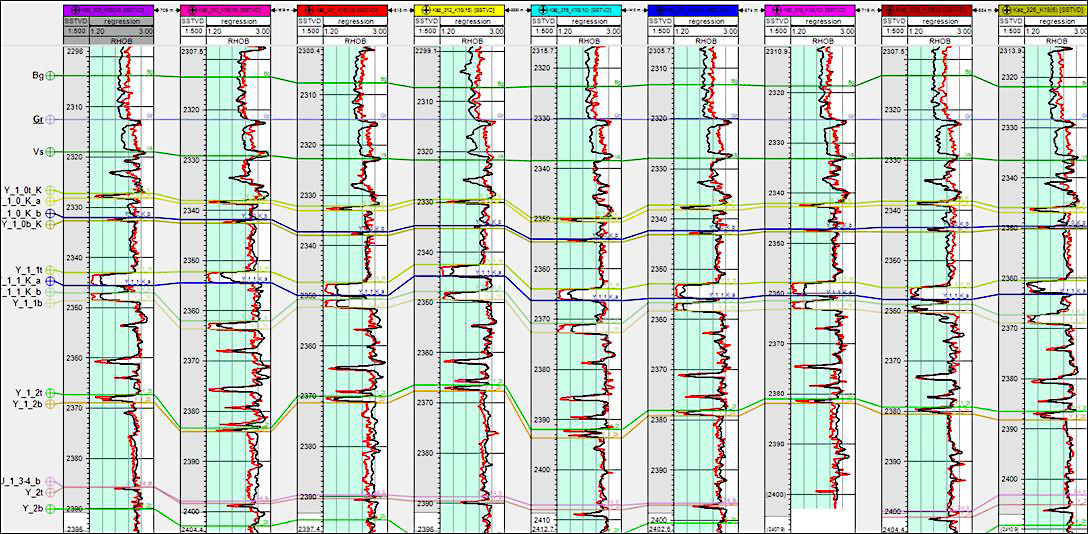
Рис. 5. Истинные значения моделируемого параметра MODEL_DENS
(кривая ГГК-П, красная кривая) и прогнозные значения
(на основе пересчета из DTp и NKT1, черная кривая)
Рис. 6 построен уже с помощью сплайновой модели. Видно, что прогноз, сделанный с помощью многомерных сплайнов, оказался более точным.
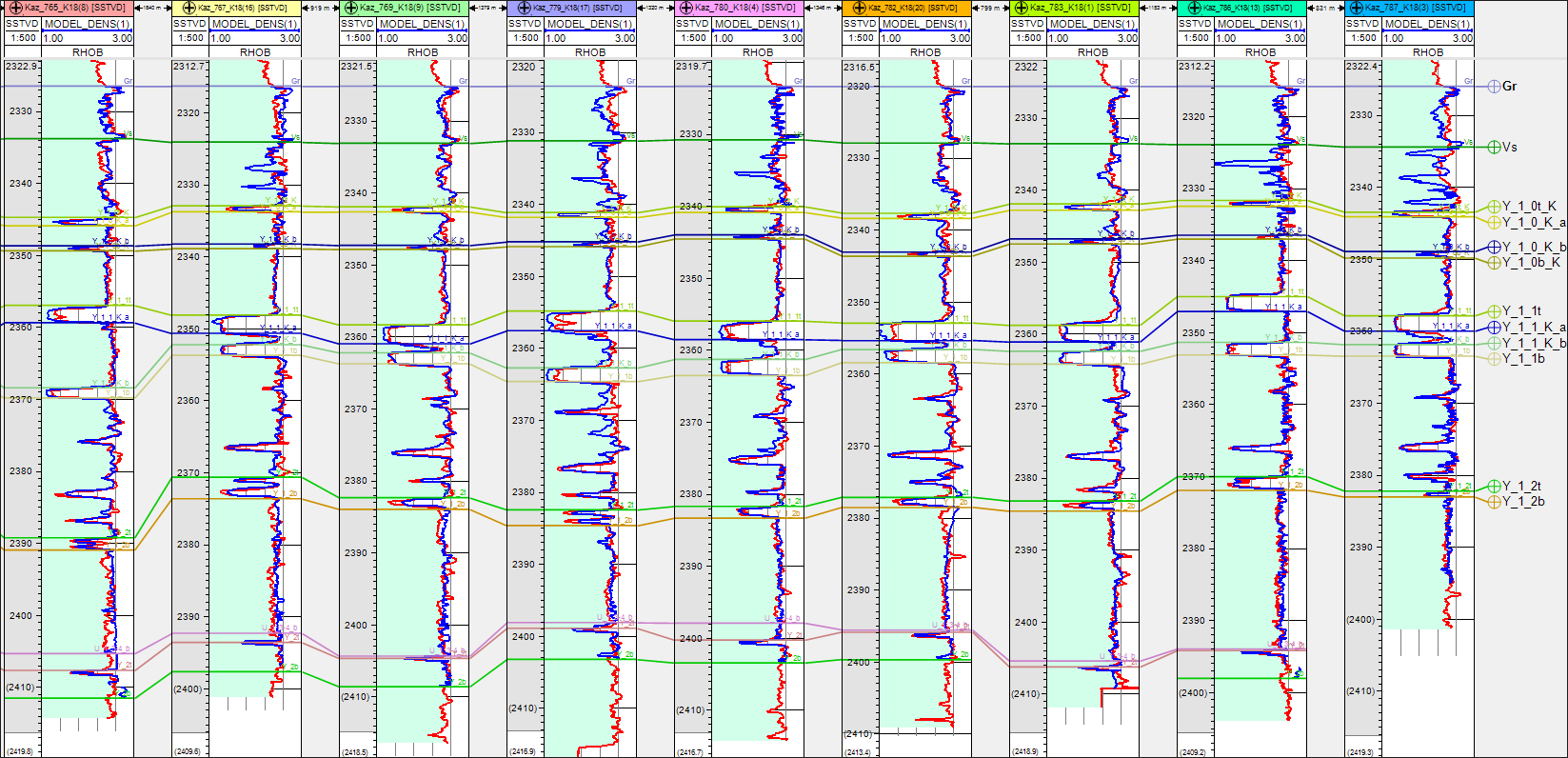
Рис. 6. Сравнение реальных (красная кривая) и прогнозных (синяя кривая) значений,
полученных на основе сплайн-аппроксимации
Таким образом, в этом случае имеем более точное сходство реальных и прогнозных значений. Особый интерес представляет соответствие прогнозных и истинных значений в тех скважинах, в которых не получен «керн» (в проведенном эксперименте в этих скважинах не было задано ни одного значения MODEL_DENS). Это четыре крайние правые скважины на рис. 6, где результат прогноза визуально хорошо согласуется с реальными значениями. Для каждой из этих четырех скважин были вычислены парные коэффициенты корреляции между истинными значениями и результатом прогноза на основе сплайн-аппроксимации. Полученные значения составили (по порядку скважин слева направо): 0,93; 0,93; 0,84; 0,82. Коэффициент детерминации меняется от 0,67 до 0,87, что значительно лучше, чем было спрогнозировано на основе двумерной линейной регрессии. Для скважин, участвующих в создании модели сплайна, коэффициенты корреляции оказались чуть выше и достигали значения 0,95.
Отметим одно важное достоинство используемого метода – возможность прогноза значений параметров в межскважинном пространстве.
Сплайн является непрерывной функцией, поэтому он может быть вычислен для любой точки пространства. Это позволяет строить трехмерные модели распределения свойств и любые двумерные срезы (горизонтальные, вертикальные, наклонные, сложной геометрии). На рис. 7 представлены разрезы для объемной модели, которая построена уже по всем скважинам месторождения (но опять же только для одной точки прямых данных с каждых 10 м разреза).
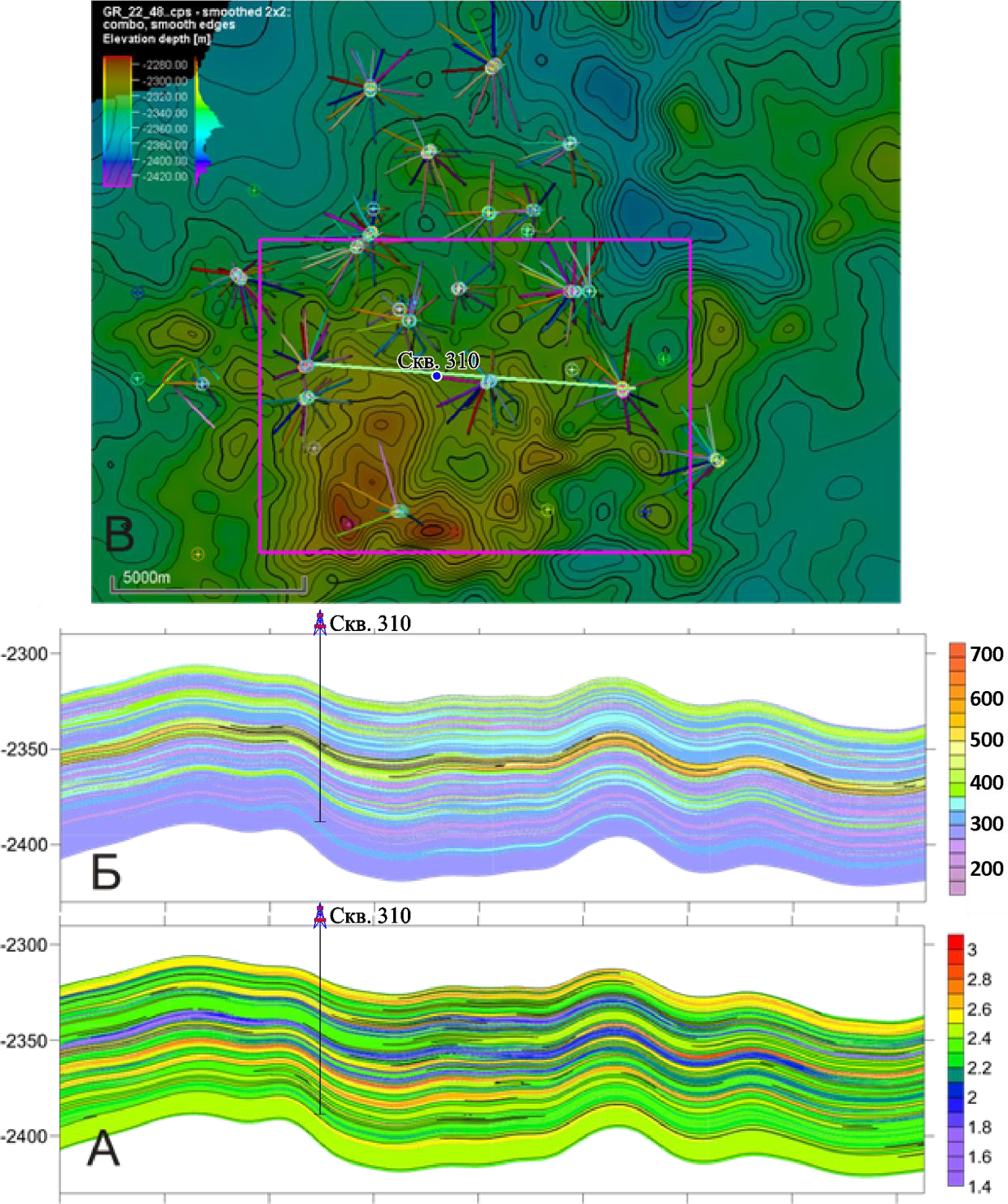
Рис. 7 Разрезы георгиевской и васюганской свит,
извлеченные из объемной модели Казанского месторождения:
А – разрез смоделированных значений плотности пород – цветовая шкала в г/см³;
Б – разрез DTp – цветовая шкала в м/мкс;
В – структурная карта кровли георгиевской свиты с положением разрезов
(линия зеленого цвета)
Срезы разной ориентации построенной трехмерной модели показаны на рис. 8. Область, для которой вычислена модель, выделена розовым прямоугольником на рис. 7.
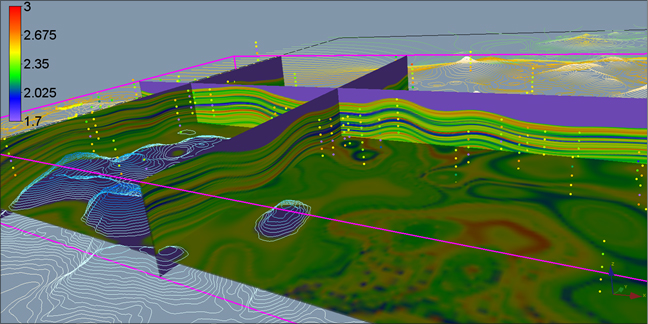
Рис. 8. Срезы трехмерного распределения спрогнозированной плотности пород (шкала – г/см³).
Цветные точки – прямые данные, использованные для создания модели.
Изолинии принадлежат подстилающей поверхности – подошве пласта Ю₂¹
Установлена высокая сходимость модельных значений плотности со значениями каротажа ГГК-П. Разрез плотности на качественном уровне иллюстрирует литологические особенности среды. Так, протяженный слой, характеризующийся наиболее пониженной плотностью (уровень, колеблющийся вблизи отметки –2350 м на разрезах), ассоциируется с угольным пластом У₁¹. Стоит отметить высокую сходимость мощностей на модели и в скважинах. Геологичность модели также подчеркивается характером распределения пласта по площади: он присутствует повсеместно, мощность меняется в пределах от 6 до 12 м. Кроме того, в разрезе четко прослеживается серия менее мощных слоев с пониженной плотностью, они вполне соответствуют угольным пластам, вскрытым в межугольной и надугольной пачках васюганской свиты, а слои с наиболее высокими значениями плотности, имеющие локальное распространение по латерали, могут быть сопоставлены с прослоями карбонатизированных песчаников и ракушняков.
Отдельно остановимся на скв. № 310, в которой угольный пласт У₁¹ имеет аномальное строение. Мощность угольной пачки здесь сильно увеличена и пласт разделен на две части толщей песчано-алевритового состава. Это связано с тем, что отложения кровли межугольной пачки на большей части изучаемой территории формировались в условиях илистой заболоченной равнины, однако выявлен ряд линейных зон, к которым приурочены небольшие по мощности песчаные тела аллювиального генезиса, разделяющие пласт У₁¹. На срезе модели в районе скв. № 310 на уровне –2360 м можно наблюдать локальное увеличение значения плотности внутри пласта, соответствующего У₁¹. Для этой же области на разрезах 7А, Б четко видно двухчленное строение угольной пачки, где от основного пласта влево и чуть вниз уходит клин пород с высокими значениями DTp и низкой плотностью.
Для всех скважин месторождения расчетные величины плотности оказались достаточно близкими к измерениям ГГП-К, из которых были отобраны только 274 значения прямых наблюдений.
Реализация
Для построения петрофизических моделей на основе многомерной сплайн-аппроксимации реализовано два варианта. Один из них включен в состав комплекса интерпретации сейсмических и скважинных данных W-SEIS (Канаков и др., 2022), другой является плагином для Petrel Schlumberger. Оба варианта позволяют прогнозировать петрофизические параметры в скважинах на основе имеющихся данных каротажа, строить разрезы по любым линиям, создавать трехмерные объекты, вычислять значения параметров на заданных поверхностях (на границах тел), а также составлять карты средних значений (арифметических, геометрических, гармонических) для тел между двумя заданными структурными поверхностями.
Результаты исследования были представлены на Всероссийской научной конференции, посвященной 90-летию со дня рождения академика РАН А.Э. Конторовича «Фундаментальные, глобальные и региональные проблемы геологии нефти и газа» (Лапковский и др., 2024).
Заключение
Представленные результаты показали достоинства моделирования пространственного распределения петрофизических параметров на основе применения многомерных сплайнов. При этом одновременно достигается весьма качественное восстановление искомых петрофизических переменных в скважинах (при условии, что их значения зависят от других каротажных данных, зарегистрированных в большинстве скважин) и адекватное поведение параметров модели в межскважинном пространстве. Прогноз на основе сплайнов дает меньшие погрешности по сравнению с использованием многомерных линейных регрессий. Преимущество сплайнов основывается на том, что сплайны учитывают пространственное положение скважин и всех точек измерения, по ним строится согласованная модель. При использовании уравнений регрессии имеют большое значение статистические связи между переменными, но при этом пространственное положение данных не учитывается.
Отметим, что созданная технология легко позволяет дополнить пространство переменных сейсмическими атрибутами, что может быть полезно при прогнозировании петрофизических параметров в межскважинном пространстве, например, с привлечением результатов сейсмической инверсии.
Финансирование/Благодарности
Работа выполнена в рамках научной темы FWZZ-2022-0009 «Цифровые геолого-геофизические модели и оценка перспектив нефтегазоносности осадочных бассейнов Арктической зоны Сибири и республики Саха (Якутия); усовершенствование геолого-геофизических методов исследований» Государственной программы ФНИ.
Авторы выражают благодарность рецензентам за ценные замечания и предложения, которые способствовали повышению уровня работы.
Список литературы
1. Безходарнов В.В., Чичинина Т.И., Коровин М.О., Трушкин В.В. (2021). Прогнозирование фильтрационно-ёмкостных свойств пород по данным сейсморазведки на основе многомерного вероятностного анализа. Российская нефтегазовая техническая конференция SPE, SPE-206595-RU. https://doi.org/10.2118/206595-MS
2. Гильманов Я.И. (2020). Опыт ООО «ТННЦ» в определении пористости образцов керна. Нефтепромысловое дело, (9), с. 35–41. https:// doi.org/10.30713/0207-2351-2020-9(621)-35-41
3. Головацкая И.В., Гулин Ю.А., Еникеева Ф.Х., Велижанин В.А., Журавлев Б.К., Козяр В.Ф., Ручкин А.В., Резванов Р.А. (1984). Определение емкостных свойств и литологии пород в разрезах нефтегазовых скважин по данным радиоактивного и акустического каротажа (наставление по интерпретации с комплектом палеток). Калинин, ВНИГИК, 111 с.
4. Гурбатова И.П., Михайлов Н.Н. (2011). Масштабные и анизотропные эффекты при экспериментальном определении физических свойств сложнопостроенных коллекторов. Каротажник, (7), с. 138–145.
5. Демьянов В.В., Савельева Е.А. (2010). Геостатистика: теория и практика. М.: Наука, 327 с.
6. Канаков М.С., Лапковский В.В., Конторович В.А., Канакова К.И., Шорохов Ю.С. (2022). Программный комплекс интерпретации сейсмических и скважинных данных W-SEIS. Геофизические технологии, (2), с. 77–91. https://doi.org/10.18303/2619-1563-2022-2-77
7. Лапковский В.В., Лунёв Б.В., Антипов М.П., Волож Ю.А., Писаренко Ю.А., Фомина В.В. (2023). Трехмерное моделирование солянокупольных структур по данным детального бурения в Прикаспии. Георесурсы, 25(4), c. 192–202. https://doi.org/10.18599/grs.2023.4.18
8. Лапковский В.В., Конторович В.А., Канакова К.И., Пономарева С.Е., Лунев Б.В. (2024) Фундаментальные, глобальные и региональные проблемы геологии нефти и газа: Материалы Всероссийской научной конференции, посвященной 90-летию со дня рождения академика РАН А.Э. Конторовича с. 129-132 https://dx.doi.org/10.53954/9785604990070_129
9. Методические рекомендации по подсчету геологических запасов нефти и газа объемным методом. (2003). Под ред. В.И. Петерсилье, В.И. Пороскуна, Г.Г. Яценко. М.: ВНИГНИ; Тверь: Тверьгеофизика. 267 с.
10. Роженко А.И. (2018). Сравнение радиальных базисных функций. Сибирский журнал вычислительной математики, 21(3), с. 273–292. https://doi.org/10.15372/SJNM20180304
11. Роженко А.И. (2005). Теория и алгоритмы вариационной сплайн-аппроксимации. Новосибирск: ИВМиМГ СО РАН, 244 с.
12. Хасанов Д.И., Лоншаков М.А. (2020). Исследование масштабного эффекта и понятия элементарного представительного объёма горных пород применительно к пористости. Георесурсы, 22(4), c. 55–69. https:// doi.org/10.18599/grs.2020.4.55-69
13. Шаповалов М.Ю., Хамитуллин И.М., Шакиров Р.Р., Филиппова К.Е., Брегида А.А. (2023). Использование сейсмической инверсии для прогноза коллектора в интервале прибрежно-континентальных отложений юрского комплекса. Георесурсы, 25(3), c. 49–56. https://doi.org/10.18599/grs.2023.3.7
14. Boer L.D.D., Doyen Ph.M., Rothenhofer H. (1999). 3-D seismic porosity modeling using a new form of cokriging. World Oil, 5(220) pp. 77–80.
15. Doyen P.M. (2007). Seismic Reservoir Characterization: An Earth Modelling Perspective. EAGE, 255 p. https://doi.org/10.3997/9789073781771
16. Lie K.-A. (2019). An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST). Cambridge: Cambridge University Press, 678 p. https:// doi.org/10.1017/9781108591416
17. Liu J., Zhao L., Xu M., Zhao X., You Y., Geng J. (2023). Porosity prediction from prestack seismic data via deep learning: incorporating a lowfrequency porosity model. Journal of Geophysics and Engineering, 20(5), pp. 1016–1029. https://doi.org/10.1093/jge/gxad063
18. Su Z., Cao J., Xiang T., Fu J., Shi S. (2023). Seismic prediction of porosity in tight reservoirs based on transformer. Frontiers in Earth Science, 11, 1137645. https://doi.org/10.3389/feart.2023.1137645
19. Wood D.A. (2020). Predicting porosity, permeability and water saturation applying an optimized nearest-neighbour, machine-learning and data-mining network of well-log data. Journal of Petroleum Science and Engineering, 184, 106587. https://doi.org/10.1016/j.petrol.2019.106587
20. Yu Z., Sun Y., Zhang J., Zhang Y., Liu Z. (2023). Gated recurrent unit neural network (GRU) based on quantile regression (QR) predicts reservoir parameters through well logging data. Frontiers in Earth Science, 11, 1087385. https://doi.org/10.3389/feart.2023.1087385
Об авторах
В. В. ЛапковскийРоссия
Владимир Валентинович Лапковский – доктор геол.-минерал. наук, заведующий лабораторией
630090, Новосибирск, пр. Ак. Коптюга, д. 3
В. А. Конторович
Россия
Владимир Алексеевич Конторович –доктор геол.-минерал. наук, член-корр. РАН, заведующий лабораторией
630090, Новосибирск, пр. Ак. Коптюга, д. 3
К. И. Канакова
Россия
Ксения Игоревна Канакова – младший научный сотрудник; младший научный сотрудник, ассистент
630090, Новосибирск, пр. Ак. Коптюга, д. 3
С. Е. Пономарева
Россия
Светлана Евгеньевна Пономарёва – ведущий программист
630090, Новосибирск, пр. Ак. Коптюга, д. 3
Б. В. Лунёв
Россия
Борис Валентинович Лунёв – кандидат физ.-мат. наук, старший научный сотрудник
630090, Новосибирск, пр. Ак. Коптюга, д. 3
Рецензия
Для цитирования:
Лапковский В.В., Конторович В.А., Канакова К.И., Пономарева С.Е., Лунёв Б.В. Оценка пространственного распределения петрофизических свойств осадочных толщ многомерными сплайнами. Георесурсы. 2024;26(3):175-183. https://doi.org/10.18599/grs.2024.3.18
For citation:
Lapkovsky V.V., Kontorovich V.A., Kanakova K.I., Ponomareva S.E., Lunev B.V. Prediction of the Spatial Distribution of Petrophysical Properties of Sediment Formations Using Multidimensional Splines. Georesursy = Georesources. 2024;26(3):175-183. (In Russ.) https://doi.org/10.18599/grs.2024.3.18















.png)


