Перейти к:
Прогнозирование вязкостно-температурной зависимости смеси нефтей по информации об их плотности, содержании парафина, смол, асфальтенов и фракционном составе
https://doi.org/10.18599/grs.2024.3.23
Аннотация
Предложен новый способ прогнозирования вязкостно-температурных характеристик смесей нефтей различных месторождений, непрерывно образующихся в процессе выполнения технологических операций при их сборе, транспорте и переработке в разветвленных трубопроводных системах. Основная идея заключается в определении корреляционной зависимости вязкости нефти от других ее физико-химических свойств, которые при смешении нефтей поддаются аддитивному расчету. Такими параметрами являются плотность, содержание высокомолекулярных соединений, их фракционный состав и т.п. По корреляционной зависимости можно оценить значение вязкости смеси после определения расчетным способом ее аддитивных физико-химических свойств. По известным характеристикам нефтей подобраны и проанализированы различные регрессии первого и второго рода с целью построения уравнений для определения вязкости при температурах 10 °С, 20 °С, 30 °С, 40 °С, 50 °С в зависимости от указанных аддитивных параметров. Предложен также способ определения вязкостно-температурной зависимости нефти на основе уравнения Рейнольдса – Филонова. Полученные погрешности определения вязкости являются допустимыми для выполнения предварительных прогнозных расчетов энергопотребления перекачки при планировании грузопотоков нефтей различных месторождений по разветвленной трубопроводной системе.
Для цитирования:
Валеев А.Р., Ташбулатов Р.Р., Чэнь Я., Каримов Р.М. Прогнозирование вязкостно-температурной зависимости смеси нефтей по информации об их плотности, содержании парафина, смол, асфальтенов и фракционном составе. Георесурсы. 2024;26(3):232-239. https://doi.org/10.18599/grs.2024.3.23
For citation:
Valeev A.R., Tashbulatov R.R., Chen Y., Karimov R.M. Prediction of the Viscosity-Temperature Dependence of a Mixture of Oils Based on Information about the Density, Content of Paraffin, Resins, Asphaltenes and Fractional Composition. Georesursy = Georesources. 2024;26(3):232-239. (In Russ.) https://doi.org/10.18599/grs.2024.3.23
1. Введение
Современные крупные нефтепроводные системы таких стран, как Россия, США и Китай, представляют собой большие разветвленные сети. Планирование и управление технологическими операциями, а также выбор необходимых режимов перекачки нефти на отдельных частях системы является сложной и важной задачей, так как напрямую влияет на энергопотребление, следовательно, и на экономические показатели эффективности трубопроводного транспорта нефти. Затраты энергии компенсируют потери напора на трение при движении нефти по трубопроводам, величина которых, в свою очередь, определяется вязкостью перекачиваемой нефти (Chen et al., 2023).
Значения вязкости различных нефтей могут сильно отличаться друг от друга. Например, различие показателей вязкости маловязкой и высоковязкой нефтей, поступаемых в систему магистральных трубопроводов России, может составлять до 100 раз (Ташбулатов, 2019), следовательно, и затраты на перекачку таких нефтей при одних и тех же условиях могут отличаться существенным образом (Langbauer et al., 2021). Поэтому прогнозирование вязкости образующихся в процессе выполнения технологических операций смесей нефтей из различных месторождений является важной задачей при проектировании новых трубопроводов и расчете технологических режимов перекачки.
При перекачке по трубопроводу нефти с неизменными свойствами задача прогнозирования энергопотребления не является сложной. Однако при транспортировке нефтей из различных месторождений с отличающимися свойствами в отдельных частях трубопроводной системы перекачиваются технологические смеси с различным содержанием исходных смешиваемых нефтей, а соответственно, с различной вязкостью. С учетом регулярного изменения режимов перекачки на отдельных участках нефтепроводов нефть смешивается в разных порциях (Аралов и др., 2017). Таким образом, на каждом участке нефтепроводной системы могут меняться не только технологические параметры перекачки, но и свойства нефти. Для рационального прогнозирования и управления режимами работы трубопровода, а также для более точной оценки энергопотребления необходимо прогнозировать вязкость перекачиваемой технологической смеси в любой момент времени с учетом поступаемых в систему объемов нефти. Однако следует отметить, что вязкость смеси нефтей не поддается аддитивному расчету.
В простейшем случае вязкость можно оценить с помощью уравнения Аррениуса (Аралов и др., 2017):
![]() , (1)
, (1)
где vmix – коэффициент кинематической или динамической вязкости смеси; v1, v2 – коэффициенты кинематической или динамической вязкости исходных смешиваемых нефтей; x1, x2 – соотношения исходных смешиваемых нефтей.
Для описания изменения вязкости при смешении также часто используют следующие уравнения (Ташбулатов, 2019):
– уравнение Кендаля и Монрое
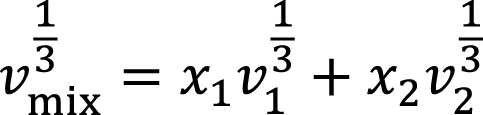 (2)
(2)
– уравнение Керна (Бингама, Здановского)
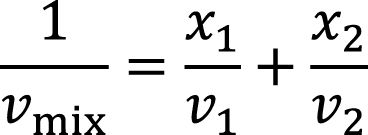 (3)
(3)
– уравнение Вальтера
![]() (4)
(4)
В табл. 1 представлены математические модели для определения вязкости бинарных нефтяных смесей, описанные в работах (Ташбулатов, 2019; Закиров, 2016; Al-Maamari et al., 2015; Han et al., 2007; Khan et al., 1984; Miadonye et al., 2000; Miadonye et al., 1995; Miadonye et al., 1994; Puttagunta et al., 1993; Zhang et al., 2007).
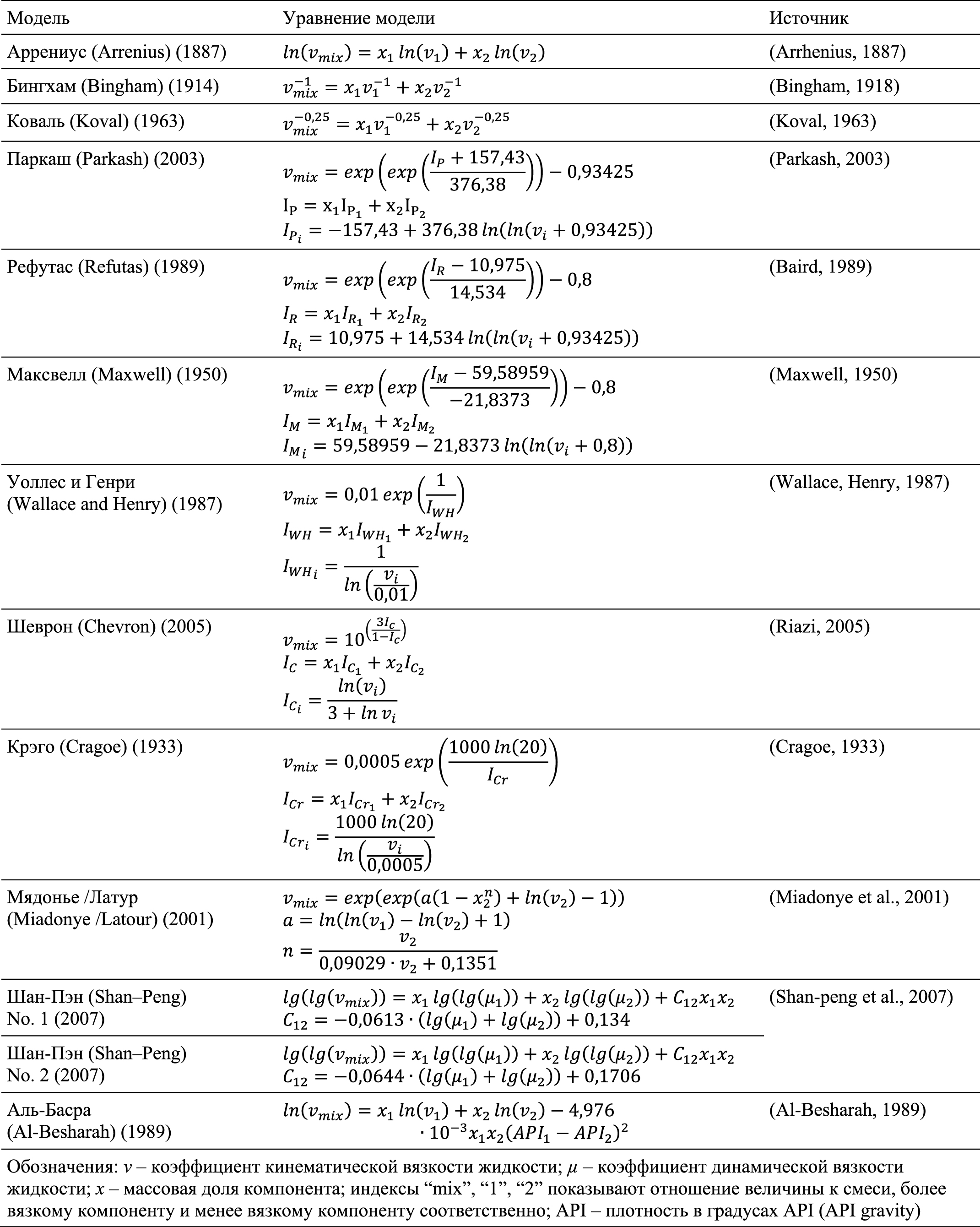
Табл. 1. Математические модели для определения вязкости бинарных нефтяных смесей
Перечисленные математические модели для определения вязкости нефтяной бинарной смеси имеют свои достоинства и недостатки. В частности, поскольку вязкость смеси зависит от физико-химических свойств исходных смешиваемых компонентов, то и упрощенные подходы, использующие только значение вязкости и доли смешиваемых исходных нефтей в смеси, будут заведомо иметь ограниченную точность. Эти модели не учитывают возможное проявление неньютоновского характера течения смешиваемых компонентов, а также имеют низкую точность при прогнозировании вязкости смесей, имеющих в своем составе три и более исходных смешиваемых нефтей.
Теоретически решить проблему можно с помощью проведения предварительных лабораторных исследований по определению вязкости смесей нефтей во всех возможных пропорциях смешения. Но таких различных смесей может сформироваться бесконечно много, поэтому проводить лабораторное определение вязкости для каждой из смесей нефтей даже с некоторой дискретностью долей смешения является неоправданно трудоемко. Наиболее оптимальным решением указанной проблемы может стать разработка метода прогнозирования вязкости смеси расчетным методом без проведения предварительных лабораторных испытаний.
Основная идея заключается в определении корреляционной зависимости вязкости нефти от других ее физико-химических свойств, которые при смешении нефтей поддаются аддитивному расчету, таких как плотность, содержание высокомолекулярных соединений, фракционный состав и т.п. Определив расчетным способом аддитивные физико-химические свойства смеси, по корреляционной зависимости можно оценить значение ее вязкости.
Для определения указанной выше корреляционной зависимости нами использовалась база данных со свойствами нефтей, описанными в справочнике «Нефти СССР» (1971, 1972, 1974). В этой базе данных имеются сведения о вязкости, плотности, содержании парафина, смол, асфальтенов и фракционном составе 773 видов нефтей, добываемых в 70-е годы XX в. на территории СССР. При этом вязкости приведены при температурах от 0 °С до 70 °С с шагом в 10 °С.
Таким образом, целью настоящей работы является построение корреляционной зависимости вязкости нефти от ее плотности, содержания парафина, смол, асфальтенов и их фракционного состава. Это исследование продолжает серию наших работ (Валеев и др., 2024; Valeev et al., 2024) о прогнозировании вязкости смеси нефтей на основе их других физико-химических свойств, поддающихся аддитивности.
2. Базовая модель прогнозирования вязкости нефти
В качестве базовой модели прогнозирования вязкости взяты полученные нами ранее результаты (Valeev et al., 2024). В рамках настоящего исследования построены уравнения регрессии второго порядка для определения вязкости на основе плотности и содержании парафинов, смол, асфальтенов. Определение содержания таких высокомолекулярных соединений в нефти, как парафинов, смол и асфальтенов, при установлении свойств нефти применяется и в других направлениях исследований (Khuramshina, 2023). Погрешность формул оценивалась с учетом поэлементной кросс-валидации. Кросс-валидация, так же как и другие математические операции, проводилась посредством языка программирования Python. Значения оценки погрешности представлены в табл 2.
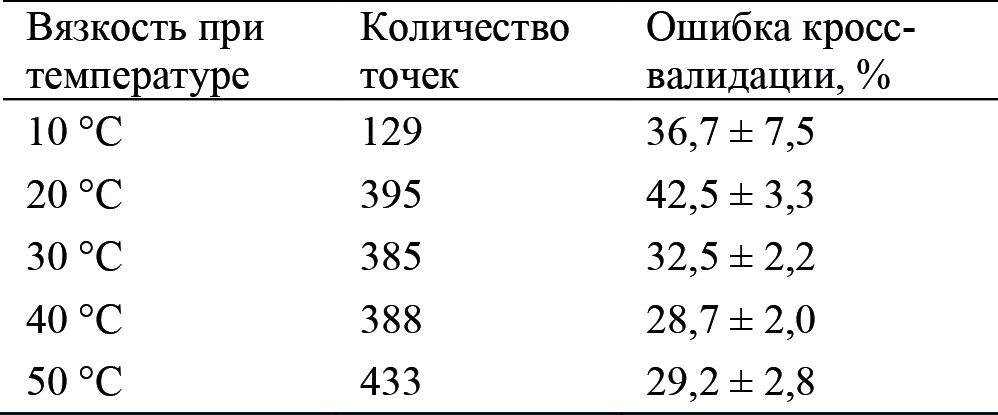
Табл. 2. Оценка ошибки кросс-валидации
при аппроксимации вязкости уравнением регрессии второго порядка
в зависимости от плотности и содержания парафина, смол, асфальтенов
Уравнения регрессии корреляционных зависимостей для определения вязкости при различных температурах имеют следующий вид:
ν10 = exp(–13,4 + 172П – 6,46С – 227А + 5,51ρ20 – 180П2 + 375ПА – 179Пρ20 – 11,1СП – 0,835С2 – 6,84СА + 9,24Сρ20 – 25,9А2 + 245ρ20А + 15,2ρ202), (5)
ν20 = exp(40,0 – 2,30П – 6,78С + 51,6А – 117p20 + 48,6П2 + 51,6ПА + 2,72Пρ20 + 0,650СП – 2,40С2 + 14,6СА + 10,4Сρ20 + 14,5А2 – 76,1ρ20А + 84,6ρ202), (6)
ν30 = exp(63,7 + 24,2П – 14,1С + 88,6А – 167ρ20 – 3,83П2 + 23,9ПА – 23,7Пρ20 – 0,762СП – 3,57С2 + 14,6СА+ 20,2Сρ20 + 11,3А2 – 113ρ20А + 110ρ202), (7)
ν40 = exp(44,8 + 34,6П – 23,2С + 97,4А – 119ρ20 – 3,14П2 + 17,5ПА – 37,9Пρ20 – 0,744СП – 3,51С2 + 9,74СА + 30,7Сρ20 + 8,68А2 – 119ρ20А + 79,1ρ202), (8)
ν50 = exp(16,6 + 65,7П – 25,1С + 99,4А – 52,7ρ20 – 0,473П2 + 0,462ПА – 80,4Пρ20 + 11,3СП – 3,22С2 + 12,3СА + 31,8Сρ20 + 10,1А2 – 123ρ20А + 40,9ρ202), (9)
где вязкости ν10–ν50 представлены в размерности сСт, содержания парафинов (П), смол (С), асфальтенов (А) – в долях единицы, плотность ρ20 – в т/м³.
Представленные в табл. 2 погрешности вязкости имеют значения порядка 30–40%. На первый взгляд, такие значения кажутся слишком большими, но при расчете энергопотребления и потерь напора трения погрешность станет мельше. Например, потери напора при перекачке нефти по трубопроводу в турбулентном режиме в зоне гидравлически гладких труб (наиболее характерной для магистральных нефтепроводов) зависят от вязкости в степени 0,25 (согласно формуле Лейбензона (Белоусов, Сафонов, 1971)), поэтому и потери напора будут определяться с погрешностью около 7–10%.
Указанные значения погрешности в 30–40% будут являться сравнительной характеристикой для дальнейших исследований, представленных в рамках настоящей статьи.
3. Прогнозирование вязкости нефти при заданной температуре на основе ее параметров, поддающихся аддитивности
Целью следующего этапа исследований является определение более сложной корреляционной зависимости вязкости нефти при заданной температуре с добавлением в уравнение, кроме плотности, содержания парафинов, смол, асфальтенов и фракционного состава.
Для каждой вязкости при температурах от 10 °С до 50 °С с шагом в 10 °С строились уравнения линейной регрессии и уравнения регрессии второго порядка для логарифма вязкости. Для построения корреляционной зависимости использовалось фракционное содержание для заданной температуры, а также фракционное содержание для заданного диапазона температур. Перебиралось различное сочетание плотности, содержания парафина, смол, асфальтенов, а также фракционного состава. Температуры для фракционного состава принимались согласно ГОСТ 2177-99 (раздел 6, метод «Б»): 100 °С, 120 °С, 150 °С, 160 °С и далее каждые 20 °С до 300 °С. Общее количество моделей, которые анализировались, составило 4220 (без учета объема выборки для кроссвалидации).
Были определены оптимальные аргументы для анализа: фракционное содержание для заданной температуры (модель 1) или содержание для заданного диапазона температур (модель 2).
В модели 1 использовалась регрессия второго порядка, а в качестве аргумента бралось фракционное содержание для заданной температуры, а также плотность, содержания смол, фракционное содержание до 300 °С.
В модели 2 также использовалась регрессия второго порядка, а в качестве аргумента учитывались значения плотности, содержаний смол, фракционного содержания до 150 °С, а также в диапазонах 150–220 °С и 220–300 °С. В табл. 3 приведены результаты сравнения. Погрешность формул оценивалась с учетом поэлементной кросс-валидации. Модель 1 показала лучший результат.
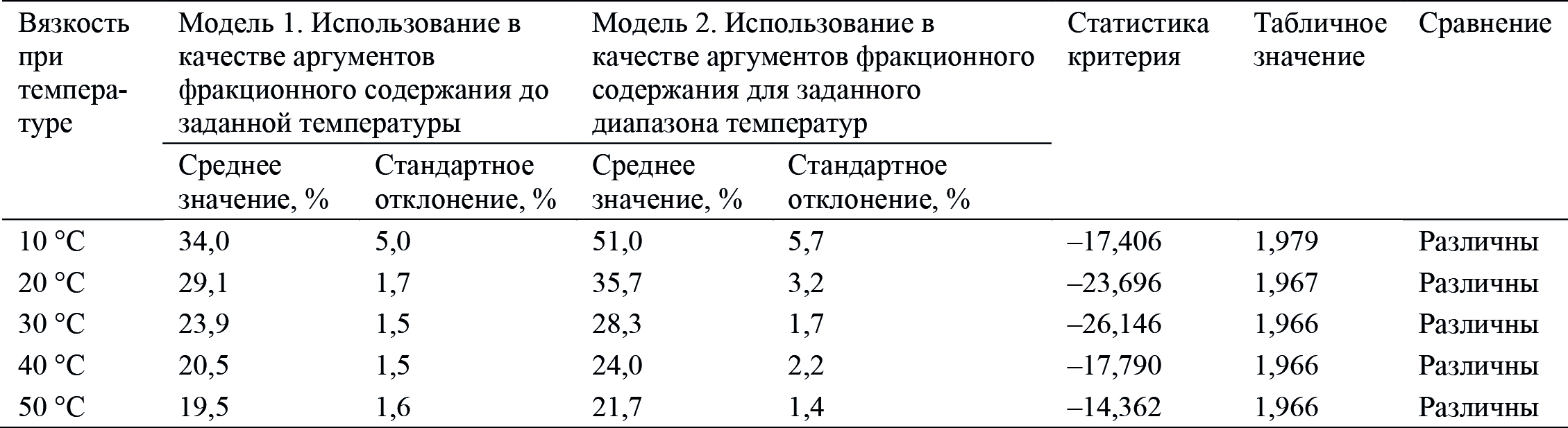
Табл. 3. Сравнение погрешности наиболее точных полученных регрессий
с информацией о фракционном содержании до заданной температуры
или содержании для заданного диапазона температур
Как видно из таблицы, у модели 1 погрешность ниже, и данное отличие статистически значимо практически для всего диапазона температур (на основе двухвыборочного t-критерия Стьюдента при уровне значимости 0,05).
Таким образом, целесообразнее использовать фракционное содержание для заданной температуры, чем для диапазона температур. В таком же виде информация представлена и в справочнике «Нефти СССР».
В целях поиска наиболее подходящих параметров для определения вязкости проводился перебор комбинаций линейной регрессии второго порядка с различным набором параметров. Количество таких комбинаций составило 4220. В табл. 4 представлена информация по погрешности лучших уравнений для определенной вязкости при заданной температуре.

Табл. 4. Погрешности при определении вязкости при заданной температуре
в зависимости от плотности, содержания парафина, смол, асфальтенов,
а также от фракционного состава
Новые уравнения регрессии корреляционных зависимостей для определения вязкости при различных температурах будут вид
ν10 = exp(–26,8 + 34,9ρ20 + 0,0350С – 4,38А – 42,1Ф120 + 7,15Ф300), (10)
ν20 = exp(–128 + 244П + 219ρ20 – 6,31С – 254Ф260 + 327Ф300 + 25,0П2 – 261Пρ20 – 186ПФ260 + 101ПФ300 – 73,7ρ202 + 330p20Ф260 – 413ρ20Ф300 + 3,86СП – 1,59Сρ20 + 2,24С2 – 28,9СФ260 + 35,9СФ300 + 239Ф2602 – 401Ф300Ф260 + 163Ф3002), (11)
ν30 = exp(116 – 266ρ20 – 18,6С – 431Ф280 + 389Ф300 + 162ρ202 + 507ρ20Ф280 – 474ρ20Ф300 + 17,5Сρ20 – 0,0177С2 – 21,7СФ280 + 28,1СФ300 + 225Ф2802 – 400Ф300Ф280 + 183Ф3002), (12)
ν40 = exp(147 – 345ρ20 – 77,2Ф180 – 87,1Ф240 + 97,4Ф300 + 208ρ202 + 60,2ρ20Ф180 + 126ρ20Ф240 – 123ρ20Ф300 + 11,7Ф1802 – 112Ф240Ф180 + 129Ф2402 + 122Ф300Ф180 –172Ф300Ф240 + 35,0Ф3002), (13)
ν50 = exp(18,2 – 29,1ρ20 – 27,8С – 9,52Ф300 + 15,1ρ202 + 0,645ρ20Ф300 + 33,1Сρ20 – 1,63С2 + 2,42СФ300 + 4,49Ф3002), (14)
где выход фракции до 260 °С (Ф260) и 300 °С (Ф300) – в долях единицы.
4. Прогнозирование вязкости нефти на основе формулы Филонова – Рейнольдса и свойств нефти, поддающихся аддитивности
Полученные расчетные значения вязкости позволяют пересчитать вязкость и при других температурах с помощью, например, формул Филонова–Рейнольдса, Вальтера или Фогеля–Фульчера–Таммана. Поскольку эти формулы содержат в себе эмпирические коэффициенты, в них подставляются предварительно измеренные значения вязкости при заданных двух-трех величинах температуры. С учетом того, что в полученных уравнениях используются различные параметры, то имеем некоторое затруднение при выборе конкретных зависимостей среди уравнений (10)–(14).
Поскольку уже найдены вязкости при определенных температурах, то предлагается использовать формулу Филонова–Рейнольдса в качестве основы для искомой зависимости. Для того чтобы ее применять, необходимо уравнение для расчета коэффициента крутизны вискограммы (u).
На основе имеющих сведений о вязкости нефтей из базы данных определили коэффициент крутизны вискограммы и выбрали оптимальную зависимость для его расчета. Аналогично проведенному выше алгоритму, провели глубокой перебор уравнений регрессий первого и второго порядка с коэффициентами, в качестве которых могут выступать плотность, содержания парафинов, смол, асфальтенов и их фракционное содержание. В итоге оптимальным уравнением оказалось следующее:
u = 0,0462 + 0,277П + 0,0351С – 0,122Ф200 + 0,238П2 – 0,241ПФ200 – 0,478СП – 0,00440С2 – 0,0565СФ200 + 0,0885Ф2002. (15)
Таким образом, уравнения (10)–(14) могут использоваться для расчета вязкости при заданной температуре, а уравнение (15) – для расчета коэффициента крутизны вискограммы. Для расчета вязкости по уравнению Рейнольдса – Филонова необходимо знать значение вязкости при определенной температуре. Было проведено сравнение, при какой температуре предпочтительнее использовать известное значение вязкости для наиболее точного определения вязкостно-температурной зависимости. Для этого получили расчетные значения вязкости по различным формулам и сравнили с фактическими значениями вязкости из базы данных. Погрешности определения вязкости представлены в табл. 5.
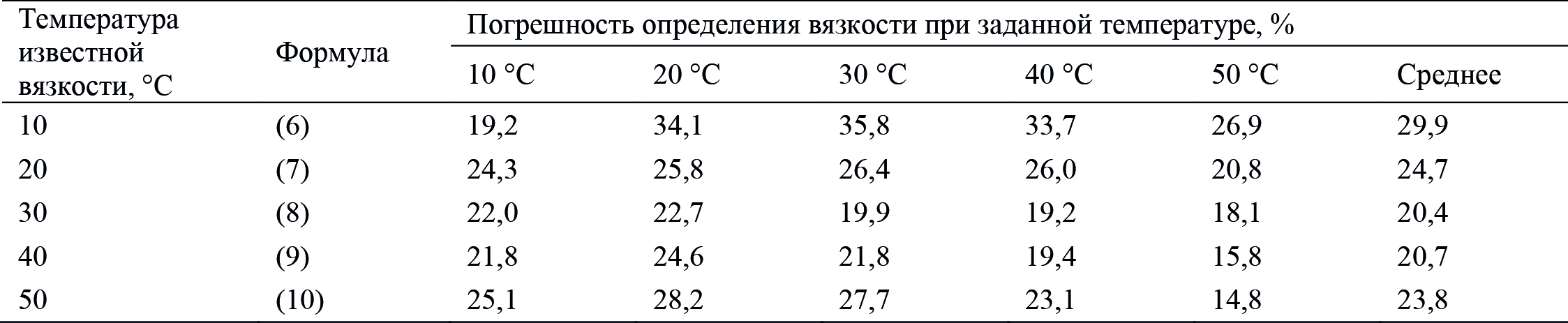
Табл. 5. Погрешность определения вязкости
при использовании уравнения Филонова – Рейнольдса и сведений о плотности,
содержании парафина, смол, асфальтенов, а также о фракционном составе
Из табл. 5 видно, что наименьшая погрешность 20,4% наблюдается при применении формулы Рейнольдса – Филонова для вязкости при температуре 30 °С. Таким образом, формула Рейнольдса – Филонова для определения вязкости v(t) при температуре t имеет следующий вид:
v(t) = ν30 exp[–u(t – 30)], (16)
где ν30 определяется по формуле (12), а коэффициент крутизны вискограммы по формуле (15).
Согласно зависимости (16) вязкость при заданной температуре определяется по плотности, содержании парафинов, смол, а также по фракционному составу до 200 °С, 280 °С и 300 °С.
В соответствии с проведенными нами исследованиям (Валеев и др., 2024) уравнение Филонова – Рейнольдса имеет в среднем погрешность 13,8% при прогнозировании вязкости нефти. Таким образом, применение формулы (16) повышает погрешность определения вязкости только на 6,6% по сравнению с вязкостью, устанавливаемой при лабораторных испытаниях.
5. Заключение
В настоящей работе предложены эмпирические уравнения для определения вязкости нефти с использованием таких параметров, как плотность нефти, содержание асфальтенов, смол и парафинов, доля выхода фракции при заданной температуре. Поскольку данные параметры аддитивны, после их определения для смеси вязкость смеси также становится определяемой по полученной зависимости.
На основе имеющейся базы данных о свойствах нефтей и перебора большого количества различных регрессий первого и второго рода построены зависимости для определения вязкости при температурах 10 °С, 20 °С, 30 °С, 40 °С, 50 °С. Они имеют погрешность 20–27%, которая оценена при помощи поэлементной кросс-валидации. В качестве исходных данных для расчета вязкости бралась информация о плотности, содержании парафинов, смол, асфальтенов, а также о их фракционном составе.
Построено уравнение для расчета вязкости при любой температуре, основанное на формуле Филонова – Рейнольдса. При расчете вязкостей в диапазоне 10–50 °С уравнение дает погрешность 20,4%, оцененную с помощью кросс-валидации. В качестве исходных данных для расчета также использовалась информация о плотности, содержании парафинов, смол, а также о их фракционном содержании до 200 °С, 280 °С и 300 °С.
С использованием полученных зависимостей можно будет определять вязкость смеси нефти в любой точки разветвленной сети нефтепроводов, когда известны только свойства нефти на входе в данную сеть (например, после пункта подготовки нефти), и пропорции смешения нефтей в узловых точках. Такой подход позволит сократить объем лабораторных исследований по определению вязкости смесей нефтей, повысить качество прогнозирования технологических режимов перекачки нефти, принимать верные управленческие решения за счет наличия более точной информации. В совокупности полученные результаты могут повысить экономические показатели нефтяной отрасли в целом и трубопроводного транспорта нефти в частности.
Отметим, что сделанные выводы основаны на определенной базе данных, а следовательно, при большем объеме информации результаты могут измениться, а некоторые значения могут быть получены с меньшей точностью.
Финансирование
Исследование выполнено за счет гранта Евразийского научно-образовательного центра (проект № ЕНОЦ-06-22).
Список литературы
1. Аралов О.В., Буянов И.В., Саванин А.С., Иорданский Е.И. (2017). Исследование методов расчета кинематической вязкости нефти в магистральном нефтепроводе. Наука и технологии трубопроводного транспорта нефти и нефтепродуктов, 7(5), с. 97–105.
2. Белоусов В.Д., Сафонов, В.С. (1971). Определение потери напора на трение в области смешанного трения по формуле Л.С. Лейбензона. Транспорт и хранение нефти и нефтепродуктов, (8), с. 9–12.
3. Валеев А.Р., Ташбулатов Р.Р., Барабанщикова Т.А. (2024). Определение оптимальных температур измерения вязкости нефти для восстановления ее вязкостно-температурной зависимости по формулам Филонова-Рейнольдса, Вальтера и Фогеля–Фульчера–Таммана. Известия Томского политехнического университета. Инжиниринг георесурсов, 335(4), с. 131–138. https://doi.org/10.18799/24131830/2024/4/4283
4. Закиров А.И. (2016). Обоснование режимов трубопроводного транспорта битуминозной нефти: Дис. … канд. техн. наук. СПб., 170 с.
5. Нефти СССР . (1971). Справочник. Т. 1: Нефти северных районов Европейской части СССР и Урала. Под ред. З.В. Дриацкой, Е.Г. Ивченко, Е.Г. Ивченко, М.А. Мхчиян. М.: Химия, 504 с.
6. Нефти СССР . (1972). Справочник. Т. 2: Нефти Cреднего и Нижнего Поволжья. Под ред. З.В Дриацкой, Н.М. Жмыховой, И.С. Лазаревой, М.А. Мхчиян, А.П. Олейниковой. М.: Химия, 392 с.
7. Нефти СССР . (1972). Справочник. Т. 3: Нефти Кавказа и западных районов Европейской части СССР . Под ред. Г.Г. Ашумова, З.В. Дриацкой, Н.М. Жмыховой А.С. Журба, Е.С. Левченко, М.А. Мхчиян. М.: Химия, 616 с.
8. Нефти СССР . (1974). Справочник. Т. 4: Нефти Средней Азии, Казахстана, Сибири и о. Сахалин. Под ред. З.В. Дриацкой, Н.М. Жмыховой, М.А. Мхчиян, Г.Х. Ходжаева. М.: Химия, 792 с.
9. Ташбулатов Р.Р. (2019). Прогнозирование вязкостно-температурных характеристик течения смесей при совместной транспортировке различных нефтей в системе магистральных нефтепроводов: Дис. … канд. техн. наук. Уфа, 135 с.
10. Al-Besharah J.M. (1989). The effect of blending on selected physical properties of crude oils and their products. PhD dissertation: University of Aston, Birmingham, Alabama.
11. Al-Maamari R.S., Vakili-Nezhaad G., Vatani M. (2015). Experimental and Modeling Investigations of the Viscosity of Crude Oil Binary Blends: New Models Based on the Genetic Algorithm Method. The Journal of Engineering Research (TJER), 12(1), pp. 81–91. https://doi.org/10.24200/tjer.vol12iss1pp81-91
12. Arrhenius S.A. (1887). Uber die Dissociation der in Wasser gelösten Stoffe. Z Phys Chem, (1), pp. 631–648. https://doi.org/10.1515/zpch-1887-0164
13. Baird C.T. (1989). IV Guide to petroleum product blending. Austin (TX): HPI Consultants, Inc.
14. Bingham E.C. (1918). The variable pressure method for the measurement of viscosity. In: Proceeding of American society for testing materials, 18 (Part II), 10.
15. Cragoe C.S. (1933). Changes in the viscosity of liquids with temperature, pressure and composition. Proc. World Pet Congr, London, 2, pp. 529–541.
16. Chen Y., Jin L., Zhang M., He M. (2023). Experimental study on the rheological characteristics and viscosity-enhanced factors of super-viscous heavy oil. Liquid and Gaseous Energy Resources, 3(2), pp. 67–75. https:// doi.org/10.21595/lger.2023.23660
17. Han S.-p., Jiang W.-x., Zhang, J.-j. (2007). Approaches to Predict Viscosities of Crude Oil Blends. Journal of Central South University of Technology, 14(Suppl. 1), pp. 466–470. https://doi.org/10.1007/s11771-007-0308-5
18. Khan M.A.B., Mehrotra A.K., Svrcek W.Y. (1984). Viscosity Models for Gas-Free Athabasca Bitumen. The Journal of Canadian Petroleum Technology, 23(3), pp. 47–53. https://doi.org/10.2118/84-03-05
19. Khuramshina R. (2023). Analysis of hydrocarbon solvents for the removal of various types of asphalt, resin and paraffin deposits. Liquid and Gaseous Energy Resources, 3(1), pp. 7–13. https://doi.org/10.21595/lger.2023.23373
20. Koval E.J. (1963). A method for predicting the performance of unstable miscible displacement in heterogeneous media. SPE Journal, (3), pp. 145–154. https://doi.org/10.2118/450-PA
21. Langbauer C., Langbauer T., Fruhwirth R., Mastobaev B. (2021). Sucker rod pump frequency-elastic drive mode development – from the numerical model to the field test. Liquid and Gaseous Energy Resources, 1(1), pp. 64–85. https://doi.org/10.21595/lger.2021.22074
22. Maxwell J.B. (1950). Data Book on Hydrocarbons: Application to Process Engineering. Princeton, New Jersey: D. Van Nostrand Company, Inc.
23. Miadonye A., Doyle N.L., Britten A., Latour N., Puttagunta V.R. (2001). Modelling viscosity and mads fraction of bitumen–diluent mixtures. J Can Pet Technol, 40(7), pp. 52–57. https://doi.org/10.2118/01-07-04
24. Miadonye A., Latour N., Puttagunta V.R. (2000). A Correlation for Viscosity and Solvent Mass Fraction of Bitumen-Diluent Mixtures. Petroleum Science and Technology, 18(1–2), pp. 1–14. https://doi.org/10.1080/10916460008949828
25. Miadonye A., Singh B., Puttagunta V.R. (1994). Modeling the Viscosity-Temperature Relationship of Alberta Bitumen. Fuel Science and Technology International, 12(2), pp. 335–350. https://doi.org/10.1080/08843759408916182
26. Miadonye A., Singh B., Puttagunta V.R. (1995). Viscosity Estimation for Bitumen-Diluent Mixtures. Fuel Science and Technology International, 13(6), pp. 681–698. https://doi.org/10.1080/08843759508947700
27. Parkash S. (2003). Refining Processes Handbook. Oxford, UK: Elsevier (Gulf Professional Publishing). https://doi.org/10.1016/B978-075067721-9/50007-4
28. Puttagunta V.R., Singh B., Miadonye A. (1993). Correlation of Bitumen Viscosity with Temperature and Pressure. The Canadian Journal of Chemical Engineering, 71(3), pp. 447–450. https://doi.org/10.1002/cjce.5450710315
29. Riazi M.R. (2005). Characterization and properties of petroleum fractions, first ed. American Society and Testing Materials, ASTM Manual Series: MNL50, USA. https://doi.org/10.1520/MNL50_1ST-EB
30. Shan-peng H., Wen-xue J., Jin-jun Z. (2007). Approaches to predict viscosities of crude oil blends. Journal of Central South University of Technology, (14), pp. 466–470. https://doi.org/10.1007/s11771-007-0308-5
31. Valeev A.R., Tashbulatov R.R., Barabanshchikova T.A. (2024). Recovery of oil viscosity values according to its additive parameters. SOCAR Proceedings, (1), pp. 76–80.
32. Wallace D., Henry D. (1987). A correlation for correcting the viscosity of solvent-extracted bitumen to a solvent-free basis. AOSTRA Journal of Research, (3), pp. 239–249.
33. Zhang C., Zhao H., Hu M., Xiao Q., Li J., Cai C. (2007). A Simple Correlation for the Viscosity of Heavy Oils from Liaohe Basin, NE China Text. The Journal of Canadian Petroleum Technology, 46(4), pp. 8–11. https:// doi.org/10.2118/07-04-TN
Об авторах
А. Р. ВалеевРоссия
Анвар Рашитович Валеев – доктор тех. наук, профессор кафедры «Транспорт и хранение нефти и газа»
450064, Уфа, ул. Космонавтов, д. 1
Р. Р. Ташбулатов
Россия
Радмир Расулевич Ташбулатов – кандидат тех. наук, доцент кафедры «Транспорт и хранение нефти и газа»
450064, Уфа, ул. Космонавтов, д. 1
Я. Чэнь
Китай
Чень Ян – кандидат тех. наук, Ph.D., доцент кафедры «Транспорт и хранение нефти и газа»
610500, Провинция Сычуань, Чэнду, ул. Щинду, д. 8
Р. М. Каримов
Россия
Ринат Маратович Каримов – кандидат тех. наук, доцент кафедры «Транспорт и хранение нефти и газа»
450064, Уфа, ул. Космонавтов, д. 1
Рецензия
Для цитирования:
Валеев А.Р., Ташбулатов Р.Р., Чэнь Я., Каримов Р.М. Прогнозирование вязкостно-температурной зависимости смеси нефтей по информации об их плотности, содержании парафина, смол, асфальтенов и фракционном составе. Георесурсы. 2024;26(3):232-239. https://doi.org/10.18599/grs.2024.3.23
For citation:
Valeev A.R., Tashbulatov R.R., Chen Y., Karimov R.M. Prediction of the Viscosity-Temperature Dependence of a Mixture of Oils Based on Information about the Density, Content of Paraffin, Resins, Asphaltenes and Fractional Composition. Georesursy = Georesources. 2024;26(3):232-239. (In Russ.) https://doi.org/10.18599/grs.2024.3.23















.png)


