Перейти к:
Применение искусственных цифровых моделей в методе рентгеновской томографии керна при решении задачи бинаризации пустотного пространства горных пород
https://doi.org/10.18599/grs.2024.4.11
Аннотация
Метод рентгеновской томографии обладает рядом преимуществ, заключающихся в неразрушающем способе воздействия на образец и возможности объемной визуализации скелета породы и емкостного Пространства. При этом проблемой, Ограничивающей Возможности Практического Использования Томографии, является низкая разрешающая способность при исследовании образцов диаметром 30 мм. В образцах таких размеров существенная часть пор имеет размеры меньшие, чем разрешающая способность большинства современных систем рентгеновской томографии, что не позволяет определить граничное значение пора – скелет в томограммах керна и визуализировать весь объем емкостного пространства. Для подтверждения этого проанализированы томограммы реальных образцов коллекторов нефти и газа. Анализ полученных гистограмм условной рентгеновской плотности позволил прийти к выводу, что прямое определение граничного значения условной рентгеновской плотности, характеризующей границу пора – скелет, невозможно.
Для решения проблемы оценки граничного значения в работе предложен подход, предлагающий применение искусственных цифровых моделей – фантомов. Эта методика ранее использовались преимущественно в компьютерном моделировании, в нефтяной геологии такой подход практически не применялся. Главным достоинством метода использования фантомов является полный контроль задаваемых параметров порового пространства и рентгеновской плотности скелета, что принципиально не достижимо на реальных образцах. Проведен вычислительный эксперимент, в ходе которого с помощью численного моделирования созданы 124 фантома керна с заданными характеристиками пористости. Эксперимент позволил установить статистические характеристики для значений условной рентгеновской плотности образца, получаемых на этапе реконструкции.
На основе результатов эксперимента определены граничные значения, пригодные для наиболее достоверного выделения пустотного пространства. При помощи регрессионного и корреляционного анализа предложена модель оценки оптимального граничного значения условной рентгеновской плотности для выделения пустотного пространства. Предложен алгоритм, позволяющий определять и использовать это значение при обработке и анализе данных рентгеновской томографии керна.
Результаты представленной методики использованы для оценки структуры пустотного пространства реальных образцов керна, которые не привлекались для создания модели прогноза. Применение разработанной модели прогноза граничных значений продемонстрировало высокую корреляцию с фактическими данными.
Ключевые слова
Для цитирования:
Мелкишев О.А., Савицкий Я.В., Галкин С.В. Применение искусственных цифровых моделей в методе рентгеновской томографии керна при решении задачи бинаризации пустотного пространства горных пород. Георесурсы. 2024;26(4):218-228. https://doi.org/10.18599/grs.2024.4.11
For citation:
Melkishev O.A., Savitsky Y.V., Galkin S.V. The Application of Artificial Digital Models in X-Ray Computed Tomography (CT) of the Core in Solving the Problem of Binarization of the Void Space of Reservoir Rocks. Georesursy = Georesources. 2024;26(4):218-228. (In Russ.) https://doi.org/10.18599/grs.2024.4.11
Введение
Включение рентгеновской томографии керна в практику петрофизических исследований приобретает в настоящее время все большее распространение. Одним из главных достоинств метода является возможность визуализации порового пространства, что позволяет проводить не только количественное измерение объема порового пространства, но и измерять диаметры пор, их форму, площадь, степень извилистости, локализовать неоднородности их распределения в образцах. Помимо этого, метод в объеме дает возможность характеризовать минералогические (литологические) особенности скелета горной породы. Совокупность данных томографии позволяет создавать модель образца керна и проводить численное моделирование экспериментов по измерению проницаемости (Denney, 2004; Fernandes et al., 2012).
Несмотря на длительную историю применения метода в нефтяной геологии (Vinegar, 1986; Denney, 2004; Еременко, Муравьева, 2012; Кривощёков, Кочнев, 2013), наиболее эффективным стало применение рентгеновской томографии в основном для исследования методов интенсификации добычи углеводородов (Djimasbe et al., 2022; Prasad et al., 2023), в частности для изучения эффективности воздействий кислотных составов (Shameem Siddiqui et al., 2006; Manazael Zuliani Jora et al., 2021; Дмитриева и др., 2018; Мартюшев, Новиков 2020; Галкин и др., 2020) и для изучения особенностей заполнения пропантом трещин гидроразрыва пластов (Marco Voltolini et al., 2021; Hamed Lamei Ramandi et al., 2021; Galkin et al., 2023). Все эти задачи связаны с оценкой крупных пустот размером более 0,1 мм, относящихся к сверхкапиллярному классу, что позволяет с высокой степенью достоверности визуально отделить на томограммах образцов скелет горной породы от порового пространства.
При этом выделение пустотного пространства и изучение его структуры тесно связано со значениями закрытой пористости, наличием и размерами открытых пор, поровых каналов и тупиковых пор. Все эти характеристики связаны с капиллярными давлениями, остаточной водо- и нефтенасыщенностью. Такие характеристики влияют на коэффициент вытеснения, а следовательно, и коэффициент извлечения нефти (КИН), как один из основных параметров подсчета запасов углеводородов и ключевая характеристика системы разработки залежи.
При решении задач изучения структуры порового пространства пластов-коллекторов, возникают проблемы достоверной оценки пустотного объема образцов керна стандартного диаметра 30 мм. Эта проблема вызвана комплексным влиянием ряда причин: размерами образца, особенностями физического взаимодействия рентгеновского излучения и материала скелета, особенностями аппаратного обеспечения (конструкцией и характеристиками рентгеновского томографа), особенностями алгоритмов реконструкции изображений, субъективностью ряда граничных характеристик при интерпретации результатов. Совокупность таких причин не позволяет в итоговых реконструированных кубах четко произвести бинаризацию, то есть отделить пустотное пространство от скелета породы (Manu K. Mohan et al., 2023).
Рассмотрим принцип действия метода рентгеновской томографии. Метод основан на получении серии рентгеновских изображений объекта, из которых с помощью программных методов получают объемное изображение. Для создания серии снимков образец помещают в держатель, который вращается с заданным шагом вокруг одной из осей, как правило, вертикальной, на 360°. Программой съемки определяется количество снимков (2D проекций) и время экспозиции каждого снимка. Снимок формируется на цифровой кремниевой матрице детектора, установленной напротив рентгеновской трубки, и представляет собой пиксельное изображение. Таким образом, создается серия рентгеновских снимков, которая в результате процедуры реконструкции преобразуется в объемную модель (рис. 1). Снимок представляет собой полутоновые изображения, в которых яркость пикселя характеризует степень поглощения рентгеновского излучения в результате фотоэффекта и комптоновского рассеяния. Степень поглощения зависит от физических свойств горной породы, чаще всего плотности.
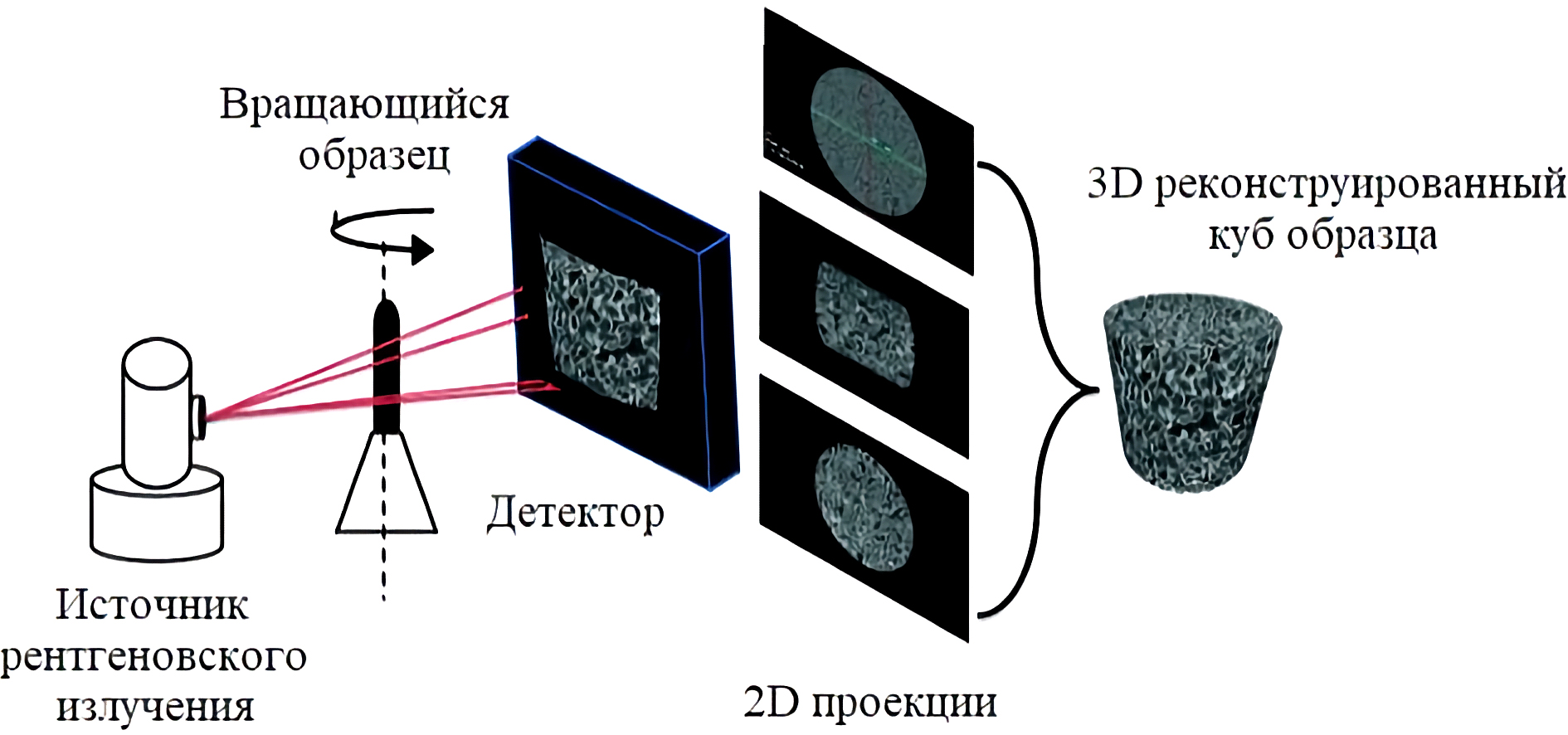
Рис. 1. Схема проведения процедуры рентгеновской томографии
Преобразование двухмерных снимков (2D проекций) в трехмерное изображение происходит с помощью различных алгоритмов реконструкции (Katsevich, 2004; Van Aarle et al., 2016), таких как FBP1, SIRT2, SART3, CGLS4, ART5.
Итоговое качество объемной модели образца после реконструкции зависит от количества снимков и самого алгоритма реконструкции, характеристик работы рентгеновской трубки (сила тока и напряжение).
Процесс изучения керна горных пород состоит из следующих этапов, на каждом из которых проявляется ряд факторов, влияющих в той или иной степени на конечный результат:
- изготовление образца, его экстрагирование или экстрагирование и насыщение рентгеноконтрастным веществом (геометрические размеры и форма образца);
- съемка образца (геометрия съемки, напряжение и сила тока в рентгеновской трубке);
- реконструкция (алгоритмы предобработки изображения проекций, сам алгоритм реконструкции);
- обработка реконструированного куба и интерпретация результатов (фильтрация реконструированного куба, граничные значения бинаризации – отсечки);
- получение итоговых характеристик образца (коэффициент пористости, распределение диаметра пор и их формы, коэффициенты связанности и др.).
В процессе проведения вышеперечисленных операций неизбежно происходит снижение качества и точности получаемого изображения. Причинами ухудшения изображений являются артефакты и шум (Van Aarle et al., 2015; Ketcham, Hanna, 2014; Romano et al., 2019). Таким образом, низкая разрешающая способность метода для образцов стандартного размера вкупе с наличием артефактов и шума сильно осложняют интерпретацию итогового результата.
Различные исследователи предлагают возможные варианты решений, например, комплексирование методов томографии и электронной микроскопии (Shah et al., 2013; Чугунов и др., 2015; Осовецкий и др., 2023) или же целого комплекса исследований, включающего капилляриметрию и ЯМР (Чистяков и др., 2022). При этом применение дополнительных исследований существенно усложняет процесс оценки порового пространства, в том числе в связи с различной масштабностью таких исследований. В основу статьи частично легли материалы диссертационного исследования одного из авторов (Савицкий, 2023).
Целью настоящей работы является разработка и обоснование методики оценки граничного значения условной рентгеновской плотности для выделения порового пространства пород-коллекторов. Поставлены следующие задачи: проведение компьютерной рентгеновской томографии керна, статистический анализ полученных значений объемных моделей, проведение вычислительного эксперимента с целью создания модели прогноза граничного значения условной рентгеновской плотности для выделения пустотного пространства и проверка полученной модели на фактическом материале.
Материалы и методы
В работе проведен анализ результатов томографических съемок (томограмм) керна. Для анализа использованы образцы керна, представленного терригенными породами месторождений Пермского края. Для всех образцов определена пористость по методу газоволюметрии, для определения пористости использовался порозиметр-пермеаметр AP-608 (Сoretest Systems, США).
Рентгеновская томография керна проводилась с помощью установки компьютерной рентгеновской томографии Nikon XT H 225 (Nikon Metrology, Великобритания). Рабочая разность потенциалов установки – от 30 до 225 кВ, возможность изменения расстояния от источника до приемника – в диапазоне до 1000 мм.
Рентгеновская съемка проводилась при параметрах напряжения 120–180 кВ, силе тока 60–130 мА. Переменные параметры напряжения и тока объясняются техническими особенностями рентгеновской съемки, зависящими от множества факторов, таких как геометрические параметры образца, его плотность и конфигурация положения внутри томографа. Экспозиция кадра во всех случаях составляла 1000 миллисекунд, параметр гейна равен 1, для фильтрации низкоэнергетического излучения использовался медный фильтр толщиной 0,5 мм, количество снимков (2D проекций) – 2000 шт. Реконструкция образцов осуществлялась с помощью проприетарной программы Nikon Metrology CT Pro 3D, подготовка реконструкций – в программе Avizo Fire.
Таким образом, для каждого реального образца создана объемная модель в виде куба, где каждому вокселю объемной модели присвоено значение условной рентгеновской плотности. Гистограммы условной рентгеновской плотности реконструированных кубов по 26 образцам терригенных пород с пористостью от 11 до 20% приведены на рис. 2.
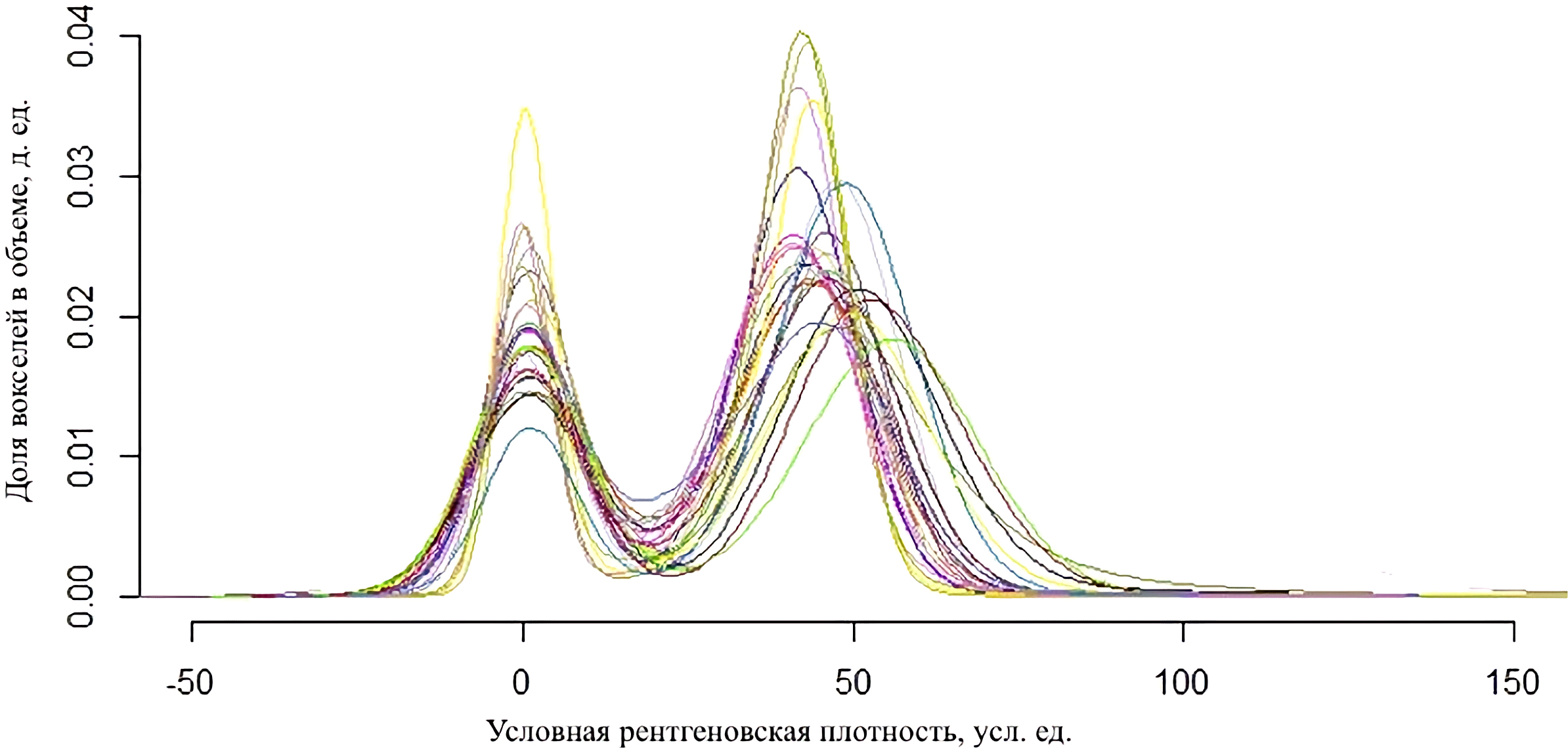
Рис. 2. Гистограммы условной плотности (26 стандартных образцов)
Гистограммы, получаемые после реконструкции (которые содержат образец и воздух вокруг него), имеют 2 моды. Левая мода, характеризующая воздух вокруг образца и в его поровом пространстве, имеет значение близкое к 0 усл. ед. (из-за особенностей алгоритмов реконструкции). Правая мода, характеризующая в основном скелет породы, лежит в диапазоне от 30 до 60 усл. ед. (рис. 2).
Правая часть гистограмм имеет менее симметричную форму и зависит от физических размеров зерен образца и физического размера вокселя реконструированного изображения, коэффициентов поглощения рентгеновского излучения минералами, входящими в состав скелета породы, физической однородности образца (слоистость, минеральные и плотные включения).
Предварительный статистический анализ результатов съемок образцов керна стандартного размера показывает наличие слабой обратной зависимости между медианным значением условной плотности реконструированного образца и пористостью. Такая зависимость имеет низкое значение парного коэффициента корреляции r = –0,48, при достигаемом уровне значимости p = 0,0003 (рис. 3).
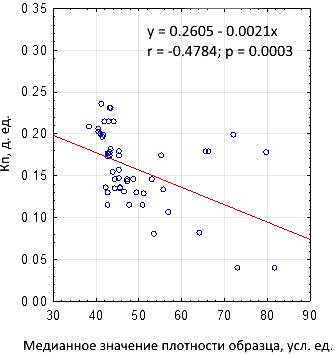
Рис. 3. Зависимость коэффициента пористости от медианной плотности образца
Достаточно низкое значение r указывает на то, что корреляционное поле характеризуется значительной неоднородностью. Это не позволяет напрямую использовать метод регрессионного анализа для определения пористости и связанного с ним граничного значения отсечки в обосновании границы бинаризации пора – скелет, что связано с параметрами съемки (напряжение и сила тока в рентгеновской трубке), вариациями минералогического состава образцов, особенностями процедур реконструкции.
Имеющиеся 2 моды позволяют получить один из вариантов граничного значения условной рентгеновской плотности (отсечки), определяющей границу между скелетом и порой (пустотным пространством) (Савицкий, Галкин, 2021). Впрочем, данный метод имеет ряд недостатков, связанных с учетом вокселей, расположенных вне образца горной породы.
Следовательно, необходимо разработать методику оценки граничного значения отсечки, которая будет основана на объеме, относящемся исключительно к образцу керна. Значение условной рентгеновской плотности для вокселя реконструированного куба зависит от наличия пустот в пределах вокселя, неоднородности характеристик поглощения минеральным скелетом (различный минералогический состав в пределах вокселя), стабильности рентгеновского пучка (постоянный спектр), особенностей алгоритма реконструкции (размера вокселя в реконструкции, округления при расчетах и т.д.).
Таким образом, для реальных образцов керна невозможно точно сопоставить получаемые характеристики реконструкций с исходными образцами. На взгляд авторов, перспективным направлением решения данной проблемы является использование искусственных моделей образцов керна – физических фантомов, с заранее известными моделируемыми характеристиками пустотного пространства и рентгеновской плотности скелета.
Вместе с тем, применение искусственных физических фантомов не нашло широкого распространения в томографии керна, т.к. невозможно изготовить высококачественные модели керна с точно известным геометрическим положением пор, точно заданной формой, размерами и сообщаемостью, наличием микропористостости в скелете. Вследствие чего и получение отсечки с использованием эталонной физической модели керна практически невозможно. Вдобавок, сама процедура реконструкции вносит некоторый разброс значений условной рентгеновской плотности.
Поэтому для разработки методики оценки граничного значения условной рентгеновской плотности необходимо проводить вычислительный эксперимент на цифровом фантоме керна фантом полностью цифровой модели с заданными характеристиками. Подобные модели часто используют в биомедицине (Jamie Lea Pointon et al., 2023), при исследованиях горных пород они имеют более ограниченное применение (Kingston et al., 2018; Chukalina et al., 2021; Eric J. Goldfarb et al., 2022).
Исходя из вышеизложенного, разработан план вычислительного эксперимента, состоящий из следующих этапов:
- генерация цифрового фантома керна;
- процедура прямой проекции;
- внесение шума в проекции;
- реконструкция томограммы образца по зашумленным проекциям;
- ремасштабирование (усреднение) реконструированной модели;
- построение распределений (гистограмм) условной рентгеновской плотности для всего образца и раздельно для порового пространства и скелета фантома;
- расчет различных статистических характеристик и обоснование различных граничных значений по распределениям условной рентгеновской плотности образца.
Код программы, реализующий вычислительный эксперимент, написан на языке программирования Python.
Этап 1. На первом этапе генерируется фантом с известными характеристиками. Для проведения эксперимента генерировались фантомы с пористостью (КП, д.ед.) примерно: 0,025; 0,05; 0,075; 0,1; 0,125; 0,15; 0,175; 0,2; 0,225; 0,25; 0,275; 0,3; 0,325. Такие значения перекрывают диапазон пористости реальных терригенных коллекторов нефти и газа.
Фантом задается кубом размером 400×400×400 вокселей, где находится цилиндрический образец, включающий скелет и поры. Плотность материала скелета подчиняется распределению рентгеновской плотности, имитирующей реальные образцы. Пористость и распределение пустот в пространстве фантома моделировалась в виде случайно расположенных крупных пор размерами 2×2×2, 3×3×3 и 4×4×4 вокселей, и мелких пор размерами 1×1×1 воксель. При этом соблюдалось процентное преобладание в породе мелких пор (75–95 %), а доля крупных пор различного размера задавалось различным процентным соотношением. Значения фактической моделируемой пористости (КП-факт, д.ед.) находятся в интервале от 3,5 до 32 %. Такое моделирование приводит к появлению пор различных размеров и конфигураций.
Значения плотности вокселей скелета фантома (pl, усл.ед.) задаются усеченным нормальным распределением с математическим ожиданием (средним значением) в интервале 49–55 усл.ед. и среднеквадратическим отклонением 0,4–3,6 усл.ед. в соответствии с эмпирическими данными, полученными на реальных образцах при томографических исследованиях образцов 30-миллиметрового керна. Для небольшого количества фантомов плотность скелета задавалась в виде равномерного распределения. При генерации фантомов предусматривалось дополнительное случайное снижение плотности вокселя скелета фантома на величину от 0 до 10% для вокселей, окружающих пору. Для воздуха в поровом пространстве плотность задавалась как постоянная небольшая величина.
На рисунке 4 приведены горизонтальные сечения модели фантома с КП-факт = 0,125 д.ед. и средним значением pl = 55 усл.ед., его реконструкция и ремасштабированный фантом.
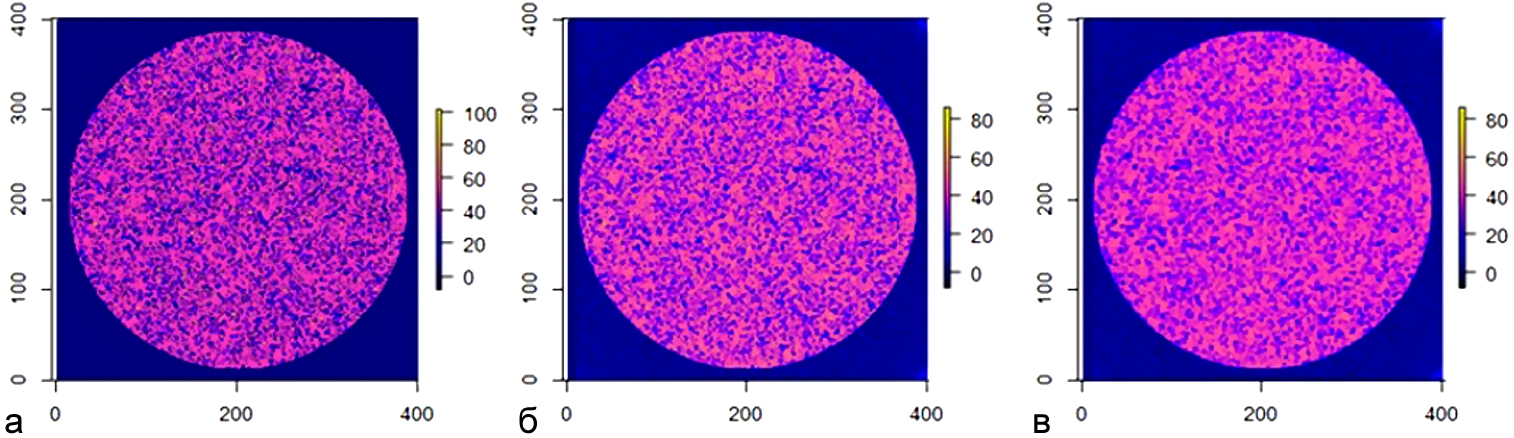
Рис. 4. Горизонтальное сечение (слайс) фантома и его реконструкция с КП-факт = 0,125 д.ед.: а) исходный фантом; б) реконструированный фантом; в) ремасштабированный реконструированный фантом
На рис. 5 приведены гистограммы распределения условной рентгеновской плотности: куба фантома, куба реконструированного фантома и куба ремасштабированного реконструированного фантома. Первая гистограмма (рис. 5а) показывает исходное распределение плотности в фантоме, на ней хорошо видны левый пик, соответствующий воздуху в пустотном пространстве, правый пик, соответствующий основной части скелета, и небольшое количество вокселей с другими значениями плотности.
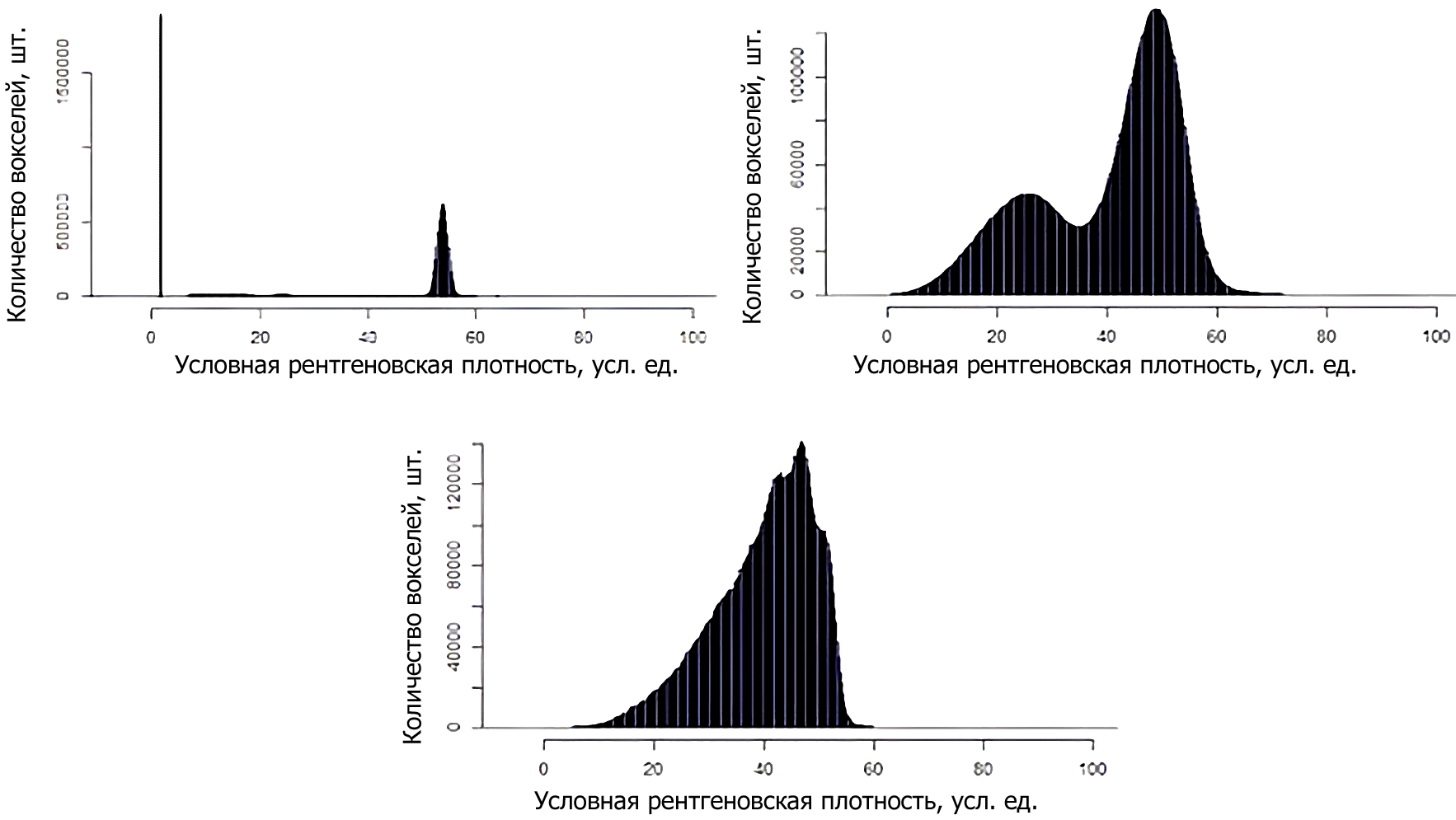
Рис. 5. Гистограммы распределения условной рентгеновской плотности фантома и реконструкции с пористостью 0,125 д.ед. а) исходный фантом; б) реконструированный фантом; в) ремасштабированный реконструированный фантом
Этап 2. Далее при помощи прямой проекции (рис. 1) происходит генерация 2000 снимков (2D проекции) фантома с использованием геометрии конусного луча (cone beam). Геометрические характеристики при данной процедуре аналогичны реальной геометрии съемки, используемой для керна стандартного размера на томографе. Расстояние источник-образец и расстояние образец-детектор обеспечивают сопоставимость угловых величин при проецировании на детектор.
Этап 3. Для еще большей сопоставимости вычислительного эксперимента с реальными данными в каждую прямую проекцию внесен шум Пуассона (рис. 6). Параметр λ в распределении Пуассона задавался таким образом, чтобы обеспечить равенство среднеквадратического отклонения сигнала на 2D проекции фантома вне образца со среднеквадратическим отклонением сигнала на 2D проекции реальных съемок керна.
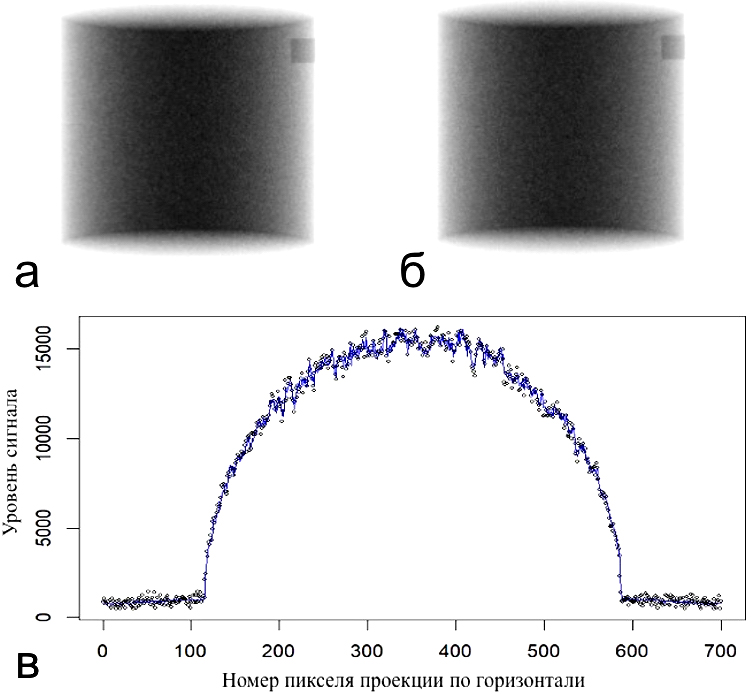
Рис. 6. Пример прямых 2D проекций без шума и с шумом Пуассона: а) прямая проекция; б) прямая проекция с шумом; в) сопоставление сигнала (синяя линия – прямая проекция, черные точки – прямая проекция + шум Пуассона)
Этап 4. Реконструкция томограмм фантома по зашумленным проекциям (обратная проекция) производилась методом FDK (Feldkamp et al., 1984) с использованием библиотеки ASTRA v2.1.0 (Van Aarle et al., 2015, 2016).
Наиболее часто при реконструкциях рентгеновских томографических изображений 3D для конусного луча (cone beam) применяют метод FDK. Тем не менее на практике реализация данного метода в различном программном обеспечении может отличаться друг от друга из-за встроенных в расчетные библиотеки алгоритмов улучшения качества изображений и оптимизации расчетов (Wenxuan Liang et al., 2010; Abella et al., 2012; Soimu et al., 2008; Jun Feng et al., 2013).
После реконструкции соотношение сигнал-шум для образца становится меньше. Итогом процедуры реконструкции является объемная модель условной рентгеновской плотности в виде куба 400×400×400 вокселей (рис. 4б, 5б).
Этап 5. Далее полученные фантомы подвергались процедуре ремасштабирования (усреднения), аналогичной той, что проходят образцы при процедуре обработки реальных томограмм. Исходное разрешение реконструированного куба размером 400×400×400 вокселей, которое затем уменьшается в 2 раза, до значения 200×200×200 вокселей, путем усреднения значений рентгеновской плотности (plrescale) по группам из 8 вокселей (рис. 7).
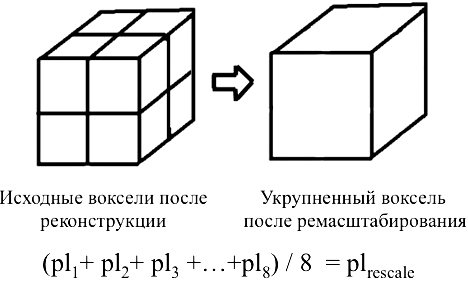
Рис. 7. Схема усреднения вокселей объемного изображения: pl1 – значение условной рентгеновской плотности исходного вокселя после реконструкции; plrescale – усредненное значении условной рентгеновской плотности укрупненного вокселя после ремасштабирования
Такая последовательность действий приближает вычислительный эксперимент к реальным алгоритмам работы со съемками керна горных пород. Но для корректности дальнейших сопоставлений кубов реконструированный куб размером 200×200×200 вокселей приводится к разрешению 400×400×400 вокселей, путем присваивания значений усредненной плотности (plrescale) группам из 8 вокселей (2×2×2). Такой переход (рис. 4в, 5в) позволяет проводить повоксельные сопоставления условной рентгеновской плотности вокселя начального куба и ремасштабированного реконструированного куба.
Контроль корректности вычислительного эксперимента производился путем построения корреляционных полей статистических характеристик условной рентгеновской плотности получаемых ремасштабированных кубов с характеристиками реальных съемок (рис. 8), на которых видно пересечение облаков точек.
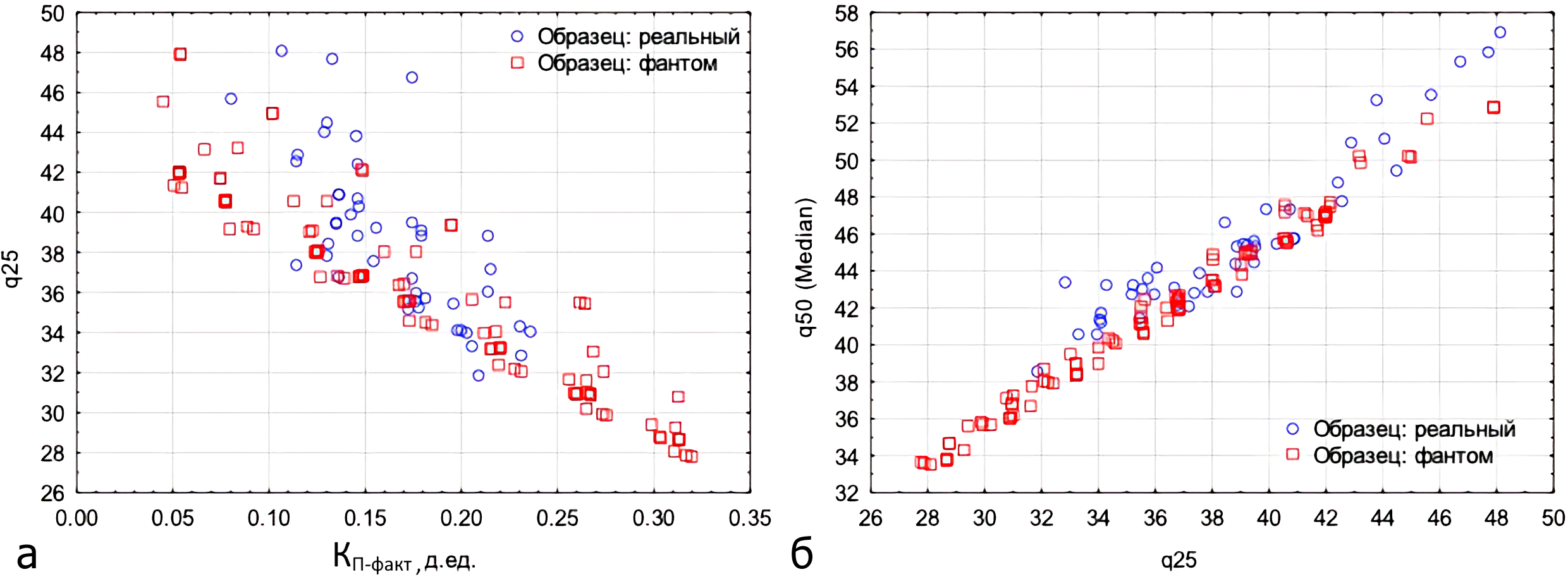
Рис. 8. Сопоставления статистических характеристик распределений условной рентгеновской плотности цифровых фантомов и реальных образцов: а) корреляционное поле между квантилем q25 и КП-факт; б) корреляционное поле между медианным значением (квантиль q50) и квантилем q25
Этап 6. После выполнения всех расчетов по полученным кубам строились гистограммы значений рентгеновской плотности в пределах самого образца (рис. 4) и раздельно для порового пространства и скелета фантома (рис. 9).
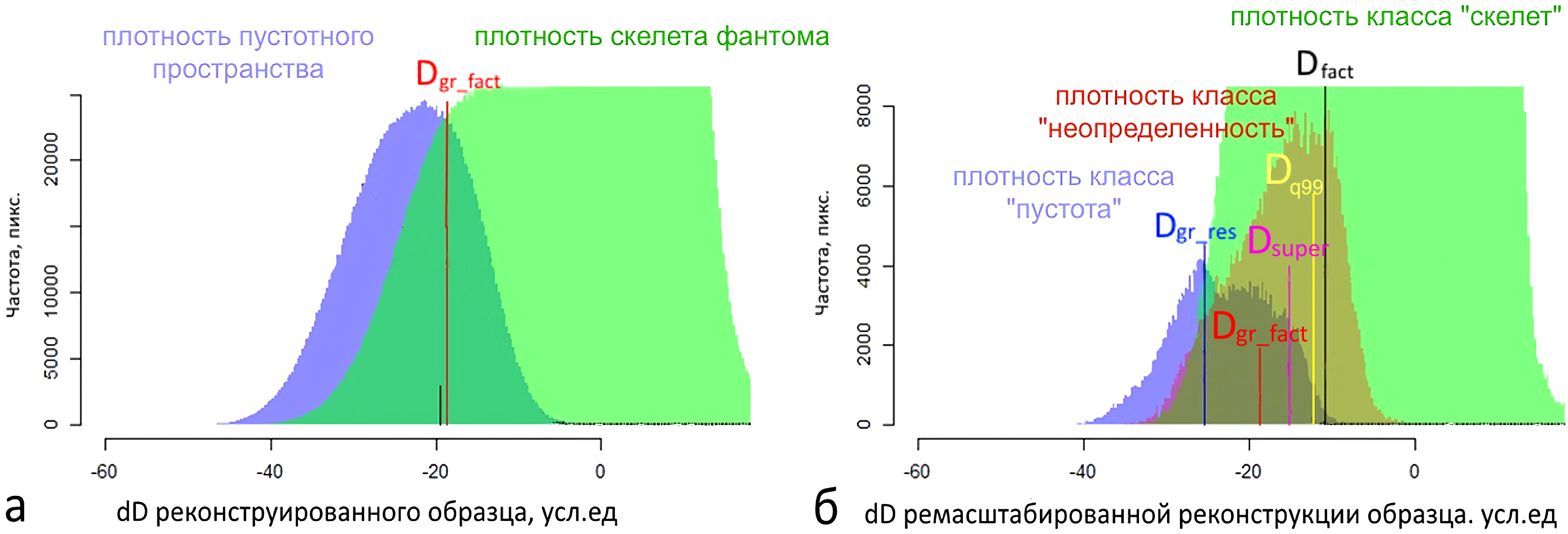
Рис. 9. Гистограммы dD ( КП-факт = 0,125 д.ед.). Расшифровка выделенных граничных значений в тексте: а) образец после реконструкции: зеленая область – плотность, соответствующая скелету фантома, синяя – плотность, соответствующая пустотному пространству фантома; б) образец после ремасштабирования: зеленая область – плотность класса «скелет», синяя – плотность класса «пустота», красная – плотность класса «неопределенность». Dgr_fact – значение dD рентгеновской плотности, приходящееся на пересечение гистограмм распределений пор и скелета по реконструированному образцу. Dsuper – медианное значение dD рентгеновской плотности класса «неопределенность»; Dgr_res – значение dD рентгеновской плотности, приходящееся на пересечение гистограмм распределений классов «пустота» и «скелет»; Dq – квантили 75, 80, 90, 95, 99% в распределении класса «пустота» dD ремасштабированного куба (Dq75, Dq80, Dq90, Dq95, Dq99); Dfact – граничное значение dD условной рентгеновской плотности образца, обеспечивающее фактическое значение КП-факт фантома.
Этап 7. По гистограммам значений рентгеновской плотности рассчитывались основные статистические характеристики (среднее значение, среднеквадратическое отклонение, коэффициенты асимметрии и эксцесса и др.) для разработки модели прогноза граничного значения пора – скелет.
Используя данный алгоритм, сгенерировано и проанализировано 124 фантома, имитирующих различную структуру порового пространства и различный минеральный состав реальных горных пород. Такие фантомы могут служить достоверной основой для сопоставления значений условной рентгеновской плотности в кубе исходного фантома и в реконструированном кубе после ремасштабирования.
Анализ результатов
Пустотное пространство ремасштабированного куба реконструкции можно расклассифицировать на группы, используя значения пористости укрупненного вокселя как отношение пустот (количество пустых вокселей) к объему укрупненного вокселя (равного 8 исходным вокселям).
Оценка пористости укрупненного вокселя проводилась согласно классификации укрупненных вокселей по трем классам: класс «пустота», где объем пустот в укрупненном вокселе > 0,5 д.ед; класс «неопределенность», где объем пустот в укрупненном вокселе = 0,5 д.ед.; класс «скелет», где объем пустот в укрупненном вокселе < 0,5 д.ед. После выполнения всех расчетов по полученным кубам строились гистограммы значений рентгеновской плотности в пределах самого образца, и рассчитывались основные статистические характеристики.
В дальнейших расчетах используется разность (dD) между исходным значением плотности в каждом вокселе (Di) и медианой рентгеновской плотности образца (Dn) ремасштабированного куба:
dD = Di – Dn. (1)
Такой подход позволяет избежать оценок граничных значений в абсолютной шкале условной рентгеновской плотности, и перейти к оценке положения различных рассматриваемых вариантов граничных значений относительно положения моды, как наиболее устойчивой статистической оценке куба условной рентгеновской плотности образца после реконструкции и после ремасштабирования.
На рис. 9 приведены гистограммы dD. С использованием гистограмм dD для скелета и пустотного пространства образца, определялись наиболее оптимальные граничные значения (отсечки) для оценки КП фантома.
Для реконструкции рассчитывалось Dgr_fact – значение dD рентгеновской плотности, приходящееся на пересечение гистограмм распределений пор и скелета по реконструированному образцу.
Для ремасштабированной модели цилиндрического образца рассчитывались:
Dsuper – медианное значение dD рентгеновской плотности класса «неопределенность»;
Dgr_res – значение dD рентгеновской плотности, приходящееся на пересечение гистограмм распределений классов «пустота» и «скелет»;
Dq – квантили 75, 80, 90, 95, 99% в распределении класса «пустота» dD ремасштабированного куба (Dq75, Dq80, Dq90, Dq95, Dq99);
Dfact – граничное значение dD условной рентгеновской плотности образца, обеспечивающее фактическое значение КП-факт фантома.
Полученные границы обеспечивают различную достоверность оценки условной рентгеновской плотности вокселя, соответствующего поре, в пределах образца породы. Для обоснования наиболее достоверной численной границы, обеспечивающей фактическое значения КП исходного фантома, производилось сопоставление значений пористости при использовании выделяемых отсечек (рис. 10).

Рис. 10. Корреляционное поле между КП-факт и а) значениями КП по квантилям (80%, 95%, 99%) в распределении пустота; б) значениями КП по пересечению гистограмм «скелет», «пустота» (КП_gr_rec), значениями КП по медиане класса «неопределенность» (КП_super)
Применение квантилей для отсечек характеризуется большей линейностью зависимости прогноз – факт, но при этом для высоких значений КП прогнозные значения имеют более широкий интервал варьирования. Отсечка в виде пересечения гистограмм классов «скелет» – «пустота» (Dgr_rec) существенно занижает прогнозные значения и обладает выраженной нелинейностью. Медиана класса «неопределенность» (Dsuper) ведет себя аналогично, но еще сильнее занижает значения КП.
Построение корреляционных полей и проведенный анализ регрессионных зависимостей КП-прогноз – КП-факт, получаемых при разных отсечках, позволили установить, что наилучшей прогнозной характеристикой граничного значения является 99% квантиль в распределении «пустота» (Dq99) (рис. 8), что подтверждается наиболее приближенным к единице угловым коэффициентом в регрессионной зависимости и высоким значением парного коэффициента корреляции r = 0,963 при достигаемом уровне значимости p < 10-5.
С помощью пошагового регрессионного анализа на 124 фантомах, имитирующих структуру порового пространства, установлена следующая модель прогноза граничного значения dD условной рентгеновской плотности, соответствующей границе пора – скелет (Савицкий, 2023):
Dq99 = –34,99 + 50,96 × (КПГАЗ)2 + 2,34 × (q50/(q50 – q25)) – 1,29×Ek –2,79 × (Mean/SD) – 7,21 × lg(КПГАЗ),
(R2 = 0,974, скоррект. R2 = 0,972), (2)
где КПГАЗ – значение пористости образца газоволюметрическим методом (д.ед.); Ek – эксцесс образца; Mean – среднеарифметическое значение условной рентгеновской плотности ремасштабированного куба в пределах цилиндрического образца (усл.ед.); SD – среднеквадратическое отклонение условной рентгеновской плотности ремасштабированного куба в пределах цилиндрического образца (усл.ед.). Значение Dq99 показывает отклонение от медианы условной рентгеновской плотности (dD) реконструированного образца после ремасштабирования.
Модель прогноза специально создавалась на характеристиках, не привязанных к абсолютным значениям рентгеновской плотности, т.к. измеряемые значения поглощения рентгеновского излучения могут меняться со временем (из-за изменения параметров источника, смены нитей накала, деградации детектора, и т. д.). При этом процедура калибровки томографа может вносить существенную систематическую погрешность. Использование значения КПГАЗ объясняется тем, что КПГАЗ входит в стандартные исследования керна, и эта величина определяется в подавляющем большинстве случаев для образцов 30-миллиметрового керна.
При помощи зависимости 2 можно оценить значение отсечки Dq99, обеспечивающей выделение и визуализацию наиболее достоверно существующего пустотного пространства в ремасштабированном кубе.
Разработанная модель прогноза граничного значения проверена на 46 реальных образцах керна, которые не привлекались для создания этой модели прогноза. Применение предложенной модели прогноза значения отсечки на реальных томограммах керна пород-коллекторов показало высокую степень соответствия фактическим данным (рис. 11).
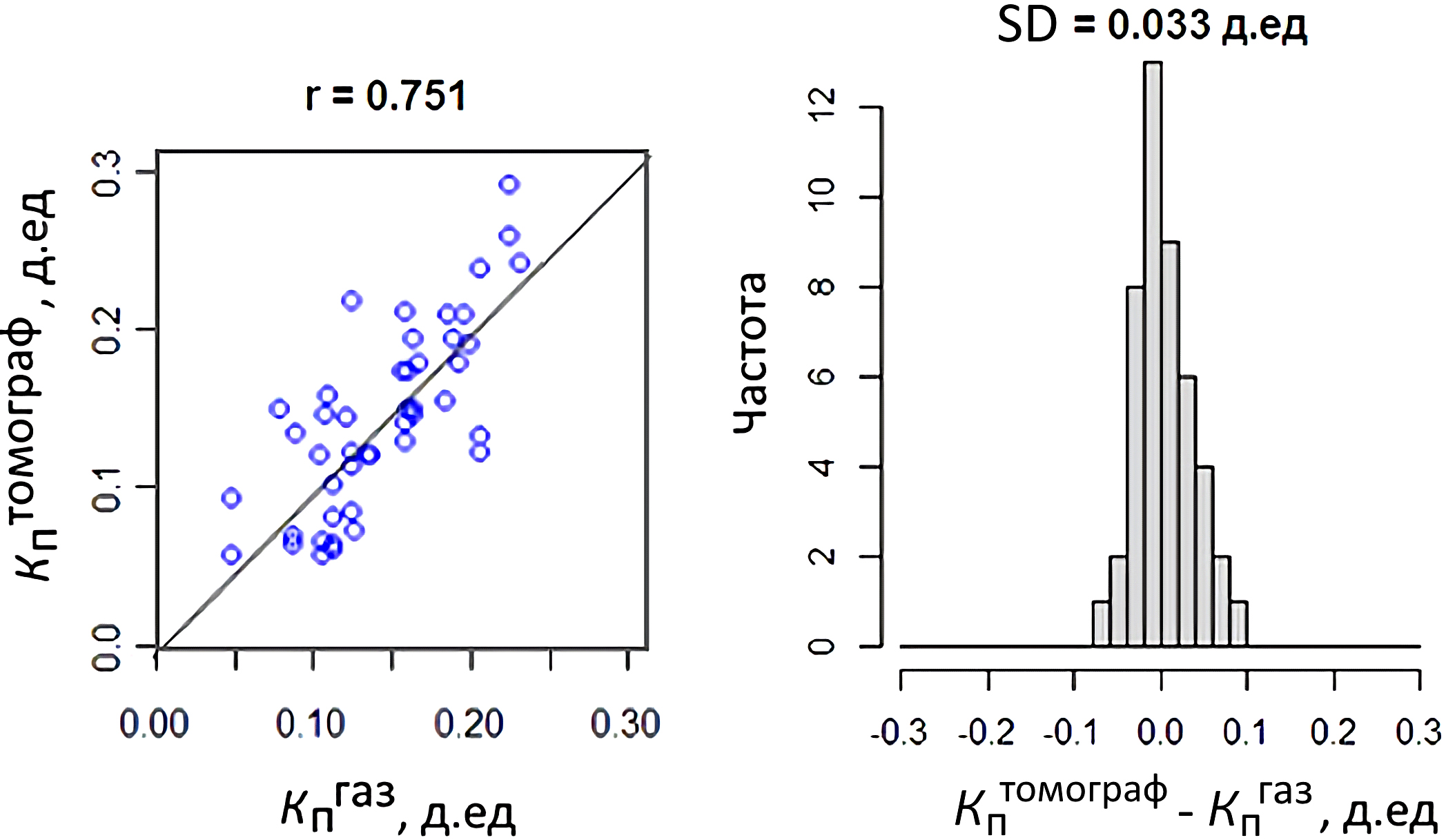
Рис. 11. Проверка зависимости на 46 моделях реальных образцов: r – коэффициент корреляции, SD – среднеквадратическое отклонение разности Кптомограф – КПГАЗ, Кптомограф – значение пористости по предложенной методике, д.ед., Кпгаз – значение пористости, измеренное методом газоволюметрии, д.ед., Кптомограф – КПГАЗ – разность между прогнозными (томография) и фактическими (газоволюметрия) Кп
Удовлетворительная сходимость оценок КП получена даже несмотря на различие алгоритмов реконструкции вычислительного эксперимента на фантомах (реконструкция FDK с использованием библиотеки ASTRA v2.1.0) и реконструкции реальных данных в проприетарном ПО томографа (Nikon Metrology CT Pro 3D).
При помощи данной модели можно оценить значение отсечки Dq99, обеспечивающей выделение наиболее достоверно существующего пустотного пространства в ремасштабированном кубе.
На основе полученных результатов можно рекомендовать следующий алгоритм получения граничного значения при томографических исследованиях керна:
1) исследование пористости образца газоволюметрическим методом и определение значения КП по газу (КПГАЗ);
2) проведение компьютерной рентгеновской томографии образца и его реконструкция;
3) получение граничного значения Dq99 по зависимости (2).
После этого возможна визуализация и расчеты морфологических характеристик пустотного пространства в объеме образца.
Заключение
По результатам анализа томограмм керна реальных терригенных пород коллекторов стандартного размера, установлена невозможность «прямого» решения задачи определения граничного значения (отсечки) условной рентгеновской плотности для оценки КП. С учетом этого предложен методический подход, основанный на применении цифровых фантомов керна с известными характеристиками пустотного пространства. Разработан план вычислительного эксперимента, и представлена его реализация в виде компьютерной программы (кода) на языке программирования Python. Реализованный подход позволяет оценивать влияние пористости и ее структуры на распределение условной рентгеновской плотности и представляется авторам перспективным методом вычислительной проверки результатов рентгеновской томографии. На основании вычислительного эксперимента, по данным 124 цифровых фантомов, обоснована методика оценки оптимизации граничного значения условной рентгеновской плотности. При этом получена модель прогноза, основанная на относительных статистических характеристиках гистограммы образца в реконструированном кубе. Применение относительных величин позволяет уйти от проблем калибровки оборудования.
Данная модель прогноза граничного значения проверена на 46 съемках реального керна (не использовавшихся для разработки модели) и показала хорошие статистические характеристики между фактическими и прогнозными значениями КП: коэффициент корреляции r между прогнозными и фактическими значениями КП составил 0,751, среднеквадратическое отклонение – sd = 0,033 д.ед. Такие характеристики позволяют использовать ее при интерпретации результатов рентгеновской томографии керна стандартного размера для выделения и визуализации наиболее достоверных пустот.
Дальнейшее развитие методики прогноза связано с увеличением размерности моделей фантомов, что требует значительно больших вычислительных мощностей как на этапе создания, так и на этапе реконструкции фантомов, а также совершенствование этапа генерации структуры пустотного пространства фантома и его минералогических неоднородностей, для более достоверного воспроизведения пустотного пространства горных пород.
Финансирование/Благодарности
Исследования выполнены при поддержке Министерства науки и высшего образования Российской Федерации (проект № FSNM-2023-0005).
Работы выполнены на оборудовании Центра фильтрационно-емкостных свойств горных пород ПНИПУ и Уникальной научной установке «Комплекс для исследования структуры емкостного пространства горных пород».
Авторы благодарят рецензентов за ценные замечания, способствующие улучшению работы.
1. Filtered Back Projection – фильтрованная обратная проекция
2. Simultaneous Iterative Reconstruction Technique метод одновременной итерационной реконструкции
3. Simultaneous Algebraic Reconstruction Technique метод одновременной алгебраической реконструкции
4. Conjugate Gradient Least Squares – метод наименьших квадратов сопряженного градиента
5. Algebraic Reconstruction Technique – метод алгебраической реконструкции
Список литературы
1. Галкин С.В., Кетова Ю.А., Савицкий Я.В., Кинг В., Бауыржан С. (2020). Изучение механизма перераспределения фильтрационных потоков при закачке синтезированных сшитых гелей методом рентгеновской томографии керна. Известия Томского политехнического университета. Инжиниринг георесурсов, 331(11), c. 127–136. https://doi.org/10.18799/24131830/2020/11/2892
2. Дмитриева, А. Ю. Мусабиров И. М., Насибулин М. Х. (2018). Исследование влияния химических обрабатывающих составов на кольматационные процессы и изменение фильтрационно-емкостных свойств кернового материала тульско-бобриковского горизонта Экспозиция Нефть Газ, 4(64), с. 38–42.
3. Еременко Н.М., Муравьева Ю.А. (2012). Применение методов рентгеновской микротомографии для определения пористости в керне скважин. Нефтегазовая геология. Теория и практика, 7(3). http://www. ngtp.ru/rub/2/35_2012.pdf
4. Кривощёков С.Н., Кочнев А.А. (2013). Опыт применения рентгеновской компьютерной томографии для изучения свойств горных пород. Вестник ПНИПУ. Геология. Нефтегазовое и горное дело, (6), c. 32–42. https://doi.org/10.15593/2224-9923/2013.6.4
5. Мартюшев, Д. А. Новиков В. А. (2020). совершенствование кислотных обработок в коллекторах, характеризующихся различной карбонатностью (на примере нефтяных месторождений Пермского края) Известия Томского политехнического университета. Инжиниринг георесурсов, 331(9), с. 7–17. https://doi.org/10.18799/24131830/2020/9/2800
6. Осовецкий Б.М., Казымов К.П., Колычев И.Ю., Савицкий Я.В., Галкин С.В. (2023). Изучение изменений структуры пустотности горных пород при создании напряженного состояния методами электронной микроскопии Георесурсы, 25(2), с. 228–235. https://doi.org/10.18599/grs.2023.2.16
7. Савицкий Я.В., (2023). Изучение особенностей структуры пустотного пространства коллекторов методом рентгеновской томографии керна. Автореф. дис. кан. тех. наук., 22 с.
8. Савицкий Я.В., Галкин С.В. (2021). Применение процедуры трешхолдинга при изучении емкостного пространства горных пород методом рентгеновской томографии. Горный журнал, 7(2288), с. 34–39.
9. Чистяков А.А., Швалюк Е.В., Калугин А.А. (2022). Применение компьютерной томографии и ямр для петротипизации сложнопостроенных терригенных коллекторов. Георесурсы, 24(4), с. 102–116. https://doi.org/10.18599/grs.2022.4.9
10. Чугунов С.С. Казак А.В., Черемисин А.Н. (2015). Комплексирование методов рентгеновской микротомографии и трёхмерной электронной микроскопии при исследовании пород баженовской свиты Западной Сибири. Нефтяное хозяйство. (10). c. 44–49.
11. Abella M., Vaquero J. J., Sisniega A. et al. (2012) Software architecture for multi-bed FDK-based reconstruction in X-ray CT scanners. Computer Methods and Programs in Biomedicine, 7(2), pp. 218–232. https://doi.org/10.1016/j.cmpb.2011.06.008
12. Chukalina M., Khafizov A., Kokhan V., Buzmakov A., Senin R., Uvarov V., Grigoriev M. (2021). Algorithm for post-processing of tomography images to calculate the dimension-geometric features of porous structures. Computer Optics, 45, pp. 110–121. https://doi.org/10.18287/2412-6179-CO-781
13. Denney D. (2004). Digital Core Laboratory: Reservoir-Core Properties Derived From 3D Images. Journal of Petroleum Technology, 56(05), pp. 66–88. https://doi.org/10.2118/0504-0066-JPT
14. Djimasbe R., Varfolomeev M.A., Kadyrov R.I., Davletshin R.R., Khasanova N. M., Saar F.D., Ameen A., Muneer A.S, Mukhamedyarova A. N., (2022). Intensification of hydrothermal treatment process of oil shale in the supercritical water using hydrogen donor solvents. The Journal of Supercritical Fluids, (191), 105764. https://doi.org/10.1016/j.supflu.2022.105764
15. Eric J. Goldfarb, Ken Ikeda, Richard A. Ketcham, Maša Prodanović, Nicola Tisato (2022). Predictive digital rock physics without segmentation, Computers & Geosciences, (159), 105008. https://doi.org/10.1016/j.cageo.2021.105008
16. Feldkamp L.A., Davis L. C., Kress J.W. (1984). Practical cone-beam algorithm, J. Opt. Soc. Am. A 1, pp. 612–619. https://doi.org/10.1364/JOSAA.1.000612
17. Fernandes J.S. Appoloni C.R. Fernandes C.P. (2012). Determination of the Representative Elementary Volume for the Study of Sandstones and Siltstones by X-Ray Microtomography, Materials Research, 15(4), pp. 662–670.
18. Galkin S., Savitsky Y., Shustov D., Kukhtinskii A., Osovetsky B. et al. (2023). Modeling of Crack Development Associated with Proppant Hydraulic Fracturing in a Clay-Carbonate Oil Deposit. FDMP-Fluid Dynamics &Materials Processing, 19(2), pp. 273–284. https://doi.org/10.32604/fdmp.2022.021697
19. Hamed Lamei Ramandi, Muhammad Asad Pirzada, Serkan Saydam, Christoph Arns, Hamid Roshan (2021). Digital and experimental rock analysis of proppant injection into naturally fractured coal. Fuel, (286), Part 1, 119368. https://doi.org/10.1016/j.fuel.2020.119368
20. Hounsfield G.N. (1973). Computerized transverse axia scanning (tomography). Part 1: Description of system. British Journal of Radiology, (46), pp. 1016–1022. https://doi.org/10.1259/0007-1285-46-552-1016
21. Jamie Lea Pointon, Tianci Wen, Jenna Tugwell-Allsup, Aaron Sújar , Jean Michel Létang, Franck Patrick Vidal (2023). Simulation of X-ray projections on GPU: Benchmarking gVirtualXray with clinically realistic phantoms. Computer Methods and Programs in Biomedicine, (234), 107500. https://doi.org/10.1016/j.cmpb.2023.107500
22. Jun Feng, Jian-Zhou Zhang, Bin Zhou (2013). A novel kernel-based limited-view computerized tomography reconstruction via anisotropic diffusion. Computers & Electrical Engineering, 39(1), pp. 89–102. https://doi.org/10.1016/j.compeleceng.2012.10.014
23. Katsevich A. (2004). An improved exact filtered backprojection algorithm for spiral computed tomography. Advances in Applied Mathematics, (32), pp. 681–697. https://doi.org/10.1016/S0196-8858(03)00099-X
24. Ketcham R.A., Hanna R.D. (2014). Beam hardening correction for X-ray computed tomography of heterogeneous natural materials. Computers & Geosciences, (67), pp. 49–61. https://doi.org/10.1016/j.cageo.2014.03.003
25. Kingston A., Myers G., Latham S., Recur B., Li Heyang, Sheppard A. (2018). Space-Filling X-Ray Source Trajectories for Efficient Scanning in Large-Angle Cone-Beam Computed Tomography. IEEE Transactions on Computational Imaging, pp. 1–1. https://doi.org/10.1109/TCI.2018.2841202
26. Manazael Zuliani Jora, Renato Nunes de Souza, Everton Lucas-Oliveira, Carlos Speglich, Tito José Bonagamba, Edvaldo Sabadini (2021). Static acid dissolution of carbonate outcrops investigated by 1H NMR and X-ray tomography. Journal of Petroleum Science and Engineering, (207), 109124. https://doi.org/10.1016/j.petrol.2021.109124
27. Manu K. Mohan, A.V. Rahul, Jeroen F. Van Stappen, Veerle Cnudde, Geert De Schutter, Kim Van Tittelboom (2023). Assessment of pore structure characteristics and tortuosity of 3D printed concrete using mercury intrusion porosimetry and X-ray tomography. Cement and Concrete Composites, (140), 105104. https://doi.org/10.1016/j.cemconcomp.2023.105104
28. Marco Voltolini, Jonny Rutqvist, Timothy Kneafsey (2021). Coupling dynamic in situ X-ray micro-imaging and indentation: A novel approach to evaluate micromechanics applied to oil shale. Fuel, (300), 120987. https://doi.org/10.1016/j.fuel.2021.120987
29. Prasad S.K., Sangwai J.S., Byun H.-S. (2023). A review of the supercritical CO2 fluid applications for improved oil and gas production and associated carbon storage. Journal of CO2 Utilization, (72), 102479. https://doi.org/10.1016/j.jcou.2023.102479
30. Romano C., Minto J.M., Shipton Z K., Lunn R.J. (2019) Automated high accuracy, rapid beam hardening correction in X-Ray Computed Tomography of multi-mineral, heterogeneous core samples. Computers & Geosciences, (131), pp. 144–157. https://doi.org/10.1016/j.cageo.2019.06.009.
31. Shah S., Yang, J., Crawshaw J., Gharbi O., Boek E. (2013). Predicting Porosity and Permeability of Carbonate Rocks From Core-Scale to PoreScale Using Medical CT Confocal Laser Scanning Microscopy and Micro CT. Proceedings SPE Annual Technical Conference and Exhibition, (3). https://doi.org/10.2118/166252-MS
32. Shameem Siddiqui, Hisham A. Nasr-El-Din, Aon A. Khamees (2006). Wormhole initiation and propagation of emulsified acid in carbonate cores using computerized tomography. Journal of Petroleum Science and Engineering, 54(3–4), pp. 93–111. https://doi.org/10.1016/j.petrol.2006.08.005
33. Soimu D., Buliev I., Pallikarakis N. (2008). Studies on circular isocentric cone-beam trajectories for 3D image reconstructions using FDK algorithm. Computerized Medical Imaging and Graphics, 32(3), pp. 210–220. https://doi.org/10.1016/j.compmedimag.2007.12.005
34. Van Aarle W., Palenstijn W. J., Cant J., Janssens E., Bleichrodt F., Dabravolski A., De Beenhouwer J., Batenburg K.J., Sijbers J. (2016). Fast and Flexible X-ray Tomography Using the ASTRA Toolbox. Optics Express, 24(22), pp. 25129–25147. https://doi.org/10.1364/OE.24.025129
35. Van Aarle W., Palenstijn W.J.A., De Beenhouwer J., Altantzis T., Bals S., Batenburg K.J., Sijbers J. (2015). The ASTRA Toolbox: A platform for advanced algorithm development in electron tomography. Ultramicroscopy, (157), pp. 35–47. https://doi.org/10.1016/j.ultramic.2015.05.002
36. Vinegar H.J. (1986). X-ray CT and NMR imaging of rocks. Journal of Petroleum Technology, (38), pp. 257–259. https://doi.org/10.2118/15277-PA
37. Wenxuan Liang, Hui Zhang, Guangshu Hu (2010). Optimized Implementation of the FDK Algorithm on One Digital Signal Processor Tsinghua Science & Technology, 15(1). pp. 108–113. https://doi.org/10.1016/S1007-0214(10)70017-1
Об авторах
О. А. МелкишевРоссия
Олег Александрович Мелкишев – доцент кафедры Геология нефти и газа, кандидат техн. Наук.
614990, Пермь, Комсомольский пр., д. 29
Я. В. Савицкий
Россия
Ян Владимирович Савицкий – инженер кафедры Геология нефти и газа, кандидат тех. наук.
614990, Пермь, Комсомольский пр., д. 29
С. В. Галкин
Россия
Сергей Владиславович Галкин – доктор геол.-минерал. наук, профессор, декан горно-нефтяного факультета.
614990, Пермь, Комсомольский пр., д. 29
Рецензия
Для цитирования:
Мелкишев О.А., Савицкий Я.В., Галкин С.В. Применение искусственных цифровых моделей в методе рентгеновской томографии керна при решении задачи бинаризации пустотного пространства горных пород. Георесурсы. 2024;26(4):218-228. https://doi.org/10.18599/grs.2024.4.11
For citation:
Melkishev O.A., Savitsky Y.V., Galkin S.V. The Application of Artificial Digital Models in X-Ray Computed Tomography (CT) of the Core in Solving the Problem of Binarization of the Void Space of Reservoir Rocks. Georesursy = Georesources. 2024;26(4):218-228. (In Russ.) https://doi.org/10.18599/grs.2024.4.11















.png)


